[시각지능] Projective geometry

Projective geometry

Projective geometry는 image transformatin을 modeling하는 방법 중 하나인데, 이 방법이 기존의 2D transformation 방법과 어떻게 다른지 알아보고자 한다.

Homogeneous coordinates

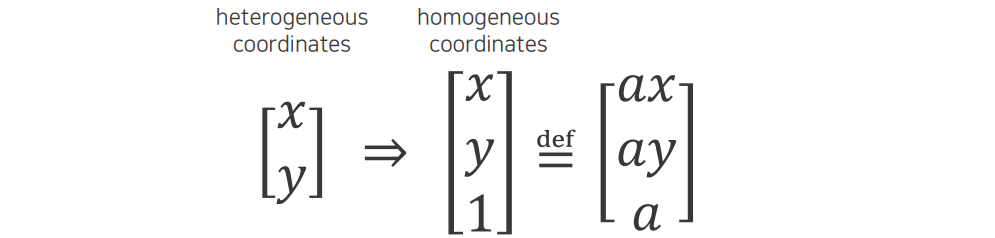2D transformation을 modeling하기 전에 homogeneous coordinate에 대해서 먼저 알아야 한다. 기존의 heterogeneous coordinate에서는 2D point를 $x,y$를 통해서 vector로 표현할 수 있었다. 이때, 여기에 1을 추가하여 3D vector로 만들어 2D vector를 표현하는 것이 homogeneous coordinate를 표현하는 방식이다. Homogeneous coordinate의 특징은 scale을 곱한 것과 곱하지 않은 것이 같다는 것이다. 그래서 scale-invariant한 특징을 가지게 되어 어떠한 scale을 곱해도 상관이 없다.

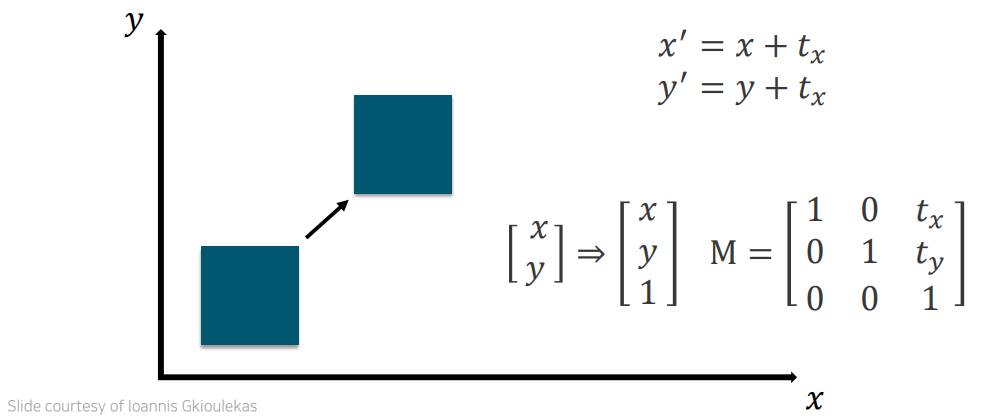이전에 2D translation의 경우에는 $2\times2$ matrix로 표현이 불가능했다. 여기서 homogeneous coordinate를 사용하지 않고 heterogeneous coordinate를 사용하면 matrix 형태로 표현이 불가능했었다. 하지만 homogeneous coordinate로 표현을 바꿔주게 되면 우리는 matrix 형태로도 표현이 가능해진다. 2차원에서는 표현이 불가능했지만, 이를 3차원으로 좌표만 바꿔주게 되면 표현이 가능해진다.

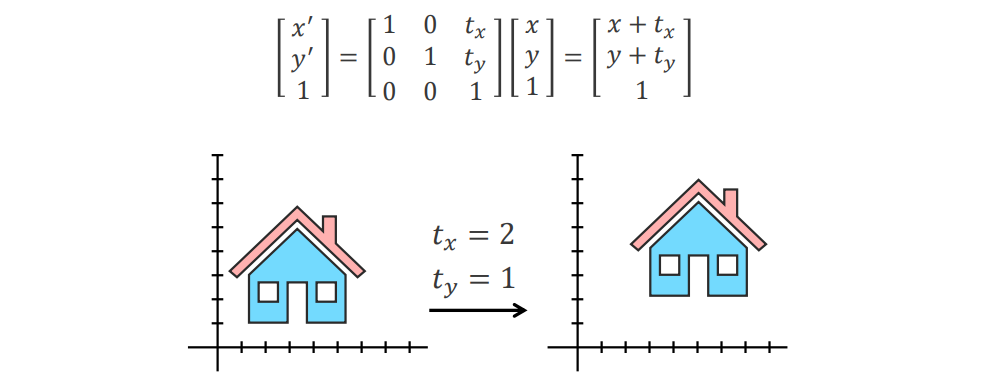그래서 homogeneous coordinate를 사용하게 되면 위와 같이 matrix 형태로 하나로 표현이 가능해져 간단해진다.

Homogeneous coordinate는 다양한 성질들을 가지고 있다. 우리가 heteroneneous coordinate에 1을 추가해서 homogeneous coordinate로 변환이 가능했었다. 이를 반대로 변환하고자 한다면 마지막에 추가된 값으로 normalization을 해주어 heterogeneous coordinate로 다시 변환이 가능해진다. 우리는 항상 마지막에 1이 존재한다고 가정하기 때문에 scale invariance 성질도 정의가 되는 것이다.

더불어 마지막에 1이 아니라 0인 경우에는 point at infinity라고 해서 infinity point를 표현할 수 있게 된다. 사실 infinity라는 것은 무한대로 어떻게보면 방향성이 존재하지 않는다. 결국 $x,y$ 모두 infinity가 되는 셈인데, 이를 homogeneous coordinate로 표현해서 끝을 0으로 두고 나머지 부분에 방향성 vector를 삽입을 하게 되면 무한대임에도 불구하고 방향성을 가지는 vector를 표현할 수 있게 된다. 마찬가지로 normalization을 하게 되면 실제로 정의는 되지 않지만, 굉장히 작은 값을 의미하게 되어 무한대와 동일한 형태가 되어 heterogeneous와 homogeneous 사이의 관계에서 homogeneous coordinate가 infinity point에 대해서 더 많은 정보를 표현할 수 있는 장점을 가지게 된다. 이는 차원을 하나 추가했기 때문에 더 표현력이 좋아졌다라고 볼 수 있는 것이다. 이때, 모든 값이 0이 되면 undefined로 정의하게 되는 것이다.

Projective geometry

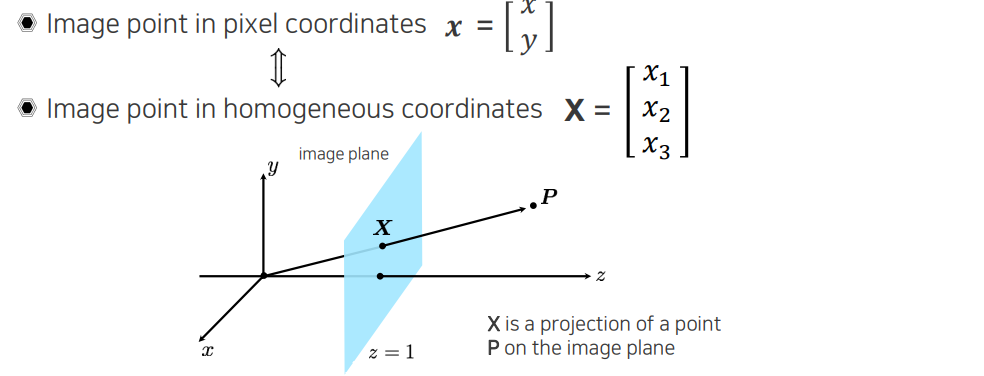Projective geometry는 카메라의 위치에 따라 plane의 관계를 나타낸다고 볼 수 있었다. 그래서 우리는 image plane 상에서 pixel을 heterogeneous coordinate로 표현할 수 있는데, 이를 homogeneous coordinate로 차원을 늘려서 표현할 수도 있게 된다. 그리고 위와 같은 coordinate system이 존재할 때, 카메라의 image plane을 가정한다는 것은 homogeneous coordinate 마지막에 1을 삽입하는 것과 같다. 이를 통해서 일종의 정규화 된 카메라를 정의했다고 봐도 된다. 그래서 어떠한 point $P$가 image plane에 projection 되는 것은 원점에서부터 $P$까지 이어주는 선과의 교점으로 존재하게 될 것이다. 여기서 $P$와 projection point $X$ 사이의 관계를 modeling하는 것을 projective geometry라고 한다.

Transformations in projective geometry

이제 projective geometry 관점에서 2D transformation들에 대해서 보고자 한다. 이전에 보았던 $2\times2$ matrix를 이제는 homogeneous coordinate를 활용해서 $3\times3$ matrix로 바꿔주고자 한다. 이러한 과정에서 무엇이 바뀌는지를 중심으로 알아야 한다.
위의 matrix들을 보면 기존의 $x,y$에 해당되는 $2\times2$ matrix가 좌측 상단에 그대로 들어가는 것을 확인할 수 있다. 그리고 추가적으로 translation과 관련된 정보는 우측 상단에 반영되고 있다.

Matrix composition

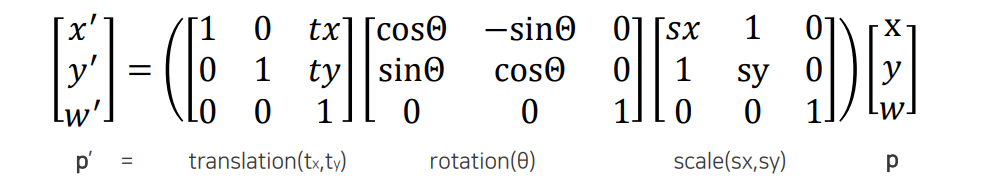여기서 우리가 궁금한 것은 여러가지 transformation을 동시에 반영할 수 있는지이다. 위와 같이 scaling, rotation, translation을 차례로 반영시킬 수 있다. 이러한 transformation을 동시에 반영시켜 하나의 $3\times3$ matrix로 표현할 수 있는 것이 homogeneous coordinate의 또 다른 장점이 된다. 여기서 주의할 점은 순서를 잘 고려해서 반영해야 한다.

Classification of 2D transformations

Homogeneous coordinate를 통해서 2D transformation들을 어떻게 표현하는지 알아보았는데, 이번에는 이들의 parameter들에 대해서 살펴보고자 한다.

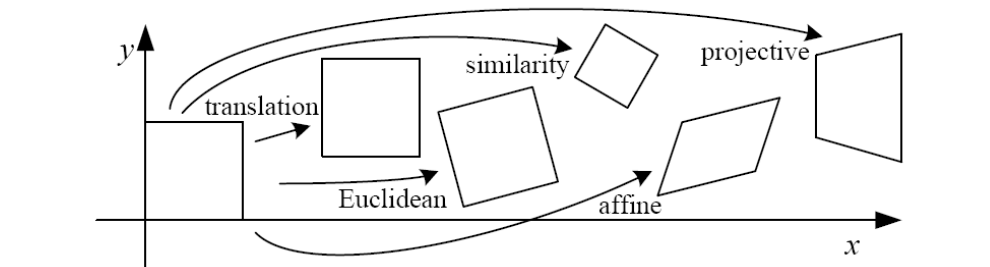이전에 보았듯이 trnaslation, similarity, Euclidean transofrmation 등의 관계성이 위와 같이 표현이 되어있는데, 여기서 오른쪽으로 갈수록 DOF가 높아졌다.

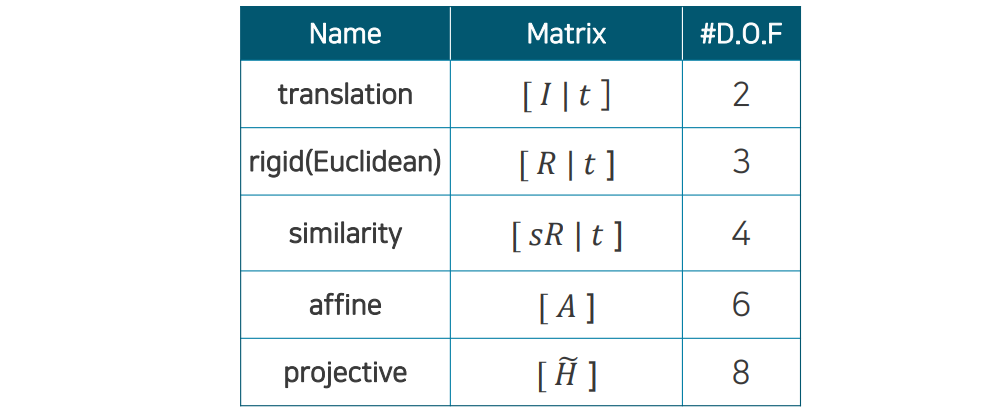이전과는 다르게 homogenous coordinate 상에서 $3\times3$ matrix를 위와 같이 사용할 수가 있다. 마찬가지로 projective transformation으로 갈수록 DOF가 높아지게 되어 다양한 형태로 변형이 가능해진다.

Translation

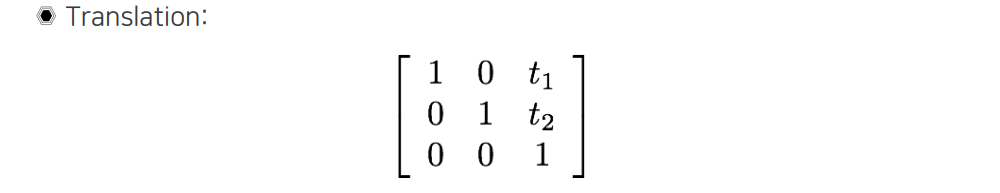처음으로 translation에는 unknown parameter가 총 2개가 존재한다. 우리는 2개의 값을 조절할 수 있기 때문에 DOF는 2가 되는 것이다.

Euclidean(rigid)

Euclidean transformation은 rotation과 translation을 동시에 할 수 있는 transformation으로 여기서 중요한 것은 scaling이 반영되지 않는다. 위에서 $r_3,r_6$는 translation에 영향을 줄 것이다.
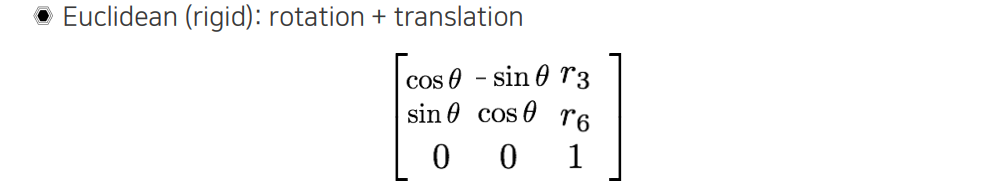나머지 $2\times2$ matrix는 rotation을 표현하게 된다. 여기서 DOF를 생각했을 때 어떻게 보면 총 6개라고 생각할 수 있지만, rotation은 $\theta$만을 통해서 각도를 조절할 수 있기 때문에 총 3이 되는 것이다

Similarity

우리가 Euclidean transformation에서 rotation에 해당하는 부분을 rotation이라고 생각하지 않게되면 이는 전체적으로 similarity transformation이 된다. Similarity transformation의 경우 Euclidean transformation에서 반영하지 않았던 scaling을 반영하게 된다.

Scaling을 반영한다고 하면 좌측 상단의 rotation 부분에 scale을 조절할 수 있는 $s$를 곱해주면 된다. 여기서 DOF는 기존의 3에서 scale을 추가했으므로 총 4가 될 것이다.

Affine

Affine transformation은 Similarity transformation에 shearing까지 포함한 것이다. 그래서 새로운 shearing parameter까지 포함하게 된다면 다음과 같이 조금 복잡한 형태가 될 것이다.

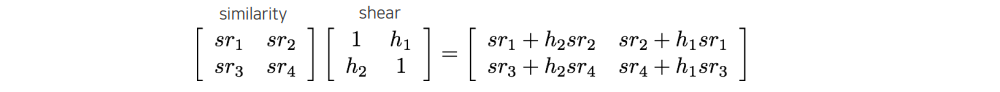Similarity transformation에서 shearing까지 들어가게 된다면 위와 같이 matrix가 표현이 되는데, 이 표현은 어떻게 보면 일반적으로 표현한 $2\times2$ matrix로 볼 수 있다. 그래서 어떠한 parameter의 제약이 없이 $2\times3$ matrix로 affine transformation을 표현할 수 있게 된다. 여기서 DOF는 그저 6개의 parameter를 조절할 수 있다고 보면 된다.

이번에는 affine transformation이 가지는 특징들을 조금 더 자세하게 보고자 한다. Affine transformation은 어떻게 보면 DOF가 4인 임의의 linear transformation과 translation을 결합한 것으로 볼 수가 있다. 그렇다면 여기서 linear하고 translation하고 분리시킨 이유는 무엇일까? 선형대수학에서 linear subspace의 정의를 보면 항상 origin을 포함해야 한다. 그렇기 때문에 translation 부분이 존재하지 않고, translation의 개념을 추가하게 되면 더이상 linear subspace라고 부르지 않게 된다. 그래서 우리는 이를 linear transformation이 아닌 affine transformation이라고 부르는 것이다.

Affine transformation은 origin이 반드시 origin으로 mapping이 되지 않고 offset이 존재해도 된다. 그리고 line이 curve가 되면 안되고, parralle line은 그대로 parralle line을 만족해야 한다. 또한 ratio도 바뀌지 않고 보존되어야 하며, affine을 여러번 적용해도 affine transformation으로 반드시 존재해야 한다. 마지막으로 마지막에 추가된 $w$는 바뀌지 않고 그대로 존재할 것이다.

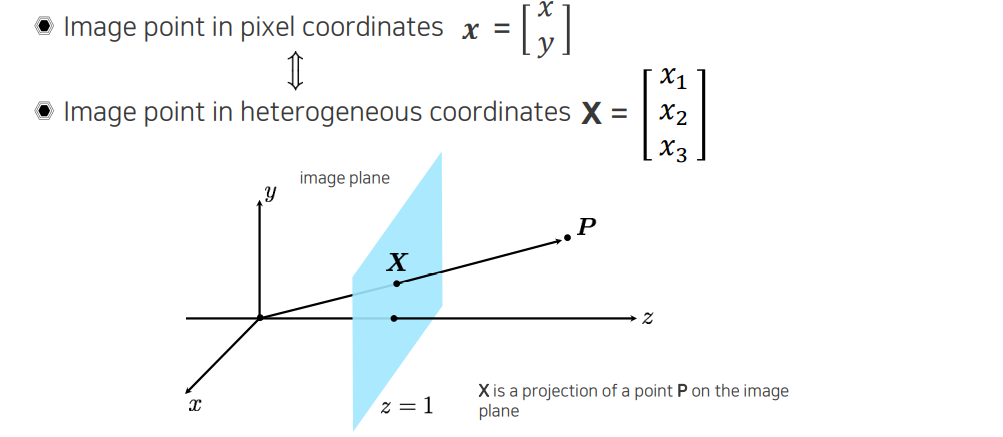여기서 바뀌지 않는 것에 대해서 의미를 생각해보고자 할 때, 다시 위와 같은 image plane 도식을 생각해보면 된다. Affine transformation에서 마지막 값은 1이고 어떠한 affine transformation을 하더라도 바뀌지 않는다는 것은 위에서 image plane이 다른 곳으로 도망가지 않는다는 것을 의미하게 된다. $P$가 어디에 위치하는지에 따라서 image plane 위에 존재하는 $X$만 이 plane 위에서 이동하게 될 것이다. 앞서 말한 affine transformatino의 성질들은 유지한 상태로 plane 상에서 이동만 할 것이다.

Projective

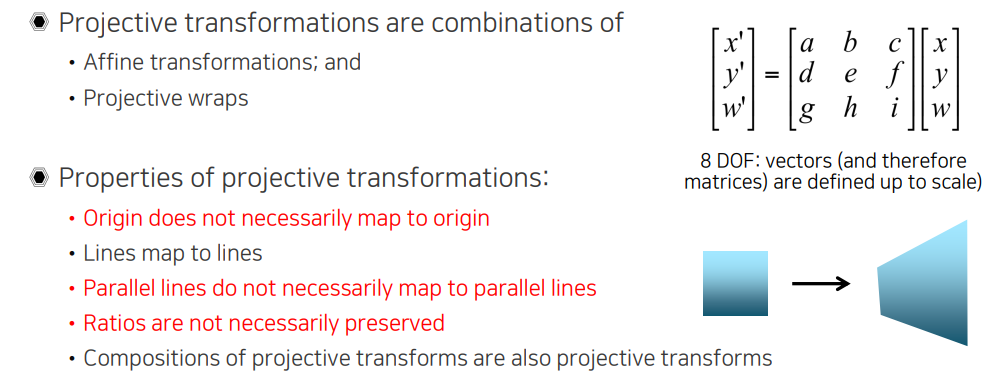Affine transformation에서 한단계 더 나아가면 더 자유로운 projective transformation 혹은 homography transformation이 존재한다. 여기서는 affine transformation 뿐만 아니라 projective warping이라는 개념이 들어간다. Projective warping이라는 것은 위에서 마지막 row에 해당하는 $g,h,i$ parameter를 말한다. 이 값들이 더이상 0, 0, 1이 아닌 상태가 된다. 기존의 affine transformation과 동일한 성질들을 기반으로 하지만, 다른 점으로는 더이상 parallel line이 그대로 존재하지 않으며 ratio 또한 보존되지 않아도 된다는 것이다. Projective transformation을 적용하고 다시 projective transformation을 적용한 결과가 있을 때, affine transformation과 마찬가지로 이를 표현할 수 있는 projective transformation 표현 하나가 존재하게 되어 해당 transformation에 대해서 닫힌 상태가 된다.

Projective transformation의 DOF는 8이다. 분명 parameter는 9개이지만 왜 8인지 생각해본다면, 이전에 homogeneous coordinate system을 사용하기 때문에 마지막 $w$에 대해서 scale-invariant한 성질을 가지고 있다. 그래서 scale에 상관이 없기 때문에 하나의 DOF가 빠질 수 있는 것이다.

Affine transformation과 마찬가지로 마지막 $w$에 대해서 생각해 본다면 마지막 row가 0,0,1이 아니기 때문에 더이상 $w$가 1이 아니더라도 그대로 존재할 수 없는 것이다. 3개의 entry 중에서 앞에 2개가 0이 아니기 때문에 $x,y$ 좌표에 따라서 $w$ 값이 바뀌게 된다. 그러면 affine transformation과는 다르게 projective transformation을 적용하게 되면 image plane이 $z=1$인 위치가 아니라 틀어진 형태로 다른 곳에 존재하게 되는 것이다.