[시각지능] DLT

Computing with homographies

이번에는 direct linear transfomration(DLT)이라는 parameter estimation 방법에 대해서 알아보고자 한다. 2D homography estimation을 어떠한 식으로 할 수 있는지 알아보려는 것이다.
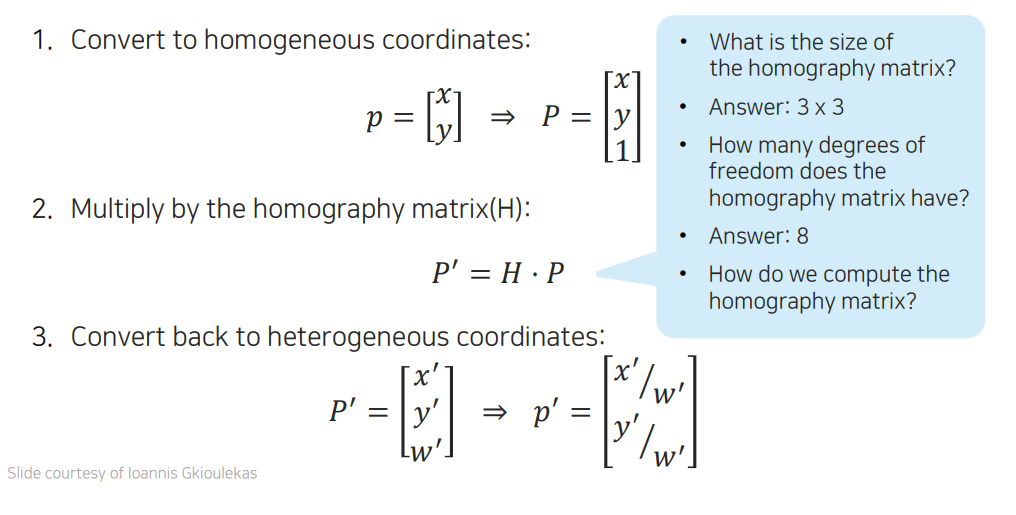이전까지는 2개의 대응점이 있다고 했을 때, 이들 사이에 존재하는 2D transformation 관계가 어떠한 식으로 modeling 되는지 $3\times3$ matrix를 통해서 알아보았다. 이번에는 이렇게 modeling 된 parameter를 구하는 방법에 대해서 알아볼 것이다.

가장 먼저 heterogeneous coordinate로부터 homogeneous coordinate로 변환을 시켜야 한다. 이는 간단하게 마지막에 1을 추가해주기만 하면 된다. 그리고 우리는 homography matrix를 $H$라고 부르고, 이를 homogeneous coordinate에 곱해줘서 다른 image에서 어디에 맺히는지를 추정할 수 있게 된다. 반대로 point 2개가 주어졌다고 한다면, 이 둘 사이의 관계인 $H$를 구할 수도 있는 것이다. 이를 homography estimation이라고 하는 것이다. 이렇게 구해진 $P'$이 주어진다고 한다면 맨 마지막에 존재하는 $w'$을 나눠주어 normalization을 해줌으로써 이를 다시 homogeneous coordinate에서 heterogeneous coordinate로 변환시킬 수 있다.

$H$를 $P'$과 $P$ 사이에서 구하고자 한다면 얼마만큼의 DOF가 있는지를 먼저 알아야 한다. 일반적인 homography matrix는 $3\times3$ matrix로 9개의 entry가 있는데, 9개의 entry 중에서 homogenenous coodrinate를 사용함으로써 scale invariance 특성을 가지게 되어 DOF는 8이 된다. 그렇다면 우리는 지금부터 DOF4가 8인 homograph matrix를 estimation하는 방법에 대해서 알아 볼 것이다.

The direct linear transformation(DLT)

Homography estimation을 하는 대표적인 알고리즘이 바로 DLT이다. DLT는 그저 linear하게 regression하는 방법으로 data가 주어졌을 때 parameter를 찾을 수 있다.

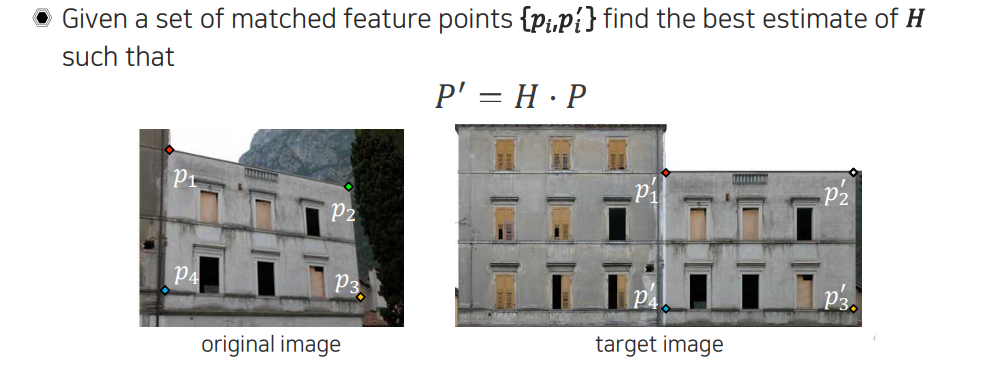DLT를 하기 위해서 가장 먼저 구해야하는 것이 바로 $H$이다. $H$를 알기 위해서는 또한 $P$와 $P'$을 알아야 $H$를 파악할 수가 있다. $P$와 $P'$ 사이를 구하는 것은 correspondence를 구하는 것과 같다. 그래서 먼저 key point detection, description, matching을 통해서 대응점들을 미리 구해놔야 한다. 위와 같이 4개의 point들이 matching이 된다고 생각해보자. 이때, original image와 target image 사이의 관계가 $H$로 modeling이 될 것이고, $H$ model의 parameter들이 어떻게 결정이 되는지를 우리가 구하고 싶은 것이다. 사실 위의 관계식은 linear하게 볼 수 있기 때문에 식이 특정 개수 존재하게 되면 $H$를 구할 수가 있게 된다. 그렇다면 몇개의 대응점이 존재해야 $H$를 구할 수가 있을까?

Determining the homography matrix

먼저 $P'=HP$를 element-wise로 나타낼 수 있다. 여기서 $\alpha$는 scale-invarint하게 하기 위해서 적어준 것이다. Matrix form을 하나씩 연립 방정식 형태로 적을 수가 있다. 여기서 $\alpha$는 우리가 관심있는 대상이 아니기 때문에 전부 나누어서 제거를 할 것이다. 그리고 2개의 식을 하나로 합치는 식으로 해서 마지막과 같이 2개의 식으로 표현할 수 있게 된다.
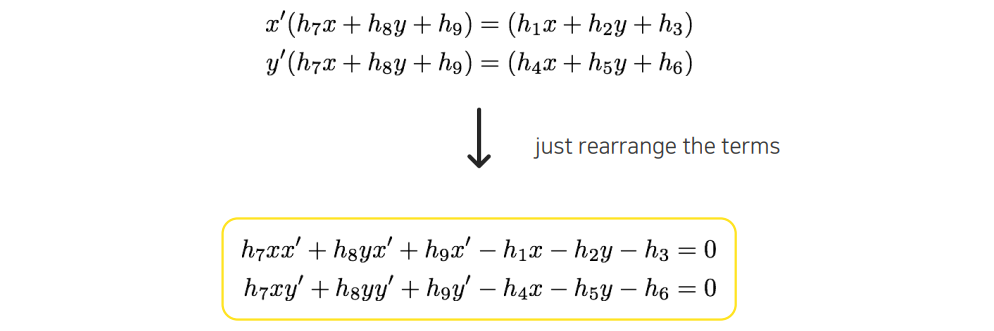그래서 2개의 point가 주어졌을 때 정리된 식을 보면 총 2개가 남게 되는 것을 알 수 있다. 이렇게 정리된 선형 방정식 2개를 우리가 관심있어 하는 $h$와 관련된 parameter로 정리를 하게 된다. 식 2개를 자세히 보면 해당 식에만 등장하는 parameter들이 3개씩 존재한다. 이렇게 정리가 된 선형 방정식을 보게 되면 이를 다시 matrix로 표현할 수 있게 된다.
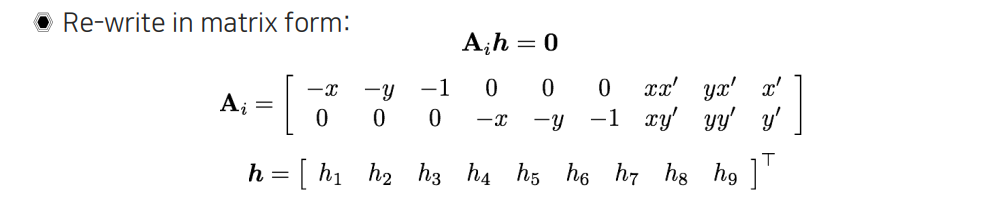이를 정리해서 matrix 형태로 위와 같이 $A_i$와 $h$로 표현할 수 있다. 따라서 $A_ih=0$이라는 식이 총 2개의 선형 방정식을 나타내게 된다. 하나의 correspondence를 통해서 얻을 수 있는 식은 2개가 된다. 우리가 찾고자 하는 $h$는 총 9개이고 scale invariance 특성으로 인하여 8개의 $h$만 구하면 되기 때문에 결과적으로 총 4개의 대응점만 존재하면 $H$를 찾을 수가 있는 것이다.

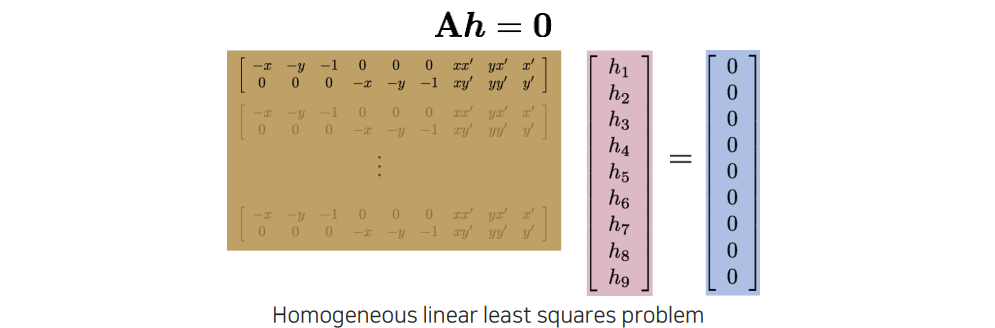총 4개의 correspondence를 이용해서 위와 같이 $Ah=0$인 식을 다시 만들 수가 있다. 사실 8개의 식보다 더 많은 식을 사용할 수도 있다. 사실 이 세상에는 noise들이 굉장히 많기 때문에 정확하게 0이 되는 값들을 찾기는 어려울 것이다. 그래서 우리는 이러한 문제를 homogeneous linear least squares problem으로 바꿔서 풀어야 한다. 결국 우리는 SVD를 이용해서 문제를 해결해야 한다.

Singular value decomposition(SVD)

항상 어떠한 형태로 matrix가 존재하든 상관없이 SVD는 존재하게 되어있다. 그래서 SVD를 하게 되면 orthonormal matrix 2개와 diagoanl matrix 1개로 나눌 수가 있다. 여기서 diagonal matrix의 entry는 sigular value에 해당하게 된다.
SVD를 이용하게 되면 일반적인 total least squares problem을 풀 때 가장 쉽고 흔한 solver로 사용이 된다. Total least square의 경우 $Ah$의 L2-norm을 최소로 만드는 $h$를 찾고자 한다. 하지만 여기서 $h$가 항상 0이 되면 자명해지기 때문에 원하는 결과를 얻기 위해서 $h$는 0이 아닌 의미있는 해가 되기 위해서 $h$의 L2-norm이 1이 되는 일종의 constraint를 주게 된다. 이 해를 구해보면 가장 작은 eigenvalue를 취하는 eigenvector가 될 것이다. $A^TA$를 해서 eigenvalue를 구하는 과정은 결국 SVD와 동일하게 되어 마지막에 해당하는 $V$에서 가장 작은 singular value에 해당하는 singular vector를 찾으면 solution이 될 것이다. Singular value가 가장 작은 것에 대응되는 singular vector의 경우 가장 null vector에 근접하기 때문에 minimization problem을 풀 수 있는 것이다.

Solving for $H$ using DLT

$x$와 $x'$에 대한 관계들이 주어졌을 때, 우리는 하나의 correspondence로부터 $2\times9$ matrix $A_i$를 얻을 수 있고, 이를 최소 4 이상의 $n$개의 correspondence에 대해서 식을 재정의하여 새로운 system equation $A$를 만들 수 있다. 이로부터 SVD를 이용해서 $A$를 분해하고 가장 작은 singular value에 해당하는 singular vecotr $v$를 $h$의 solution으로 취할 수 있다. $h$의 차원이 9이기 때문에 이를 다시 $3\times3$으로 reshape하여 homography estimation을 할 수 있다.

DLT의 경우 linear한 model에 대해서만 성립한다. 즉, $Ax=0$과 같이 간단한 linear system을 세울 수 있어야만 한다. 그렇다면 non-linear한 경우에는 어떻게 해야할까? 이러한 경우에는 최대한 linear 형태로 approximation 등을 통해서 문제를 간단하게 만들어서 최대한 DLT로 initial solution을 구해야 한다. 여기서부터 반복적으로 최적화 과정을 통해서 objective function을 만들어 놓고 원래의 non-linear한 형태의 model을 만족하는 solution을 찾도록 해야한다. 그래서 DLT 하나만으로 최종 solver가 될 수도 있지만, 일반적인 문제에서는 최대한 linear하게 만들어 놓고 initial point를 구하는데 사용될 수도 있다. 또한 DLT의 경우 Gaussian noise와 같이 작은 noise는 다룰 수 있지만 일반적으로 outlier를 다루기는 어렵다.

Create point correspondence

우리는 이제 point들로부터 $H$를 구할 수 있게 되었다. 이때, point correspondence는 손으로 찍어도 되고 automation을 통해서 구할 수도 있다. Key point detection, description, matching 등으로 구할 수도 있는 것이다. 여기서 descriptor가 완벽하면 문제 없지만, 완벽하지 않은 경우에 automatic하게 찾을 경우에 잘못된 correspondence를 구할 수도 있다. 이러한 것을 outlier matching이라고 하는데, DLT를 사용할 때 outlier를 어떻게 다뤄야하는지도 주의할 필요가 있다. 다음에는 outlier를 어떻게 다루면서 matching을 할 수 있는지 알아볼 것이다.