[시각지능] RANSAC

Random Sample Consensus (RANSAC)

Linear least square estimation은 linear한 경우밖에 다루지 못하지만 그래도 굉장히 중요한 initial point나 대략적인 solution을 제공할 수는 있다. 이러한 방법은 outlier를 처리하지 못하는 단점이 존재한다. Outlier가 하나라도 포함이 된다면 linear solution에 문제가 생기게 된다.

이러한 matching problem에서 homography estimation을 할 때 어떻게하면 잘못된 matching을 버리고 좋은 matching들만 남길 수 있는지에 대한 algorithm으로 RANSAC에 대해서 알아보고자 한다.

RANSAC은 주변에서 자주 사용되는 실용적인 algorithm 중 하나이다. 영상 데이터나 parameter estimation과 관련된 분야에서 outlier나 noise에 robust한 algorithm을 만들어야 하는 경우에 대해서 많이 사용된다.

RANSAC에 대해서 알아보기 위해서 먼저 간단한 line fitting 문제를 살펴보고자 한다. 위와 같이 outlier들이 포함된 data point들이 있을 때, 위의 data를 가장 잘 표현하는 좋은 line을 찾고자 한다. Outlier들로 인하여 우리가 생각한 것처럼 실제로 좋은 line을 구하는 것은 불가능할 것이다. Outlier로 인하여 line을 구한다고 했을 때 bias가 존재하는 solution을 구하게 될 것이다.

RANSAC algorithm을 보면 best model을 찾을 때까지 동일한 과정을 반복하게 된다. 가장 먼저 무작위로 point들을 선택하게 된다. 이때 model을 fitting하기 위해서 최소한의 개수를 선택하게 된다. 여기서는 line이기 때문에 최소한 2개의 point가 선택되어야 한다.

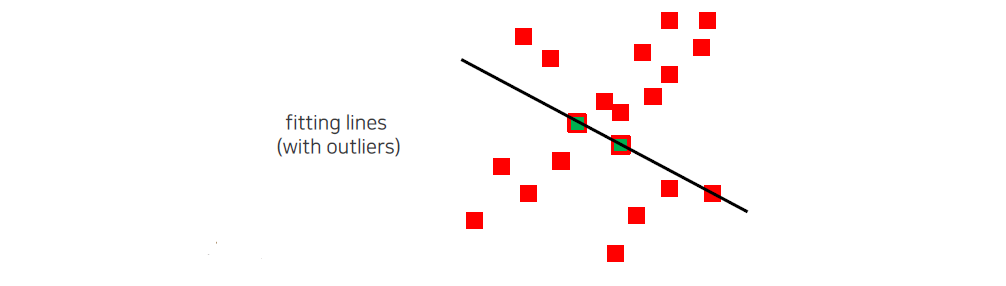다음은 이렇게 구한 point들로 model parameter를 구하는 것이다. RANSAC은 계속해서 동일한 과정을 반복하기 때문에 간단한 solver를 사용할수록 좋다.

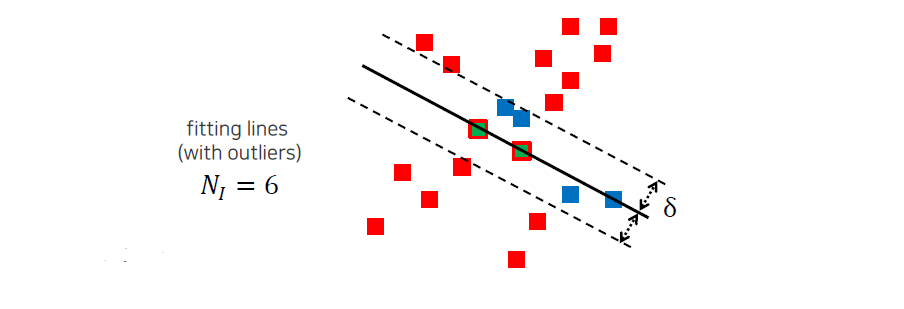다음에는 이렇게 구한 line이 얼마나 좋은지 평가를 할 것이다. $\delta$라는 threshold bound를 주었을 때 이 경계를 기준으로 안에 있는 point들 inlier라 하고 밖에 있는 point들을 outlier라고 할 것이다. 여기서 $\delta$는 사용자가 직접 정하는 것이고, inlier의 개수를 셀 것이다. 위에서는 6개가 inlier가 되기 때문에 이를 score로서 사용하게 될 것이다.

다시 이 과정들을 수행하게 되고, 이때 새롭게 얻은 inlier의 개수가 이전보다 많으면 이를 다시 score로서 사용하게 된다. Inlier가 많다는 것은 현재 model이 더 data에 어울린다는 것을 의미하게 된다. 무작위로 선택된 2개의 point로부터 RANSAC이 시작되기 때문에 어떻게 보면 운이 필요한 algorithm이 된다.

How to choose parameters

RANSAC은 항상 좋은 solution을 얻는다고 보장하지 못한다. RANSAC은 random algorithm이기 때문에 확률이 작용하기 때문이다. RANSAC을 얼마만큼 반복하는 것이 좋은지 판단하고자 할 때 우선 확률 $p$와 outlier ratio $e$를 가정하고, 여기에 model을 fitting하기 위해서 얼마나 많은 point들이 필요한지 $s$까지 가정할 것이다. 그리고 구해진 model이 얼마나 좋은지 판단하기 위한 threshold $\delta$까지 정해야 한다. 이러한 parameter들이 어떻게 정해지느냐에 따라서 우리가 반복 횟수 $N$가 어느정도여야 하는지 정해질 것이다. $N$만큼 RANSAC을 했을 때 inlier가 충분히 정해져 best model을 선택할 수 있다는 것이다. 하지만 실제로 이는 항상 보장되는 내용은 아니다. 이러한 관계성은 어느정도 보장이 되는 것이지 확신을 주는 것은 아니다.

RANSAC step by step

지금까지 line fitting에 대해서 RANSAC을 알아보았는데, 이번에는 homography estimation에서 matching에 outlier가 생겼을 때 어떻게 처리하는지에 대해서 살펴보고자 한다. 먼저 SIFT를 통해서 matching을 찾았다고 해보자.

그러면 위와 같이 outlier로부터 만들어진 correspondence와 inlier로부터 만들어진 correspondence들이 함께 존재할 것이다.

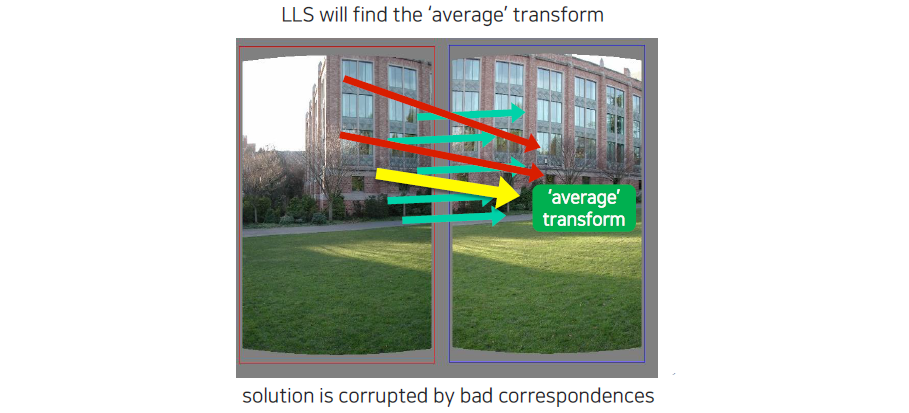처음에는 linear least square를 사용해서 average transform을 찾아야 한다. Outlier로 인해서 아래로 화살표가 가는 것을 볼 수 있다. 이는 outlier의 영향이 더 크다고 판단할 수 있는 것이다.

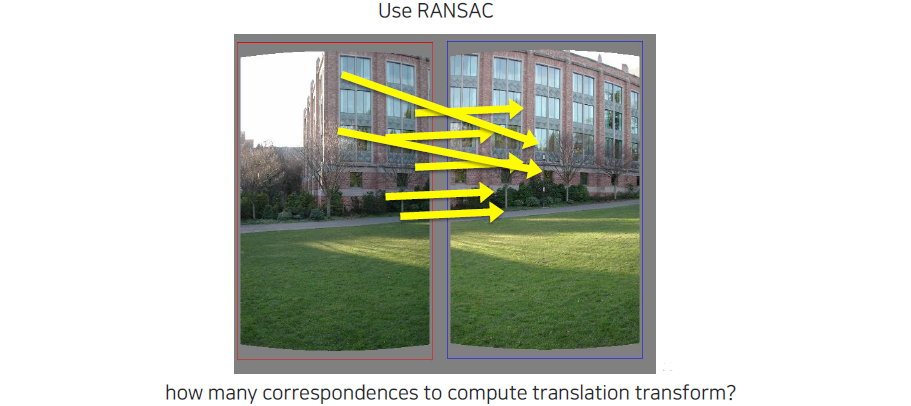우리는 translation을 구하기 때문에 하나의 correspondence만 있어도 motion vector를 구할 수 있다. 그래서 RANSAC model을 sampling할 때 필요한 correspondence sample 개수는 하나이다. 우리는 무작위로 하나의 pair씩만 sampling하면 된다.

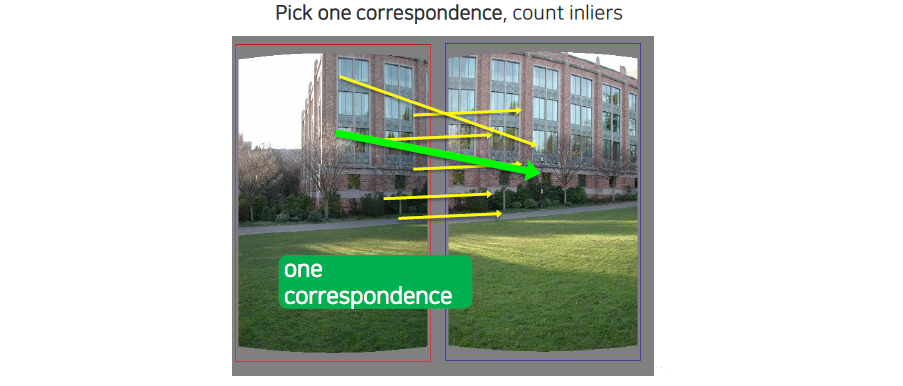하나를 sampling하게 되면 correspondence가 나오게 되고 이에 따른 inlier를 셀 수가 있다.

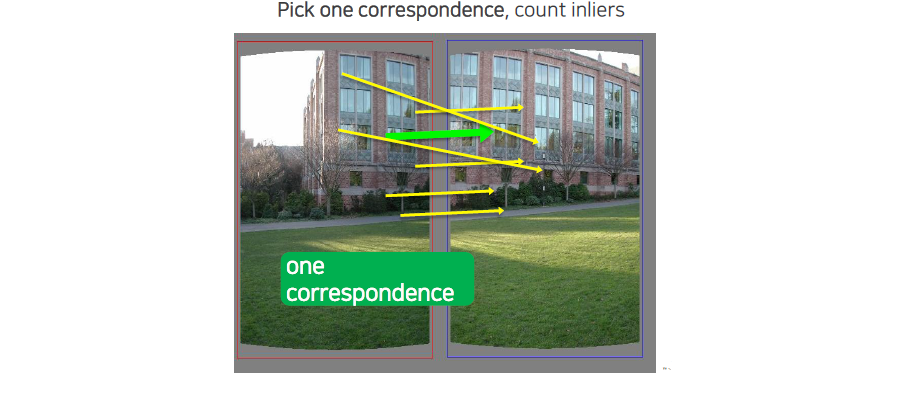우리가 어느 것을 선택하는지에 따라서 inlier의 개수가 달라지게 된다.

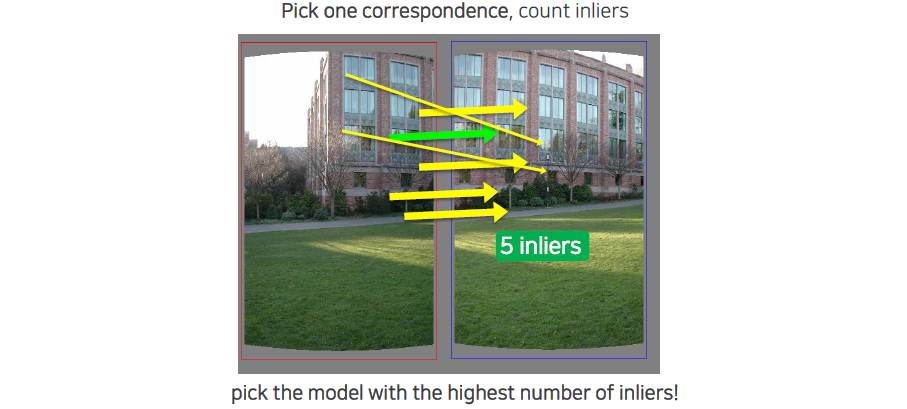우리는 sampling을 할 때마다 inlier의 개수를 세서 가장 많은 inlier가 생기는 것을 최종적으로 선택하게 될 것이다. 선택되 model에 의해서 outlier들을 제외시킬 수가 있고, 이로 인하여 robust한 parameter estimation이 가능해지게 된다.

Estimating homography using RANSAC

Homography를 구할 때 RANSAC은 위와 같은 순서로 진행이 된다. 먼저 4개의 point correspondence를 무작위로 선택을 한다. 우리가 구해야 하는 homography $H$는 DoF가 8이기 때문에 DLT를 하기 위해서 총 4개의 point correspondence가 필요한 것이다. 그 다음에는 $H$에 대해서 inlier가 되는지를 판단해야 한다. Inlier는 구해진 $H$를 point $P$에 transform 시켜서 생긴 point $\hat{P'}$와 처음에 미리 matching 시켜놓은 point $P'$ 사이의 distance가 어떠한 threshold보다 작은지를 판단해서 inlier의 개수를 세면 된다. 그래서 우리는 구해진 $H$에 대해서 inlier의 개수를 세서 inlier의 개수를 이전과 계속 비교해서 가장 많은 inlier를 가지는 $H$를 선택하면 된다. 최종적으로 모인 inlier들을 이용해서 $H$를 DLT를 통해서 다시 보정해주면 된다.

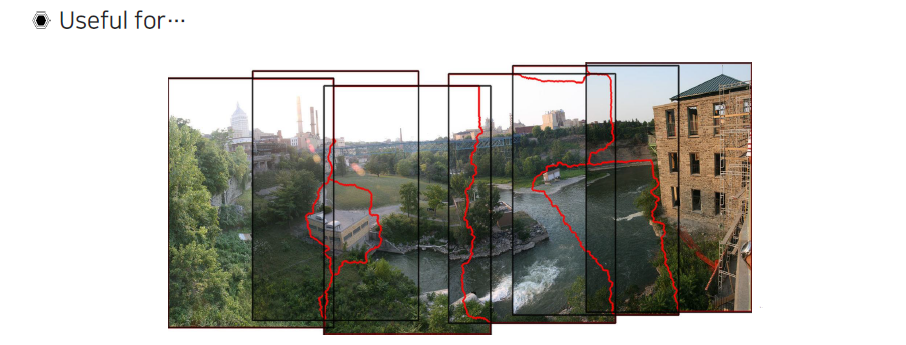이러한 RANSAC은 panorama estimation이나 3D reconstruction에서 굉장히 중요한 algorithm이고 여러 parameter estimation에서 많이 사용되는 방법 중 하나이다. 이는 굉장히 실용적이고 속도도 빠른편에 해당한다.

The image correspondence pipeline

Image의 대응점을 찾는 pipeline을 보면 중요한 point를 찾는 feature point detection 후에 이를 잘 설명하는 feature point description이 존재해야 하고, descriptor끼리 유사도를 비교해서 만든 matching으로부터 존재하는 outlier들을 filtering하는 RANSAC algorithm까지 필요하다. 이러한 과정을 통해서 panorama estimation이나 3D reconstruction 등 다양한 것을 할 수 있게 된다.