[시각지능] Triangulation

Two-view geometry

이번에는 카메라에서 3D pose를 추정하는 삼각측량법(Triangulation)에 대해서 알아보고자 한다. Triangulation은 image 2개가 있을 때 한 point가 서로 correspondence 관계에 있다고 하면은 카메라 좌표로부터 ray가 있다고 가정할 것이다. 이때 2개의 직선이 가지는 교점을 찾고자 하는 것이 triangulation이다. 이러한 원리로 여러개의 image가 주어졌을 때 3D reconstruction을 할 수 있는 것이다.

Triangulation

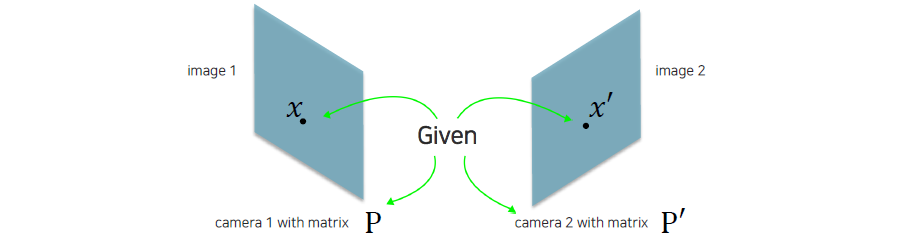Traingulation 문제에서는 먼저 2D point가 각각 주어지고 이 두 점은 각각 대응점이 된다는 가정이 존재한다. 어떠한 3D 좌표에 하나의 point가 있는데 이 point가 $x$와 $x'$에 projection 되는 것이다. 그리고 이 image 2개가 이미 calibration이 되어 있어서 camera pose가 미리 주어지게 된다. 추가적인 가정은 카메라 2개가 어느정도 거리를 유지하며 서로 overlap이 되어 있어야 한다. 그렇다면 이러한 point들을 이용해서 어떠한 3D point하고 mapping이 되는지 한번 알아보도록 할 것이다.

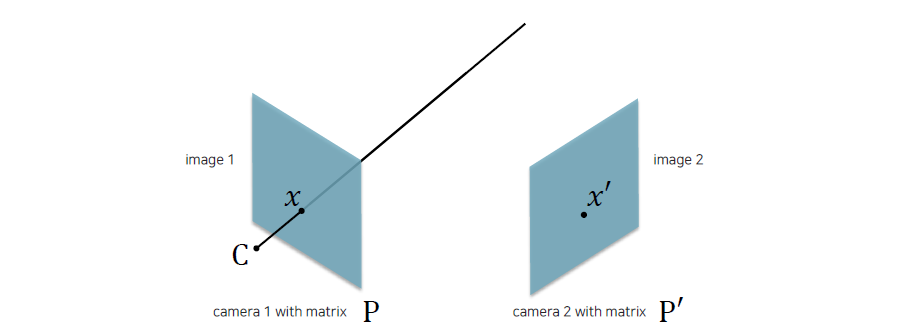카메라 center $C$가 주어진 상태에서 image plane의 한 점까지 선을 그리면 하나의 벡터가 만들어지게 된다. 그러면 이러한 벡터의 연장선 어딘가에 3D point가 존재한다고 할 수 있다.

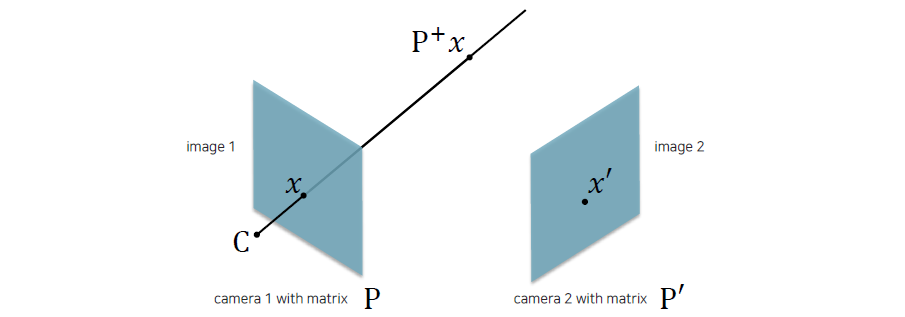우리는 이렇게 하나의 3D point를 위와 같이 수학적으로 표현할 수 있다. 우리는 카메라 center $C$를 $P$를 이용해서 $C=-R^Tt$로 구할 수가 있다. 이렇게 카메라 center를 먼저 구하고 $P$의 pseudo-inverse $P^+$를 구하고 이를 $x$에다가 곱하면 이 벡터의 방향이 나오게 될 것이다. 그래서 여기에다가 임의의 값을 곱해주게 되면 벡터 위의 한 점을 우리가 표현할 수 있게 된다. 직선 상의 모든 점들을 표현할 때 곱해주는 값만 바꿔주면 된다. 여기에 다시 앞에 $P$를 곱해주게 되면 원래의 $x$와 비슷한 방향이 나오게 될 것이다. 그래서 직선 위에 존재하는 point들이 $x$하고 mapping 되는 관계가 되는 것이다. 우리는 이를 backprojection이라 한다. Backprojection이라고 하는 것은 2D point $x$가 주어졌을 때 pseudo-inverse를 곱해줘서 2개의 point를 이어 방향을 구하는 과정이다.

그러면 이제 직선 상에 존재하는 모든 point들이 3D point가 될 수 있는 가능성이 있다. 이중에서 3D point를 결정해주기 위해서는 다른 observation이 추가적으로 필요하다. 그래서 두번째 image를 이용하여 어떠한 point가 진짜 3D point인지를 결정하게 된다.

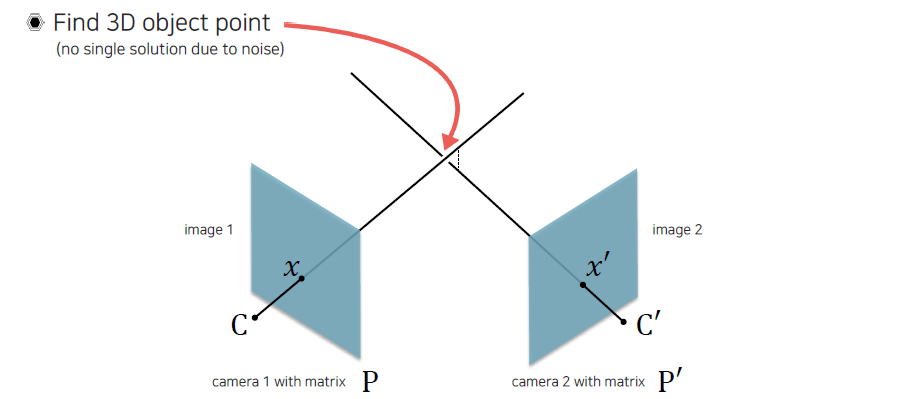두번째 image에서도 마찬가지로 ray를 이어주면 기존 ray와의 교점이 생기게 될 것이다. 우리는 이렇게 교점을 찾음으로써 3D point를 찾을 수가 있는데, 이때 2개의 line이 실제로 교차하는지를 판단해야 한다. 만약 noise가 없고 현실에서 이상적인 3D point가 카메라에 projection 되었다면 문제가 없을 것이다. 하지만 실제로는 많은 문제가 존재한다.

Harris corner detection나 SIFT 등의 algorithm에서 문제가 생기면 noise가 발생할 수 있다. 또는 camera pose estimatino을 할 때에도 nosie가 발생할 수 있다. 수학적으로 modeling을 했지만, 컴퓨터로 계산했을 때 어느정도 정확성에 한계가 존재한다. 이렇게 수치적인 한계로도 noise가 생기게 된다. 다양한 원인으로부터 교점이 정확하게 생기지 않을 수가 있다.

2개의 image에서 2D point $\{x_i, x_i'\}$가 뽑아지고 이 둘 사이의 관계가 정확하게 correspondence 관계로 존재한고 카메라 point가 주어져 camera matrix $P,P'$이 존재한다고 가정했을 때, 3D point $X$를 찾는 것이 바로 triangulation이다. 지금부터는 수학적으로 이 문제를 풀어보고자 한다.

우리는 현재 위와같은 식을 알고 있다. 3D point $X$가 있을 때 camera matrix $P$를 이용해서 2D point $x$를 projection하여 구했었다. 우리는 여기서 $x$와 $P$를 알고 있고 $X$는 unknown이 된다. 우리가 이 3D point를 구하고자 한다면 image 한장으로는 부족하다. 그래서 image 2장을 이용해서 연립방정식으로 문제를 풀고자 한다.

$x$는 homogeneous coordinate에서 관찰된 point이고, 이로 인하여 scale $\alpha$를 곱해도 불변성이 존재하게 된다. 우리는 이로부터 ray direction만 보고 위의 식을 정리하고자 한다. .

Linear algebra reminder: cross product

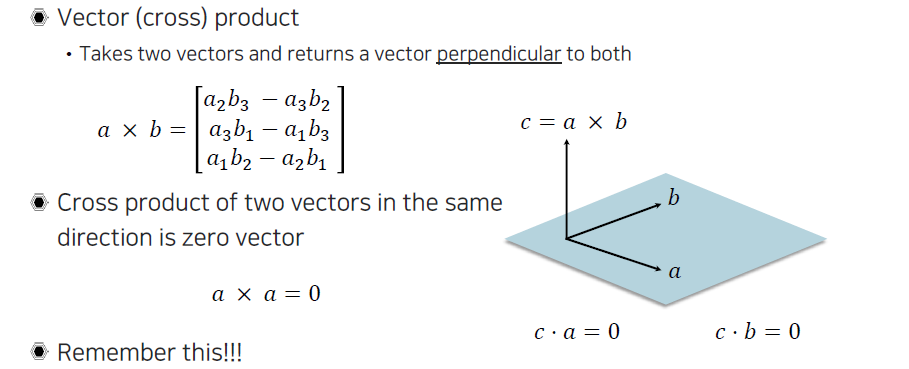이 식을 정리하고자 할 때 cross product를 사용하고자 한다. Cross product는 2개의 벡터가 있을 때 수직한 벡터를 구할 수가 있다. 이렇게 구한 수직 벡터는 기존의 벡터와 곱했을 때 직교하기 때문에 0이 나오게 된다. 또 다른 특성으로는 cross product를 자기 자신과 하게 되더라도 0이 나오게 된다.

Cross product는 또 다시 matrix multiplication 형태로 나타낼 수 있다. 그래서 cross product operation까지 포함한 것을 skew symmetric matrix라고 해서 새로운 matrix 형태로 표현할 수 있게 된다. 여기다가 벡터를 곱하게 되면 결과적으로 cross product를 한 것과 동일한 형태가 된다.

$x$와 $PX$는 방향이 동일하기 때문에 scale에 따라서도 방향이 같다. Cross product 특성상 같은 방향의 벡터를 연산해주게 되면 0이 나오게 된다. 그래서 $x$와 $PX$를 cross product 연산을 해주게 되면 0이 되는 것을 이용해서 선형 방정식을 만들 것이다.

위와 같이 식을 정리해서 cross product를 통해서 0꼴로 만들어준다. 하지만 이렇게 식을 정리하면 문제가 생긴다.

위의 2개의 식을 combination해주게 되면 마지막 식을 표현할 수가 있다. 그래서 이러한 관계면 linear dependency가 존재하게 되어 3개의 연립 방정식이지만 실제로는 2개의 선형 방정식만을 얻게된다. 결국 우리는 하나의 image에서 2D에서 3D point로의 correspondence로부터 최대 2개의 식을 얻게되는 것이다.

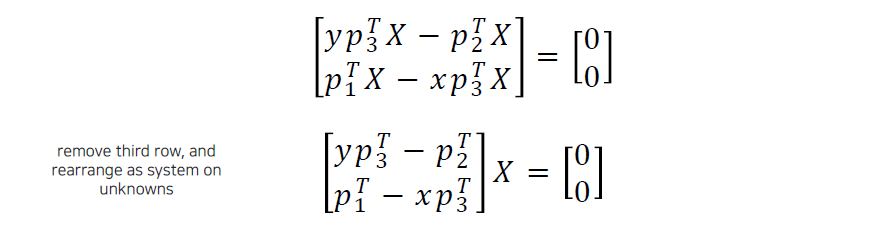그래서 우리는 2개의 식을 얻어올 수 있고 위와 같이 정리해서 $X$를 빼내올 수 있다. 이렇게 정리함으로써 unknown $X$에 대한 식으로 정리할 수 있게 된다. 여기서 문제는 $X$에는 총 3개의 unknown value가 존재한다. 그렇기 때문에 image가 하나 더 필요한 것이다.

최종적으로 카메라 2개에서부터 온 식을 통해서 선형방정식을 세워준다. 그러면 unknown이 3개고 식이 4개가 되어 overdetermined system이 된다. 결과적으로 $A_iX=0$이라는 식을 풀 수 있어 이를 풀어주기만 하면 된다. 우리는 이러한 식을 SVD를 이용해서 풀어주면 된다.

Image 2개로부터 3D point를 구하는 것은 사람의 관점으로 보았을 때 2개의 눈으로 구하는 것과 같다. 사람의 눈은 한쪽을 감았을 때 실제로 3D를 인지하지 못한다.