[시각지능] Semantic segmentation 1

What is semantic segmentation?

Semantic segmentation은 image의 각 픽셀마다 어떠한 category에 속하는지를 분류하는 인식 문제의 일종이라고 볼 수 있다. Image classification의 경우 image가 있으면 어떠한 category에 속하는지 하나의 class로 분류할 수 있다. Semantic segmentation은 각 픽셀마다 해당되는 category로 분류하는 좀 더 dense한 classification이다. Semantic segmentation의 경우 object를 각각 분류할 수 있지만 동일한 object가 몇개가 존재하든 상관없이 동일한 category로 분류하게 된다.

위의 예시를 보면 사람이나 자동차 등 각 object에 해당하는 픽셀들이 segmenation되는 결과를 볼 수 있다. 만약 자동차가 여러대 존재하여도 해당 픽셀이 자동차임을 알려주기만 할 뿐이지 각각의 자동차 개별로 인식하지는 않는다.

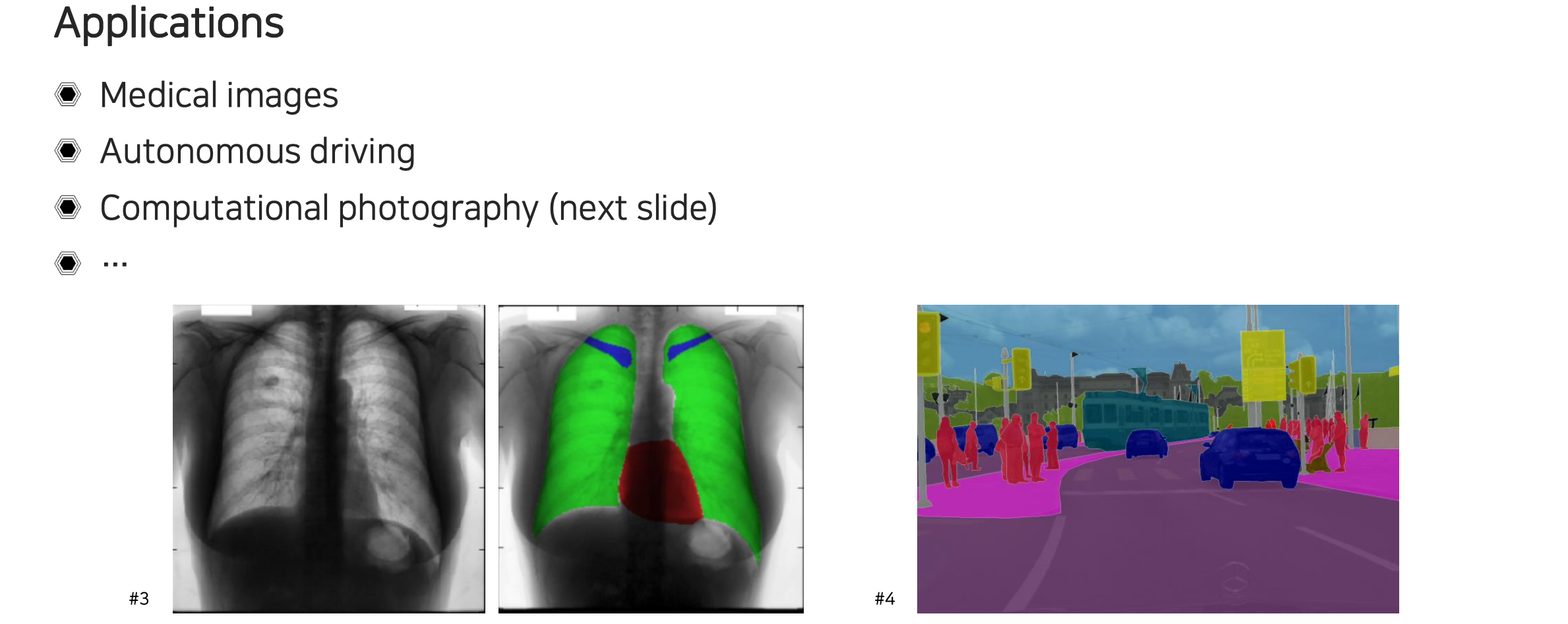Semantic segmentation에는 다양한 application들이 존재한다. 어떠한 scene을 이해하고 해석하는데 있어서 모든 application의 앞단에 사용이 가능할 것이다. 대표적으로 medical image에서 병변을 찾아내고 진단하는 경우가 있다. 또한 자율주행을 위한 핵심 기술로써 장면을 먼저 이해를 해야하는데, 이때 도로와 인도를 구분하고 주변의 사물들을 잘 파악하는데 사용이 된다. 어떠한 픽셀이 어디에 속하는지 정교하게 판단을 해야한다.

Fully Convolutional Network (FCN)

Semantic segmentation을 구현하는 대표적인 방법으로 fully convolutional network(FCN)이 있다. 굉장히 고전적인 방법일 수 있지만 이 연구가 semantic segmentation에 있어 획기적인 결과를 만들어냈다. FCN이 등장하기 전에는 semantic segmentation을 구현할 때 먼저 object proposal을 통해서 bounding box들을 prediction을 해야했다. 이러한 proposal들을 기반으로 box들 내에 어떠한 물체가 존재할 것이라는 가정과 함께 image classification을 수행했다. 이렇게 segmentation을 한다고 했을 때 가장 먼저 전경과 배경을 구분을 하고, 분리한 bounding box들 내에서 전경에 대해서 image classification을 수행했었다. 좀 더 자세하게 object proposal의 경우 over-segmenation을 해서 그 결과들을 계층적으로 비슷한 것들끼리 묶어준다. 이렇게 계속해서 비슷한 결과끼리 묶어가다보면 어떠한 물체라는 것이 파악이 될텐데, 이렇게 파악이 되면 bounding box를 이용해서 classification을 수행해서 어떠한 물체인지 파악하는 구조로 진행이 된다. 이렇게 다단계적으로 수행하게 되면 뒤쪽에서 분류를 한다고 했을 때 앞쪽에서 object proposal이 잘못되면 뒤에서도 문제가 발생할 것이다. 그래서 성능이 object가 proposal되는 상황에 bound되는 한계가 존재했다. 이러한 semantic segmentation approch를 픽셀 수준의 prediction으로 바꾸면서 end-to-end로 학습이 가능하게 된다면 performance bound를 우회할 수 있는 좋은 수단이 될 것이다.

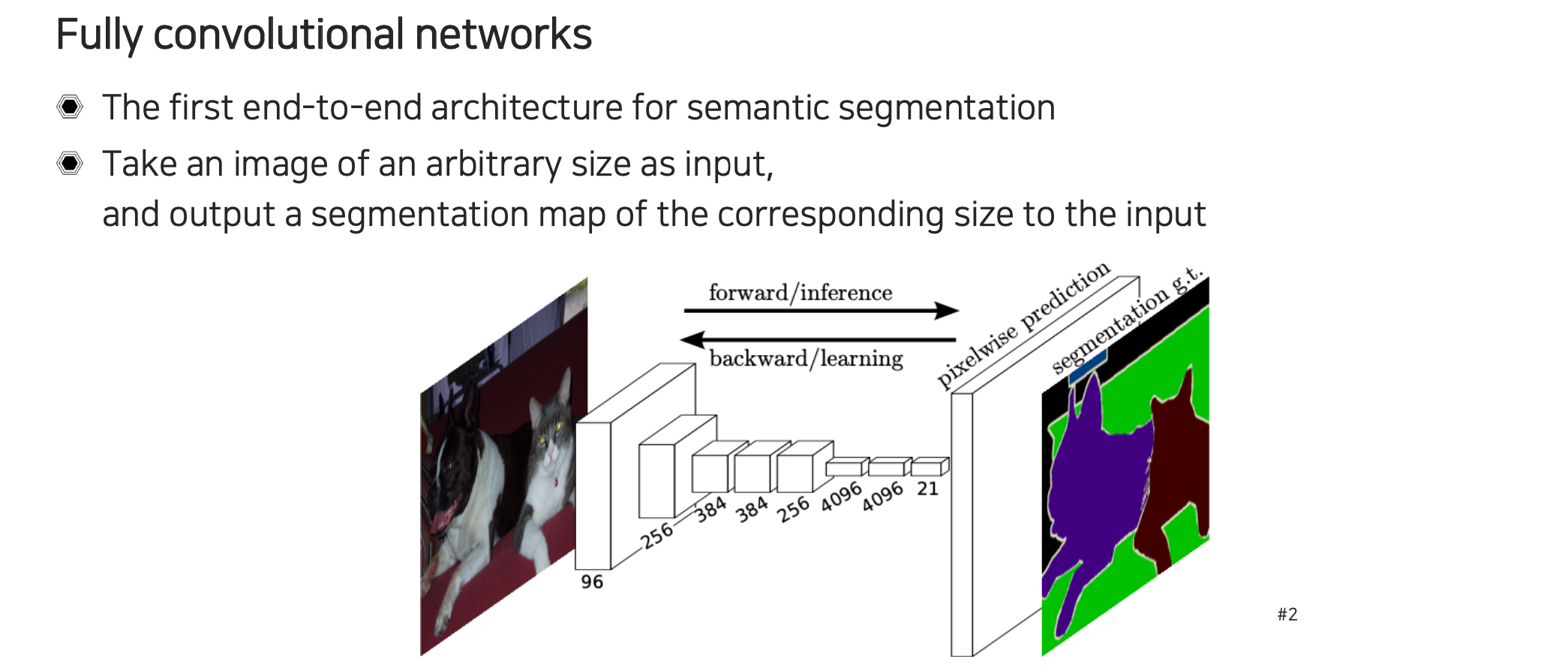그러한 방법을 제시한 것이 2015년에 제시된 FCN이다. FCN은 end-to-end architecture로 제시가 되었으며, semantic segmenation을 픽셀 수준으로 할 수 있는 간단하면서도 잘 디자인된 모델이다. Input으로는 이전처럼 고정된 크기가 아니라 임의의 크기의 image를 사용할 수 있게 되었고, output으로는 segmentation map이 나오게 된다. Output의 크기는 input과 동일하게 맞춰져서 나오게 된다. Segmentation network를 이용해서 prediction이 나오게 되면 정답지로 픽셀마다 존재하는 값들과 비교를 통해서 loss를 계산하고, 이를 통해서 back-propagation을 수행하는 식으로 학습이 된다. 이렇게 supervised learning의 형태로 input image와 ground truth pair가 존재할 때 이 사이의 차이로 학습이 진행되는 구조이다.

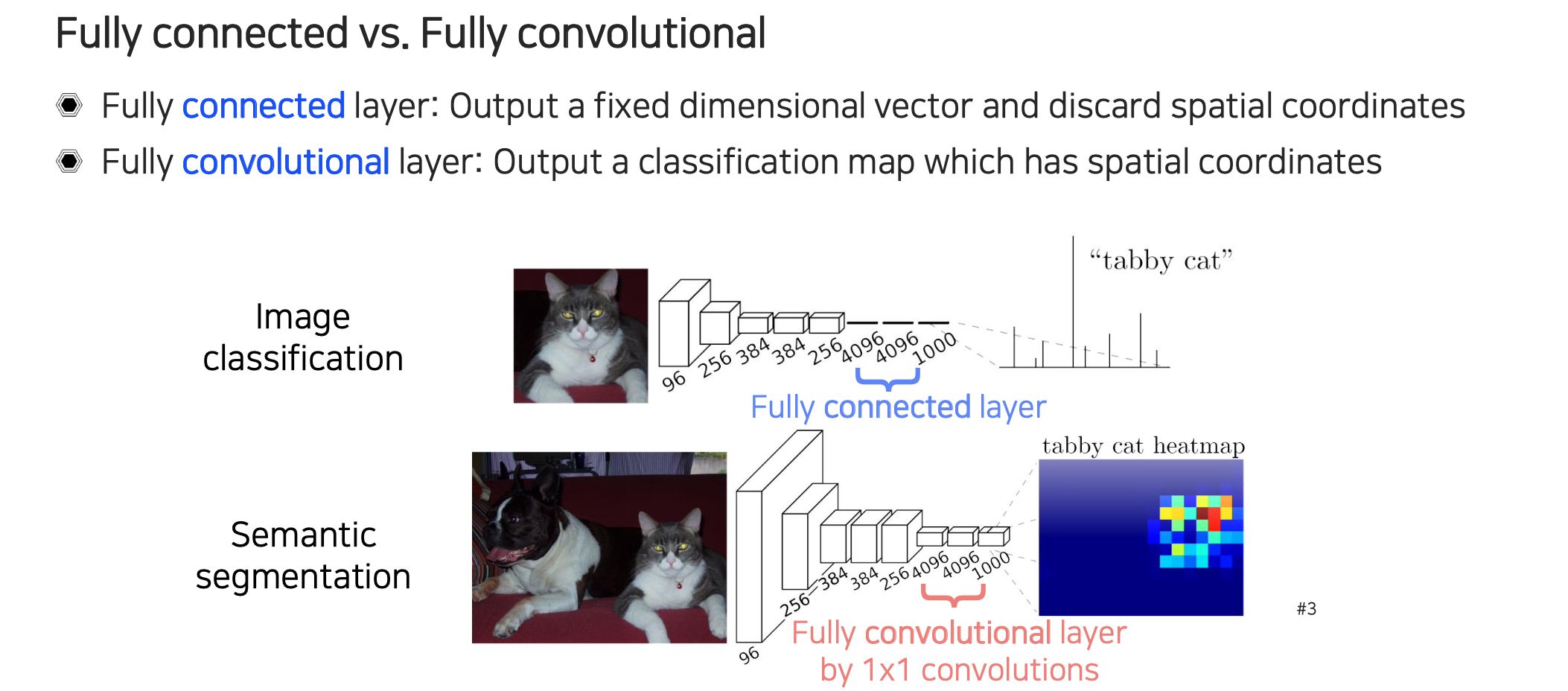여기서 잠시 fully "connected"와 fully "convolutional"이라는 용어가 헷갈릴 수가 있다. 먼저, fully connected layer의 경우 output이 고정된 차원의 vector가 나오게 된다. 그래서 image classification과 같이 마지막에 사용이 되는 것이 fully connected layer이다. 이번에 살펴보고 있는 fully convolutional layer는 이와는 조금 다르며, 여기서는 특히 $1\times1$ convolution을 수행하게 된다.

Fully connected layer의 경우 input으로 들어가게 되는 feature는 공간상의 정보를 포함하고 있게 된다. 영상의 aspect ratio에 맞춰서 spatial size가 어느정도 비율로 남아있게 되는데, 여기에 fully connected layer를 적용하게 되면 이러한 공간적인 정보를 전부 무시하게 된다. 그래서 output으로는 항상 고정된 크기의 결과가 나오게 된다.

Fully convolutional layer의 경우 이러한 제약이 없이 input의 크기에 맞춰서 output의 크기가 조정이 되는 유연한 구조를 가지고 있어서 spatial coordinate와 같은 정보들이 그대로 남아있게 된다.

기존의 image classification에서 fully connected layer를 이용해서 굉장히 좋은 성능을 보여주었는데, 이를 fully convolutional layer를 이용해서 똑같이 해석할 수만 있다면 그대로 좋은 성능을 가져올 수 있을 것이다. 그래서 여기서 fully connected layer를 $1\times1$ convolution으로 해석이 가능하다고 하면 어느정도 동치로 볼 수가 있다는 것이다. 그러면 이러한 동치로부터 fully connected layer로 성공했던 사례를 fully convolutional layer 형태로 구현했을 때에도 여전히 성능을 유지할 수 있게끔 구조를 만든 것으로 볼 수 있다.

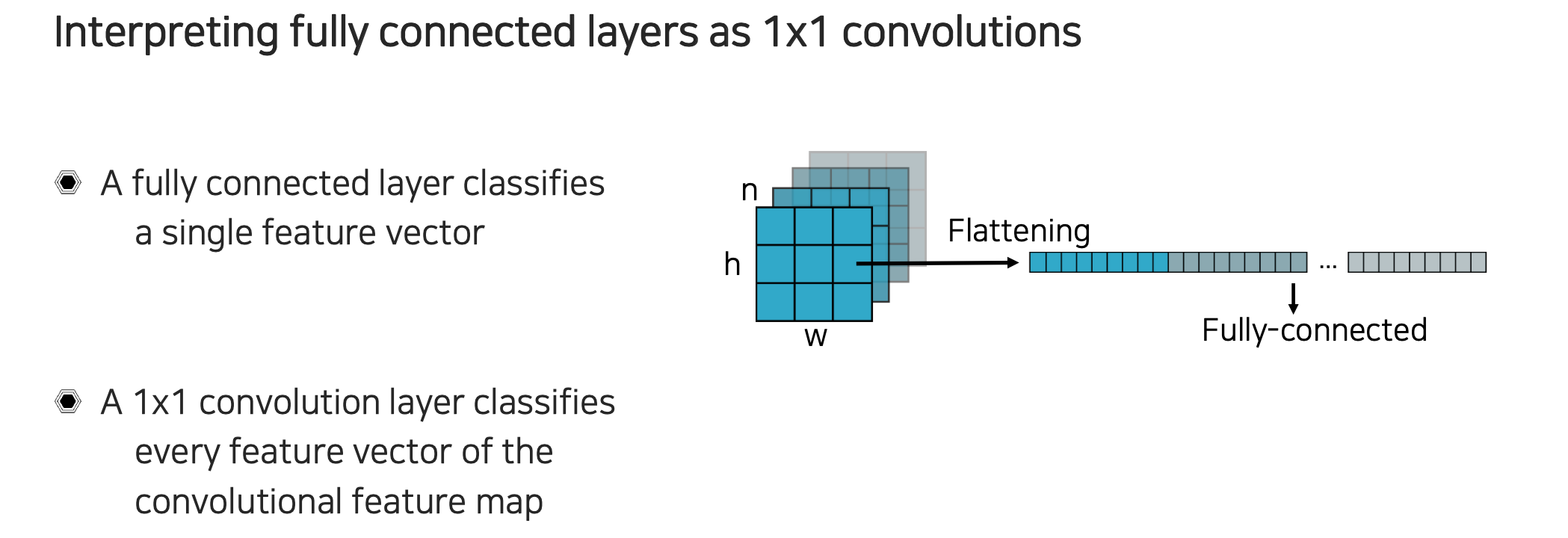
Fully connected layer는 공간축과 채널축을 가지는 feature가 들어왔을 때 단순히 flattening을 시키게 된다. 모든 차원의 크기를 곱하게 되는 vector를 만들고 쌓아서 최종적으로 고정된 크기의 결과를 만들어 낸다.

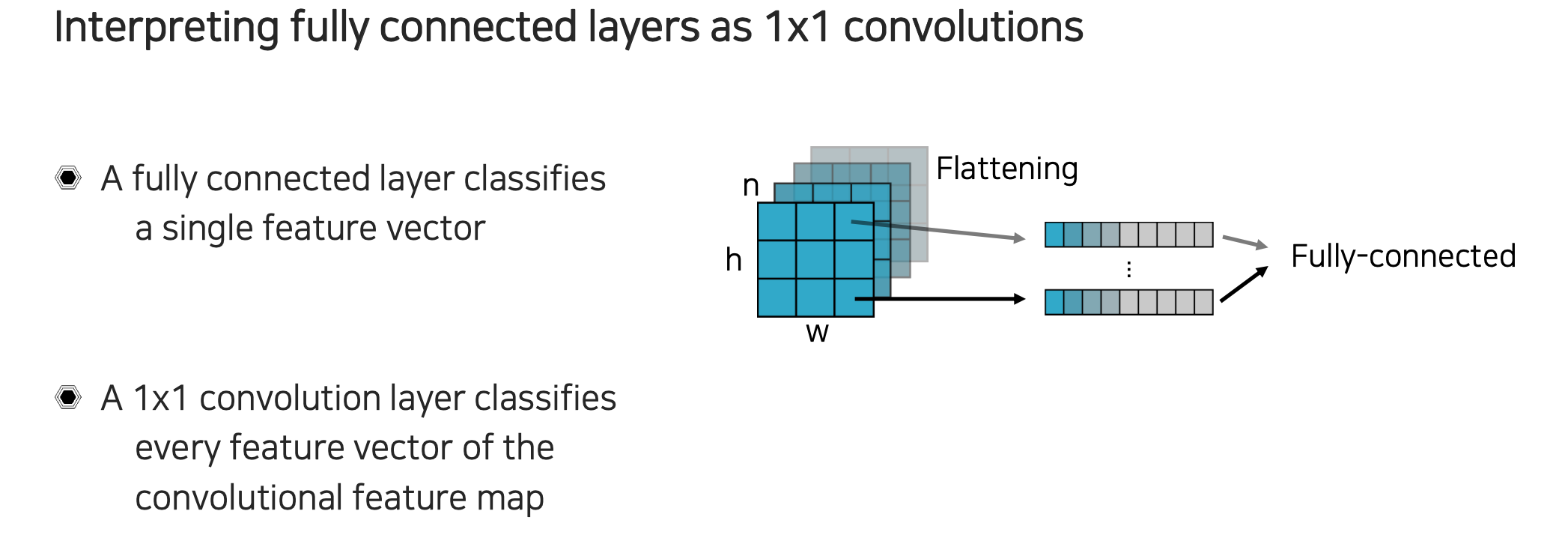이번에는 flattening을 할 때 $hwn$을 전부 하는 것이 아니라 각 픽셀 위치에 있는 채널축 값들만 가져온다고 생각해볼 수 있다. 그래서 각 위치마다 feature vector를 만든다고 생각할 수 있다. 그리고 이를 각각 독립적으로 fully connected layer에 넣어준다. 각각의 vector들이 있을 때 fully connected layer는 그냥 weight matrix 하나의 형태로 표현할 수 있게 된다. 단순히 matrix multiplication으로 볼 수 있다.

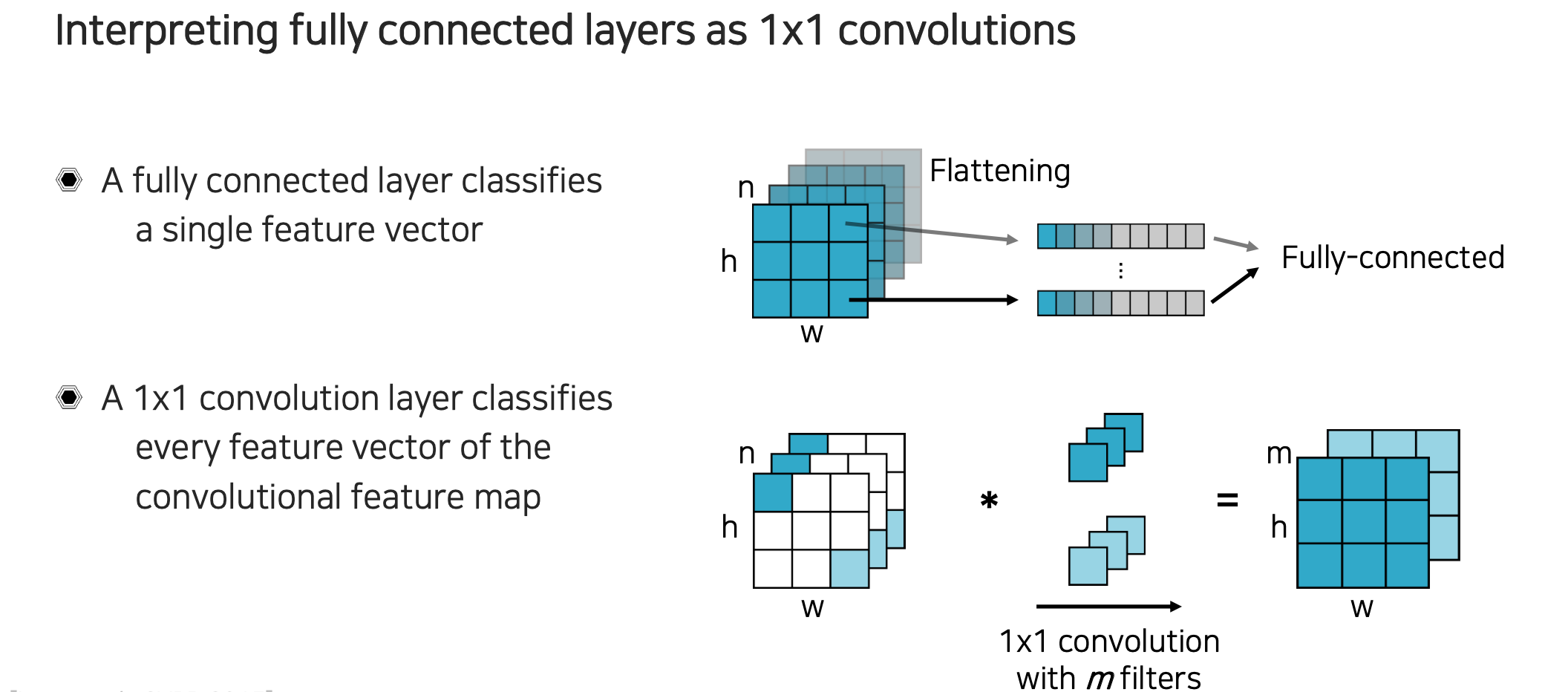위의 결과와 $1\times1$ convolution layer를 만들어서 각 feature vector의 위치를 convolution하는 것과 동치라는 이야기다. 각 픽셀에 해당하는 feature에 맞도록 $1\times1$ convolution을 대입하고 전체를 convolution을 해주면 위에서 weight matrix와 모든 feature vector의 matrix multiplication 하는 것과 동일하게 되는 것이다. 그래서 $1\times1$ convolution을 $m$개 사용한다는 것은 weight matrix에서 $m$개의 row vector를 사용한다는 것과 동일한 이야기다. Fully connected layer를 통해서 나온 feature vector들을 모두 쌓아서 모양을 잘 조절해주면 $1\times1$ convolution 결과와 같은 feature map 형태로 잘 만들 수가 있게 된다. Fully connected layer를 픽셀마다 독립적으로 본다고 하면 결국에는 $1\times1$ convolution으로 구현을 바꿔서 모양만 다른 결국에는 동일한 결과를 낼 수 있다는 것이다.

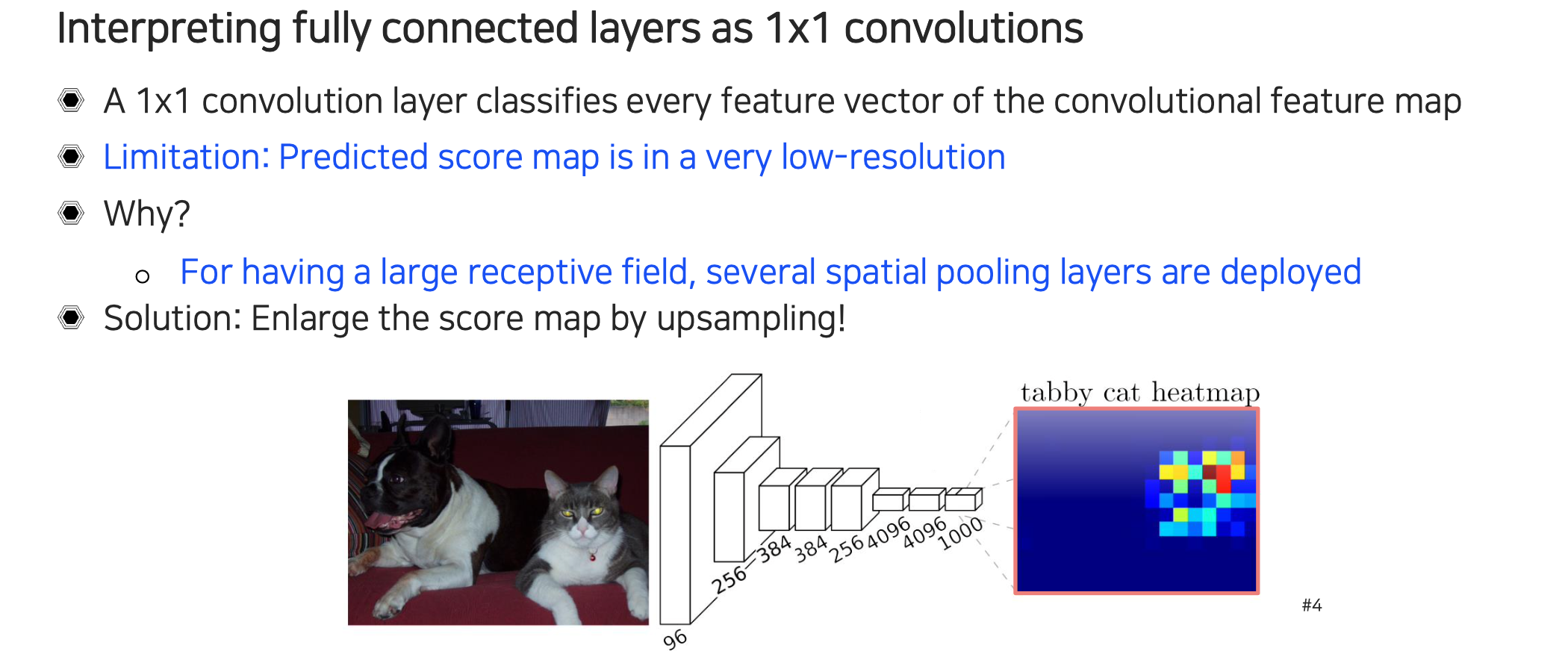그래서 image classification layer에서 마지막에 fully connected layer를 $1\times1$ convolution으로 바꿔서 모든 feature vector로부터 feature map을 만들어 각 위치마다 classification하는 문제로 바꾸어 준 것이다. 이렇게 했을 때 한계점은 마지막 fully connected layer를 $1\times1$ convolution을 적용한다 하더라도 여기에 적용되는 feature map이 이미 너무 low-resolution을 보인다는 것이다. 그렇게 되면 최종적으로 score map도 low-resolution을 보이게 될 것이다.

그렇다면 중간에 low-resolution이 되지 않도록 유지하면 어떠할까? 이러한 경우에는 우리가 receptive field를 크게 가져가지 못하는 문제가 생긴다. 마지막에 prediction 된 score 값은 어떠한 픽셀들을 보면서 왔는지에 따라 결정이 되게 되는데, 만약 중간에 pooling을 사용하지 않고 convolution만 잔뜩 쌓아서 만들게 된다면 아마 처음부터 좁은 부분만 보고 결과를 냈을 것이다. 너무 좁은 영역만 보고 값을 결정했기 때문에 신뢰도가 굉장히 떨어질 것이다. 해당 부분이 고양이인지 아닌지를 보기 위해서는 적어도 고양이 얼굴 크기 만큼의 영역은 참고해야 할 것이다. 그렇기 때문에 receptive field가 클수록 해당 영역이 어떠한 category인지 판단하기 쉬울 것이다. 사람들도 어떠한 픽셀을 볼 때 주변의 정보를 모두 보고 결정하게 된다. 이러한 것이 convolutional neural network에서도 마찬가지이기 때문에 중간중간 pooling layer를 통해서 효과적으로 receptive field를 확보해야 할 것이다.

그래서 이러한 spatial pooling을 사용하는 것이 resolution 측면에서는 굉장히 불리하게 되지만, accuracy 측면에서는 receptive field를 많이 가져가기 때문에 더 유리하게 되는 것이다. 그렇기 때문에 semantic segmentation에서 최종 score map은 image resolution과 비슷해야 하기 때문에 trade-off 관계를 가지게 되는 것이다. 이를 우회하기 위해서 사용하는 해결 방안으로 score map을 upsampling하는 방법이 있다. 최종단에서 upsampling만 하면 의미가 없고, 중간의 feature map을 upsampling해서 크게 만든 다음에 그 위에서 픽셀마다 classification을 해주는 것이다. 먼저 receptive field를 크게 만들고 작은 resolution의 feature map을 만든 다음에 다시 이것을 크게 키워서 각 픽셀마다 어디에 속하는지 주변 정보도 보면서 high-resolution으로 결정할 수 있도록 만드는 것이다.

Upsampling

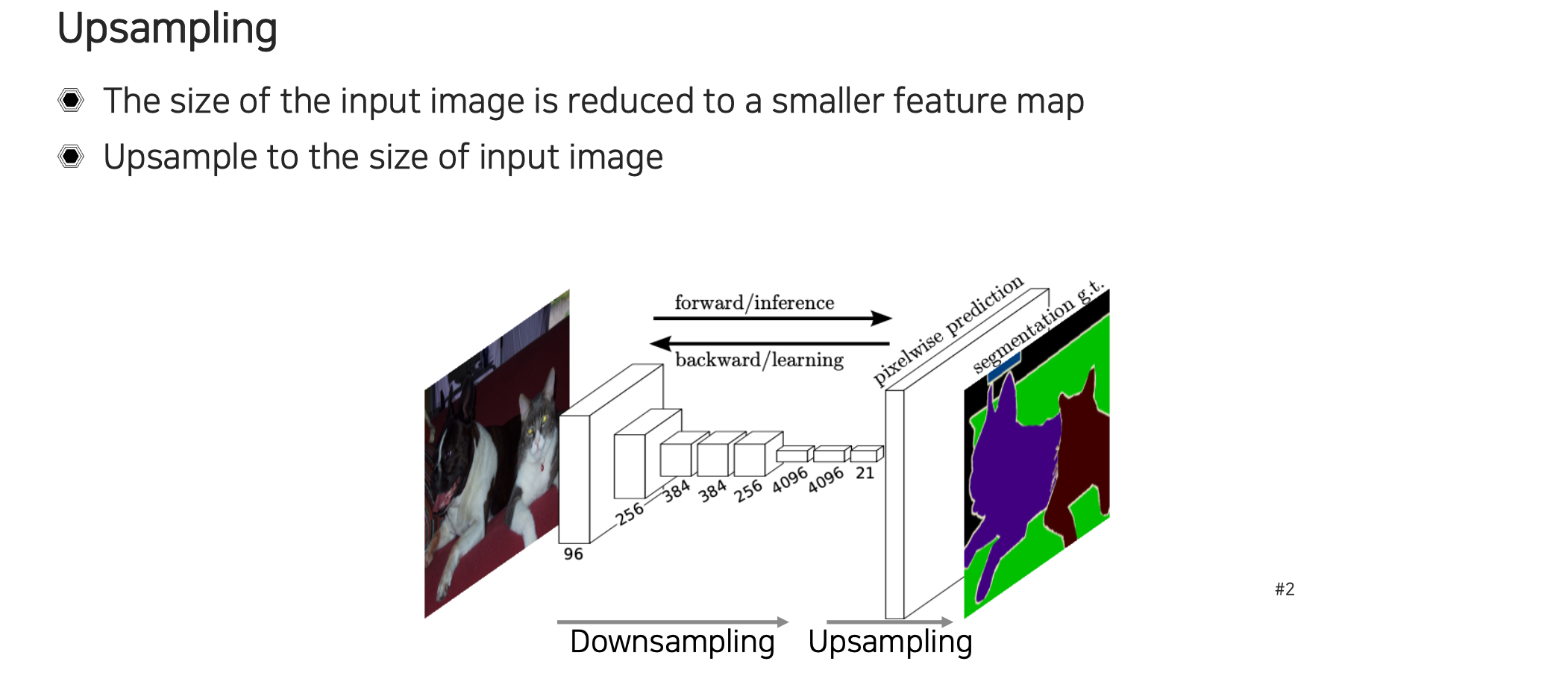지금부터는 어떠한 upsampling을 사용하는지 알아볼 것이다. 작은 feature map을 input의 크기만큼 키우는 것을 upsampling이라고 한다. Convolution을 계속 하면 feature map의 크기가 굉장히 작아지게 되는데 이를 원래 input의 크기로 만드는 upsampling 과정이 필요하다. 이러한 upsampling을 neural network에서 learnable하게 구현할 수 있는 방법이 여러 존재한다. 대표적인 unpooling부터 deconvolution이라고 불리는 transposed convolution 등이 존재한다.

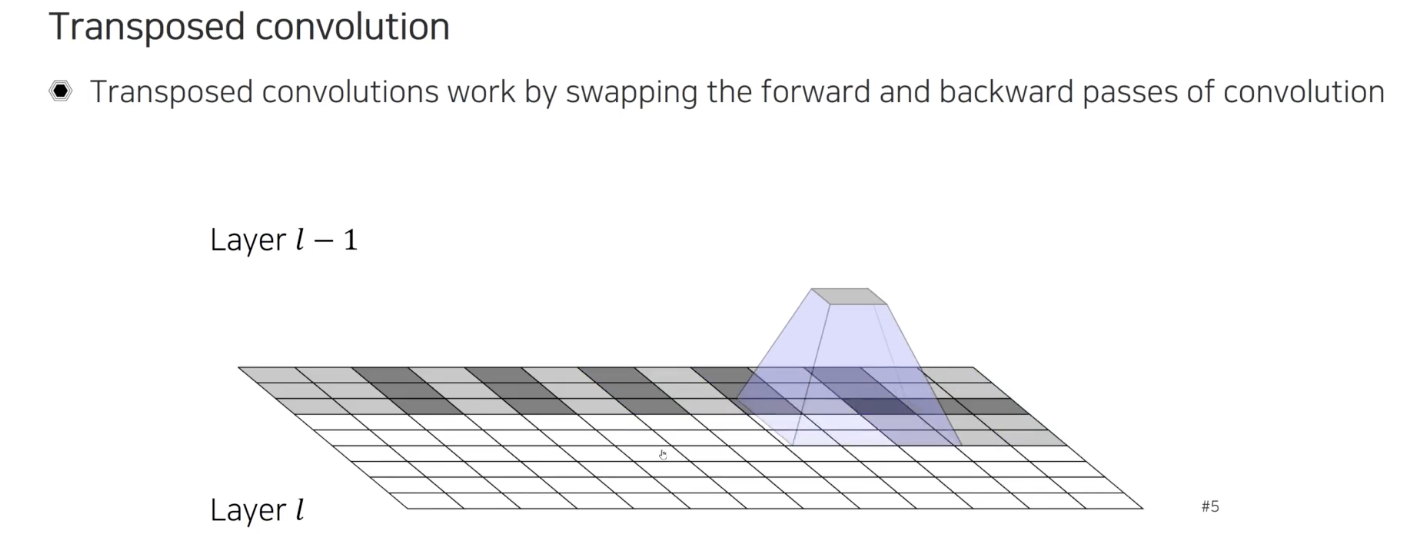먼저 transposed convolution에 대해서 알아보고자 한다. 일반적인 convolution은 여러 픽셀들을 보고 하나의 값을 결정하는 식으로 수행된다. Transposed convolution은 forward와 backward 과정을 바꿔준 것이다. 그래서 반대로 하나의 픽셀 값을 참조해서 큰 픽셀 값들을 채워넣는 식으로 수행된다. 위의 예시는 하나의 값에서부터 9개의 값들을 채워넣고 있다. 이렇게 더 많은 값들을 채워주다보니 다음 layer에서는 더 큰 결과를 얻어내는 upsampling이 수행되는 것이다.

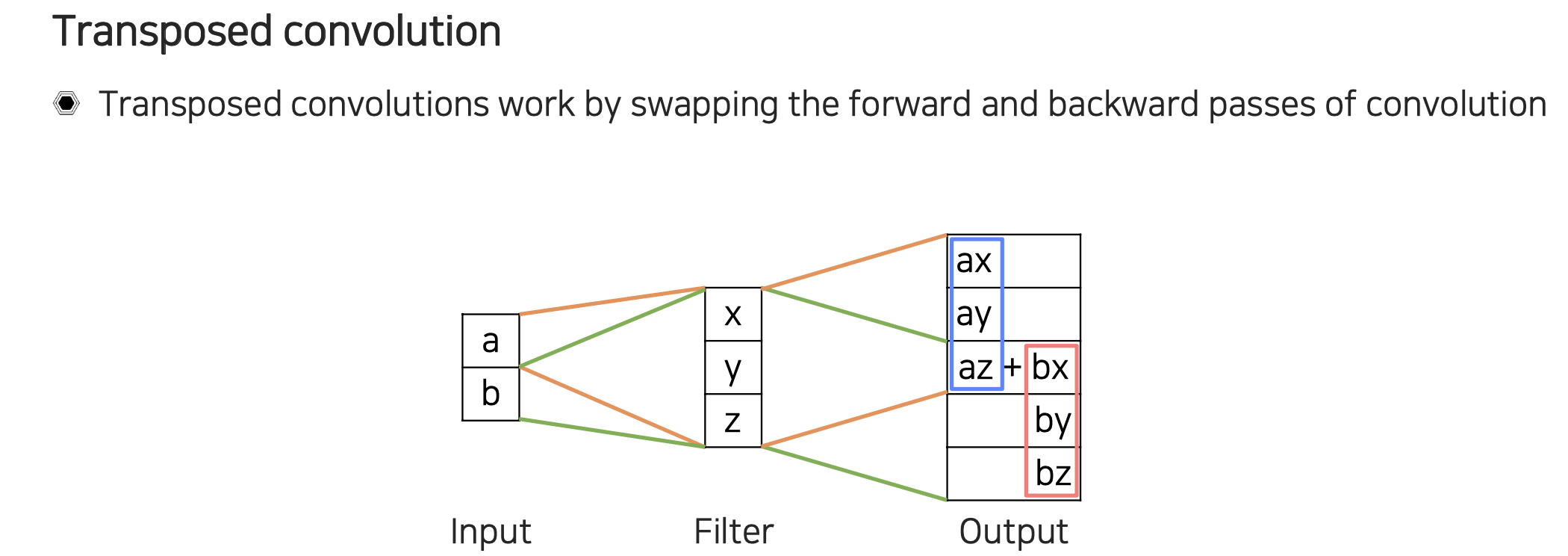이를 자세하게 살펴보면 $a$라는 값이 이전 layer에서 input feature map으로 주어졌다고 가정할 것이다. 이해하기 쉽게 filter가 1차원의 크기가 3이라고 한다면 이를 $a$만큼 scaling해서 3칸을 차지하게 된다. 바로 옆에 있는 $b$도 마찬가지로 scaling을 통해서 3칸을 차지할 수 있다. 이렇게 정보를 채워갈 때 stride만큼 이동하기 때문에 겹치는 부분이 생기고, 결과적으로 resolution이 이전보다 늘어나게 될 것이다. Transposed convolution은 겹치는 영역이 생겨 이들이 서로 중첩 되는 문제가 생기게 된다.

그렇기 때문에 transposed convolution을 수행하게 되면 checboard artifact가 생기게 된다. 이는 겹치는 영역이 균일하게 생기는 것이 아니라 특정한 step마다 생기게 된다.

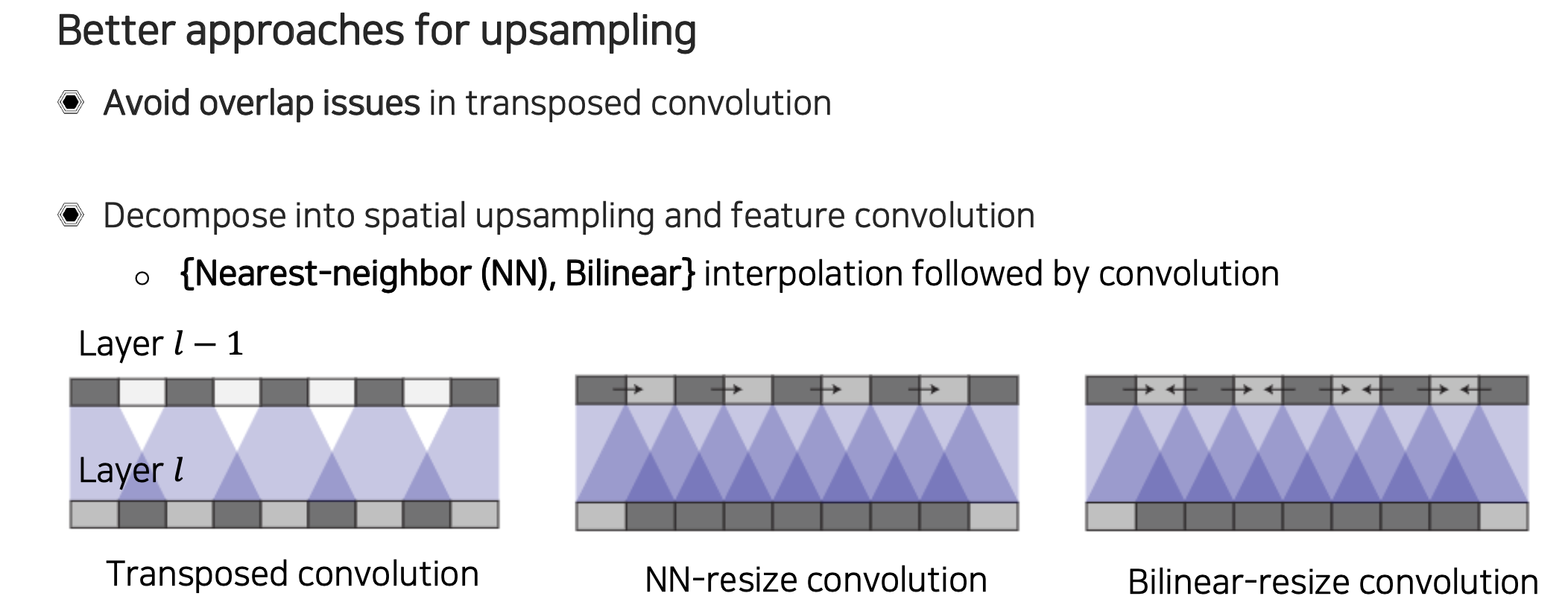이러한 transposed convolution이 학습과 성능에 방해가 되기 때문에 더 나은 방법들이 소개가 되었다. 그 방법으로는 spatial upsampling을 해주는 부분과 feature transformation을 해주는 부분을 분리하고 가는 것이다. Image를 interpolation하는 것처럼 feature를 먼저 공간축 상으로 upsampling을 해주고 그 다음에 convolution을 적용하는 것이다. 사실 transposed convolution을 사용해도 되고 안해도 되지만 여기서는 이해를 위해서 transposed convolution을 사용한다는 가정에서 어떻게 분리시키는지 알아보고자 한다.

만약 우리가 Nearest-neighbor(NN)을 먼저 적용해서 픽셀들을 옆 공간에 일부러 만들어서 채워 넣는다고 해보자. 그리고는 stride를 1씩 적용해보는 것이다. 이렇게 되면 transposed convolution을 적용한다고 하더라도 겹치는 부분의 개수가 일정해지게 된다. 이렇게 되면 checkboard artifact를 줄일 수 있게 된다. 비슷한 방식으로 Bilinear 방식으로 양쪽으로부터 값들을 채워넣고 transposed convolution을 적용할 수도 있다. 그런데 이렇게 값을 일정하게 채운다고 하더라도 중첩이 필요 이상으로 되어 값이 커지게 될 수도 있다. 그래서 반대로 transposed convolution과 spatial upsampling을 조합하기 보다는 일반적인 convolution과 upsampling을 조합하는 경우가 훨씬 많다. 먼저 작은 resolution이 있을 때 2배씩 upsampling을 통해서 크기를 키워주고 $3\times3$ 씩 convolution을 해서 값들을 하나씩 도출하여 차원을 유지하는 식으로 convolution을 적용할 수 있다. 정리하면 upsampling과 feature convolution을 조합해서 decomposition하여 사용하는 경우에는 transposed convolution 보다는 upsampling과 일반 convolution을 적용하는 경우가 더 많다.

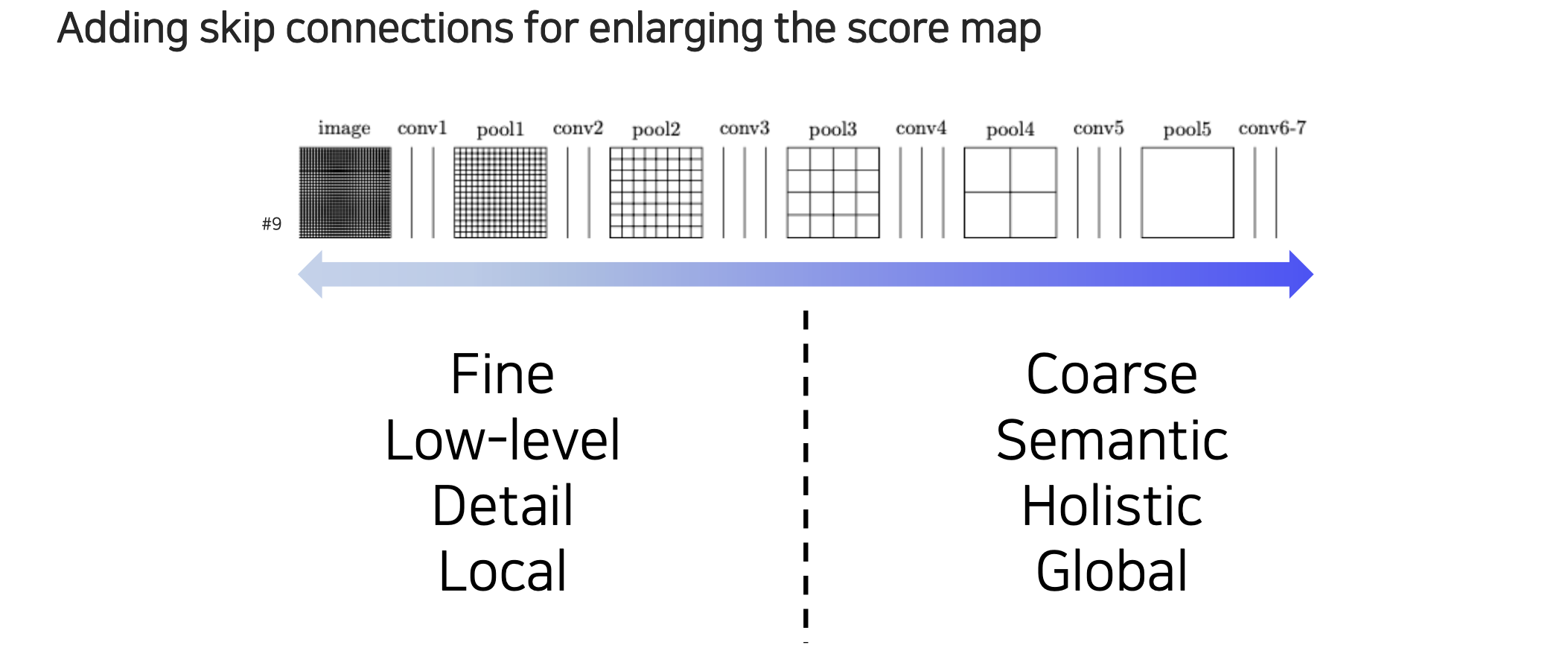우리가 $1\times1$ convolution을 이용해서 feature map을 다시 키우면서도 원래의 크기가 어떻게 들어오든 상관없이 동일한 resolution의 output을 출력할 수 있게 된다. 여기에 좀 더 semantic segmentation에 특화된 구조를 만들기 위해서 공학적인 디자인 원리를 적용시킬 수 있다. 하나의 관찰 포인트로는 skip connection을 추가해주는 것이다. Score map을 만들 때 low-resolution의 경우에는 영상의 전체적인 정보와 의미론적인 정보 등 전반적인 정보들을 포함하고 있는 것은 사실이지만 일단 영상이 너무 coarse해지는 문제가 있다. 그래서 여기에 upsampling을 하고 성능을 본다고 하더라도 경계선이 애매한 결과가 나올 것이다. 반대로 input단에서 보면 활용할 수는 없지만 경계선 등이 굉장히 잘 표현이 되어 있다. Convolution layer를 통한 결과만 보더라도 상대적으로 우측의 feature map 보다는 훨씬 resolution이 높으면서 디테일한 정보와 local 정보를 다 포함할 수 있다. 그저 단순하게 low-level의 정보들만 알고 있을 뿐이다. 좌측의 low-level에서는 털에 해당하고 눈에 해당하고 등의 지역적인 정보만 알 수 있다면 우측의 high-level에서는 고양이라는 전체적인 정보를 파악할 수가 있다.

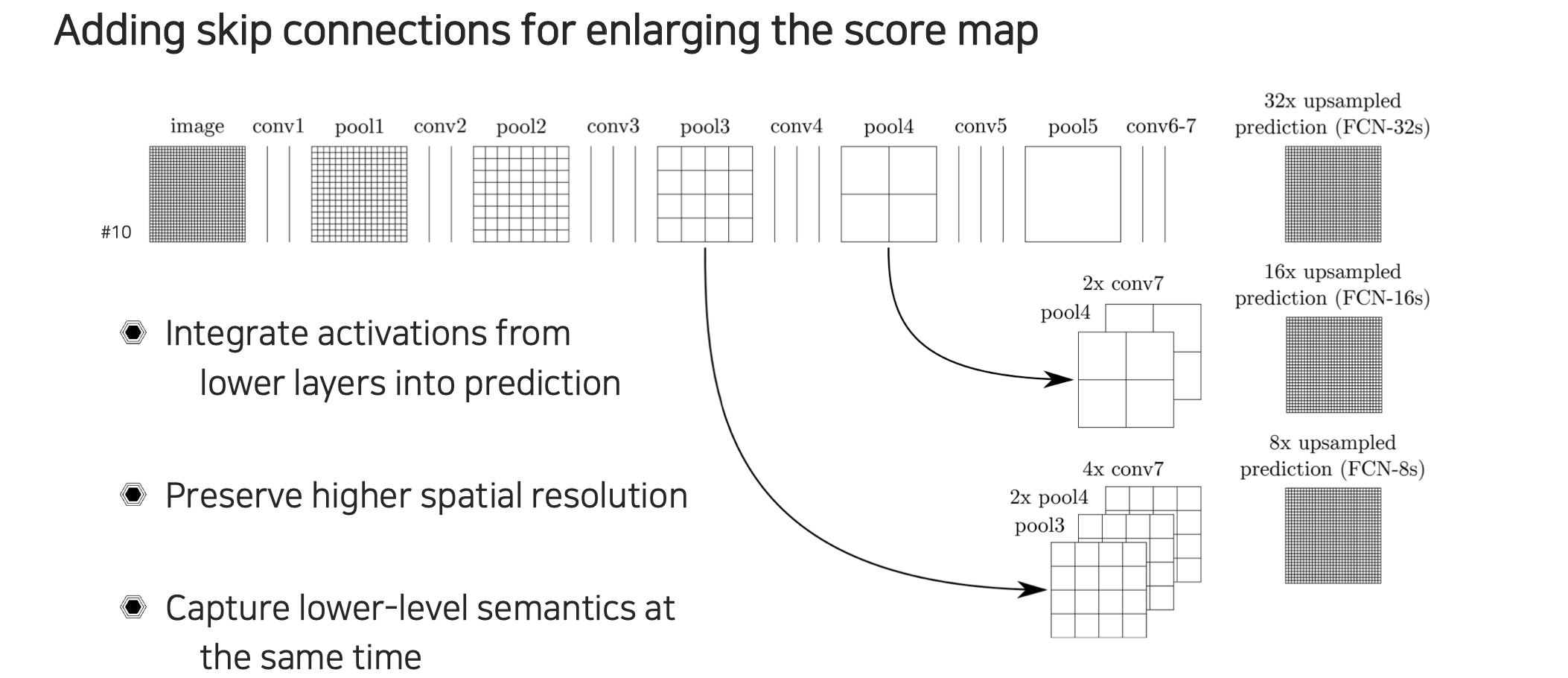Skip connection을 사용하면 low-level의 정보와 high-level의 정보를 상호보완적으로 사용할 수 있다. 위에서 보면 skip connection을 사용할 때 pool4 feature를 가져오고 마지막 conv7 feature도 가지고 와서 이를 16배 upsampling해서 사용하는 것을 FCN-16s라고 한다. 더 낮은 layer에서부터 feature를 가지고 오자는 것이 FCN-8s가 되는 것이다. Conv7에서 나온 feature map이 굉장히 low-resolution일텐데 이를 사용할 때에는 해당 feature map에 맞게 크기를 2배든 4배든 키워서 concatenation을 해서 사용하면 된다. 이렇게 하면 spatial resolution을 높게 가져갈 수 있고, low-level semantic뿐만 아니라 high-level semantic 정보도 동시에 고려할 수 있다.

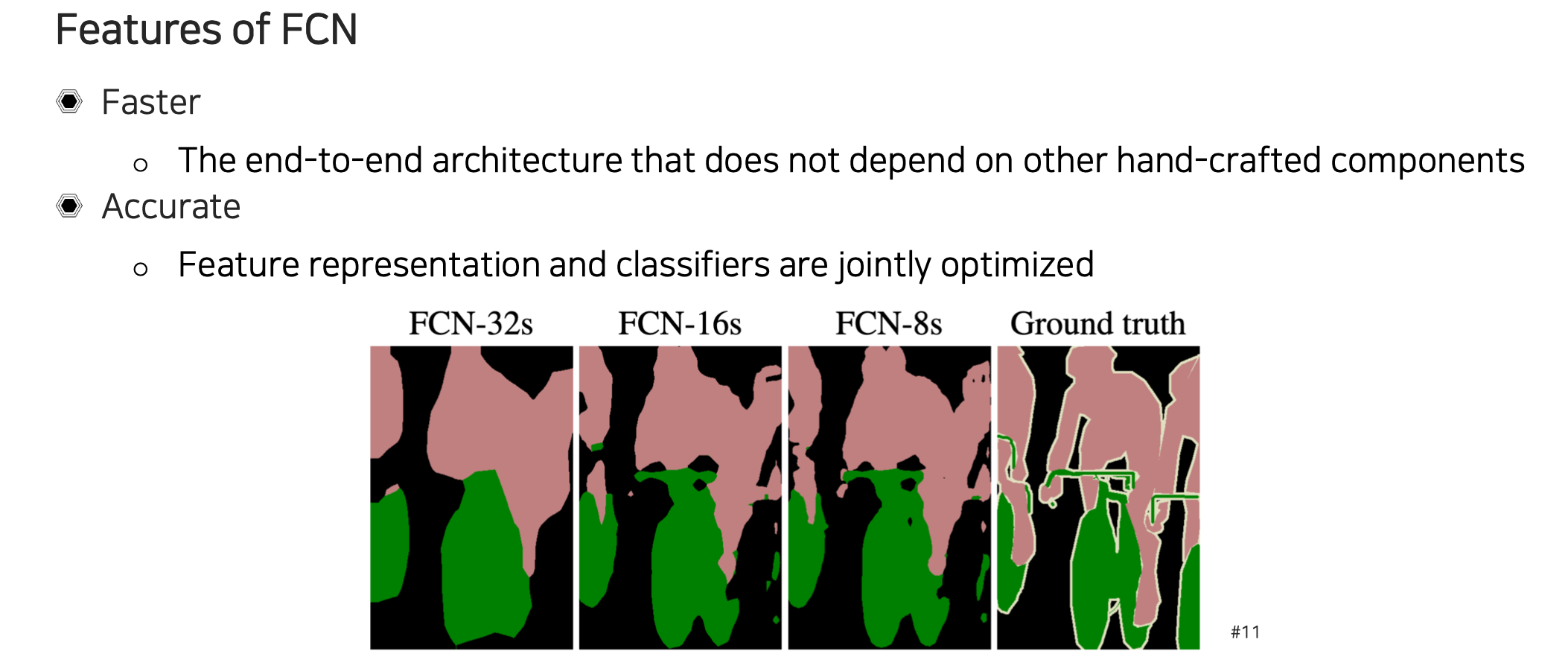결과를 비교해보면 마지막 layer만 32배 키워서 결과를 보았더니 결과가 좋지 않았다. 하지만 중간의 feature map을 함께 사용하게 되면 정교한 결과를 만들어낼 수가 있다.

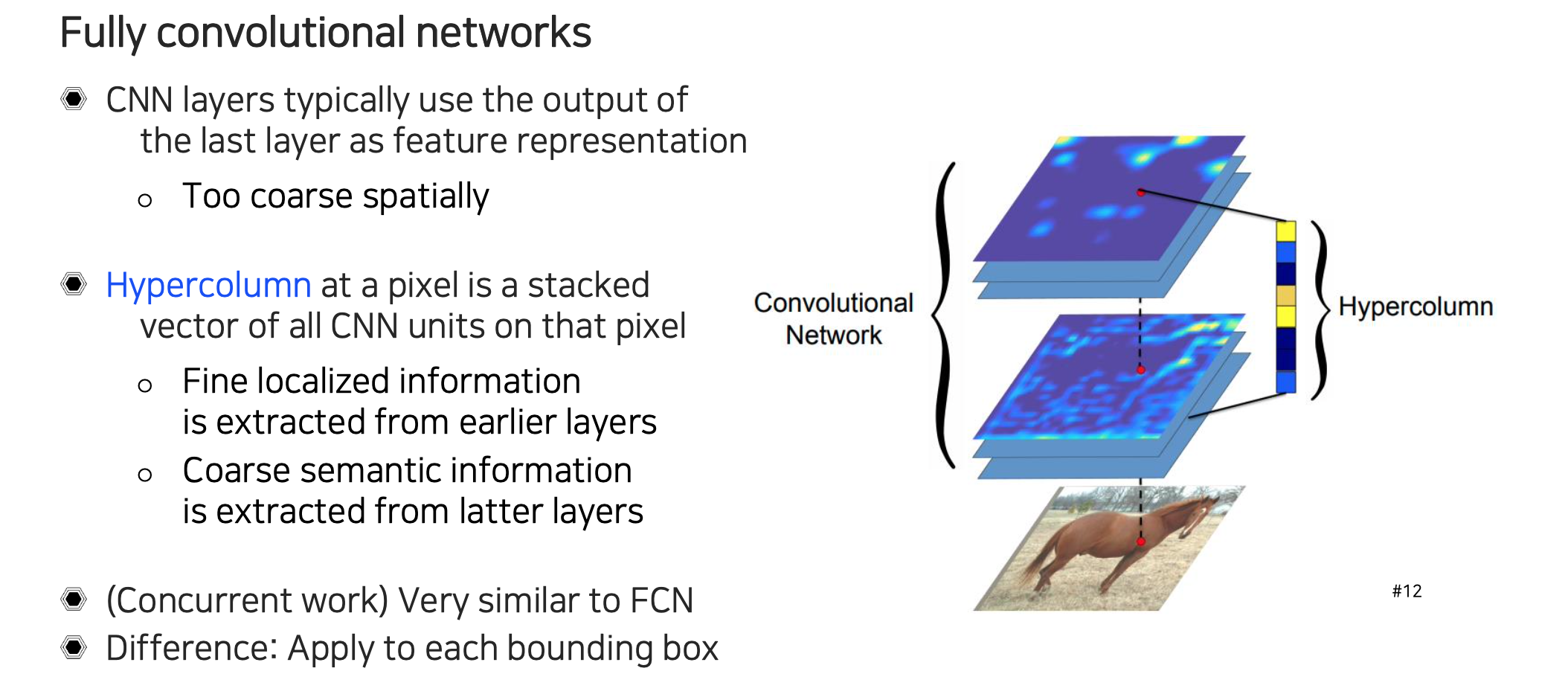2015년에 FCN이 나올 때 Hypercolumn이라는 연구도 함께 등장했다. 이 연구도 low layer와 high layer의 feature를 함께 뭉쳐서 사용하는 방식을 사용했다. 위쪽 feature map은 공간적으로 너무 coarse해서 high-level의 정보를 가지지만 정교한 resolution 정보를 가지지 못하고, 반대로 아래쪽 layer는 상대적으로 localization 정보는 잘 가지고 있지만 high level에서 semantic 정보는 가지지 못하는 한계가 있기 때문에 여러개의 layer를 concatenation해서 각 픽셀마다 feature vector라고 생각해서 사용하는 것이다. 결국 합쳐서 사용하기 위해서 high layer에 있는 feature map을 low layer에 있는 resolution에 맞추기 위해서 upsampling해서 쌓아주게 된다.