
이번에는 neural network를 학습할 때 사용할 수 있는 유용한 기법들과 전략에 대해서 알아보고자 한다. 특히, 이번에 알아보는 것은 한번만 setup해주면 바꾸지 않아도 되는 것들에 대해서 알아보려고 한다.
Activation functions
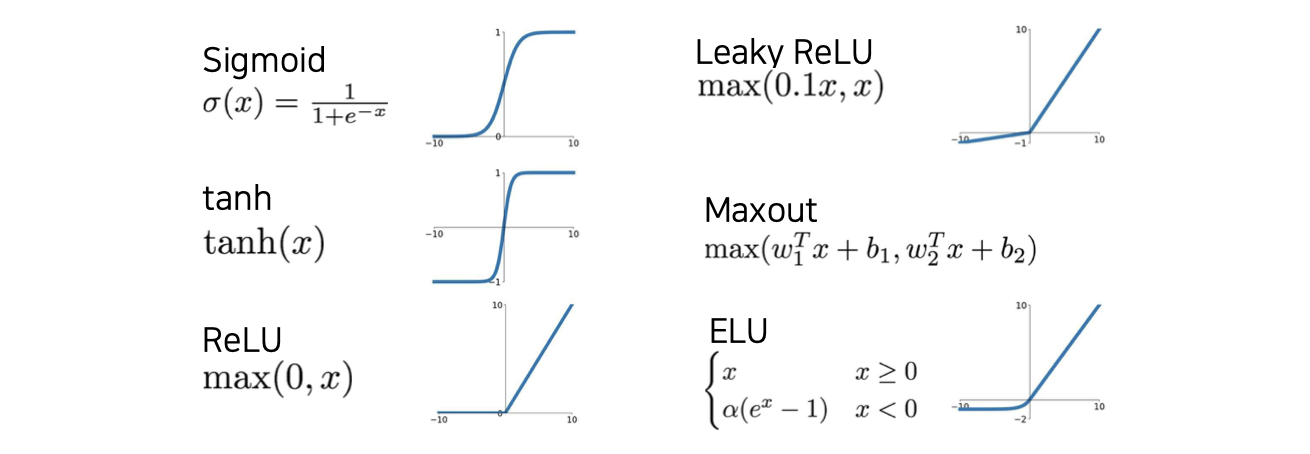 많은 activation function들이 도입되어 왔지만, ReLU의 등장으로 성능이 많이 향상이 되었다. 물론 지금도 sigmoid나 tanh를 사용하기는 한다. 그렇다면 어떠한 이유 때문에 ReLU가 성능을 많이 향상시킬 수 있었을까?
많은 activation function들이 도입되어 왔지만, ReLU의 등장으로 성능이 많이 향상이 되었다. 물론 지금도 sigmoid나 tanh를 사용하기는 한다. 그렇다면 어떠한 이유 때문에 ReLU가 성능을 많이 향상시킬 수 있었을까?
Sigmoid
 먼저 sigmoid function은 위와 같은 형태로, 어떠한 input이 들어와도 0에서 1사이로 mapping 시켜주게 된다. Neuron의 역치값을 넘으면 firing rate를 발생시키고 saturation까지 표현하는 다양한 특징 때문에 sigmoid를 역사적으로 많이 사용해왔다. 아무래도 sigmoid가 실제 생물학적으로 영감을 많이 받았기 때문이다.
먼저 sigmoid function은 위와 같은 형태로, 어떠한 input이 들어와도 0에서 1사이로 mapping 시켜주게 된다. Neuron의 역치값을 넘으면 firing rate를 발생시키고 saturation까지 표현하는 다양한 특징 때문에 sigmoid를 역사적으로 많이 사용해왔다. 아무래도 sigmoid가 실제 생물학적으로 영감을 많이 받았기 때문이다.
하지만 이러한 sigmoid를 neural network를 학습할 때 사용하면 크게 3가지 문제를 발생시킨다. 첫번째로 가장 중요한 문제로 gradient를 죽인다는 것이다. 다음 layer로 forward-propagation할 때 값이 너무 크거나 너무 작으면 back-propagation에서 sigmoid의 gradient가 0으로 수렴하게 된다. 그래서 값이 너무 커서 saturation 된 neuron의 경우 움직이지 않고 박혀버리게 되는 것이다.
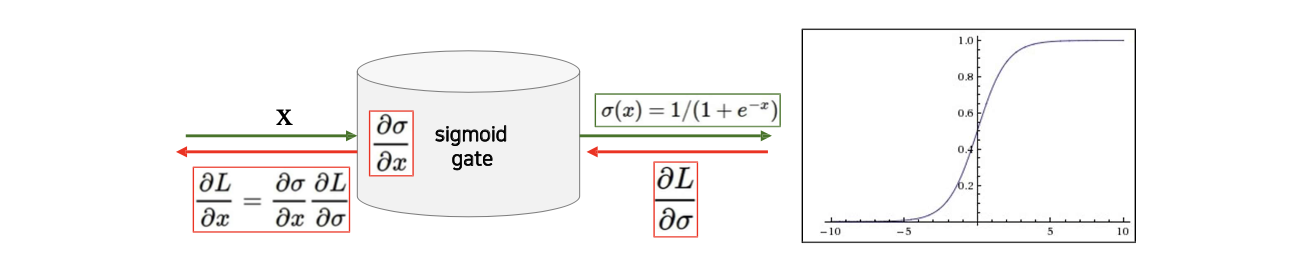 그래서 sigmoid의 gradient가 0이 되면 전부 0이 되어 값이 사라지게 된다. Gradient가 죽으면 상당히 큰 문제가 되는데, 두번째로는 sigmoid의 output이 zero-centered되지 않은 문제도 존재한다. Input이 어떠한 값이 되든 상관없이 sigmoid의 output이 양수에만 배치가 될 것이다.
그래서 sigmoid의 gradient가 0이 되면 전부 0이 되어 값이 사라지게 된다. Gradient가 죽으면 상당히 큰 문제가 되는데, 두번째로는 sigmoid의 output이 zero-centered되지 않은 문제도 존재한다. Input이 어떠한 값이 되든 상관없이 sigmoid의 output이 양수에만 배치가 될 것이다.
 이것이 문제가 되는 이유는 neuron의 input이 항상 양수가 된다는 것을 의미하게 된다. 그렇다면 input 가 양수가 되는 것이 왜 문제일까? 우리가 라는 parameter를 update할 때 일반적으로는 back-propagation을 사용한다. 이때 gradient가 에 대해서 어떻게 결정이 되는지 살펴볼 것이다.
이것이 문제가 되는 이유는 neuron의 input이 항상 양수가 된다는 것을 의미하게 된다. 그렇다면 input 가 양수가 되는 것이 왜 문제일까? 우리가 라는 parameter를 update할 때 일반적으로는 back-propagation을 사용한다. 이때 gradient가 에 대해서 어떻게 결정이 되는지 살펴볼 것이다.
 먼저 내부를 라고 생각하고, 를 에 대해서 미분을 취하게 되면 결과적으로 만 남게 될 것이다. 이때, 가 앞선 계산처럼 모두 양수라면 모든 에 대한 의 gradient가 양수가 됨을 의미하게 된다. 이는 을 에 대해서 미분을 취한 결과가 양수인지 음수인지에 따라서 전체적으로 모든 결과가 양수 혹은 음수로 결정이 될 것이다. 즉, 에 따라서 부호가 결정이 된다는 것을 의미한다. 우리가 weight가 2개라고 가정한다면 gradient는 항상 한쪽으로 zigzag 형태로 움직이게 된다. Gradient가 양수와 음수로 적당히 분배되어 움직이는게 아니라 모든 weight가 양수나 음수쪽으로 update되는 현상이 발생하게 될 것이다. 이렇게 되면 우리가 어느 지점에 도달해야 한다고 했을 때 직선으로 갈 수 있음에도 불구하고 converge가 굉장히 느려게 되어 성능이 확실하게 개선된다고 이야기하기 어려워질 것이다. 이러면 최적화 과정에서 악영향을 미치게 될 것이다. 여기서 data가 zero-mean을 가져야하는 이유도 설명이 된다.
먼저 내부를 라고 생각하고, 를 에 대해서 미분을 취하게 되면 결과적으로 만 남게 될 것이다. 이때, 가 앞선 계산처럼 모두 양수라면 모든 에 대한 의 gradient가 양수가 됨을 의미하게 된다. 이는 을 에 대해서 미분을 취한 결과가 양수인지 음수인지에 따라서 전체적으로 모든 결과가 양수 혹은 음수로 결정이 될 것이다. 즉, 에 따라서 부호가 결정이 된다는 것을 의미한다. 우리가 weight가 2개라고 가정한다면 gradient는 항상 한쪽으로 zigzag 형태로 움직이게 된다. Gradient가 양수와 음수로 적당히 분배되어 움직이는게 아니라 모든 weight가 양수나 음수쪽으로 update되는 현상이 발생하게 될 것이다. 이렇게 되면 우리가 어느 지점에 도달해야 한다고 했을 때 직선으로 갈 수 있음에도 불구하고 converge가 굉장히 느려게 되어 성능이 확실하게 개선된다고 이야기하기 어려워질 것이다. 이러면 최적화 과정에서 악영향을 미치게 될 것이다. 여기서 data가 zero-mean을 가져야하는 이유도 설명이 된다.
마지막 문제점으로는 exponential 연산이 들어가서 computationally expensive한 문제가 존재한다. 하지만 이 문제는 앞서 이야기한 두가지 문제점보다는 조금 더 minor한 문제에 해당하게 된다.
Tanh
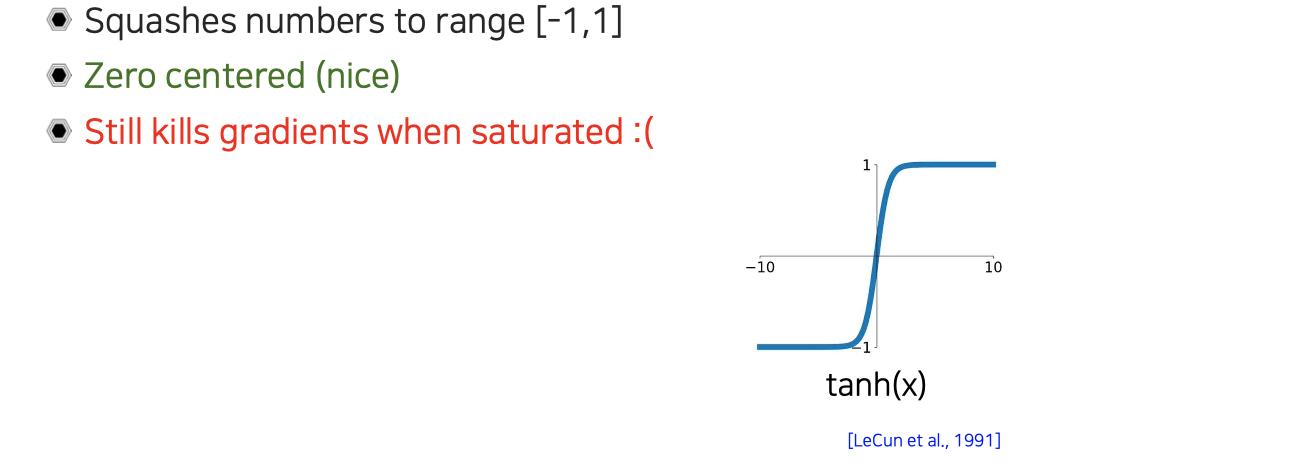 우리가 앞서 zero-centered 문제를 중요하게 생각했는데, 이를 해결하고자 도입된 activation function으로 tanh가 있다. Tanh는 -1에서 1로 mapping이 되어 있어서 zero-cented 문제를 해결할 수 있다. 하지만 여전히 saturation된 neuron에 대해서는 gradient가 vanishing되는 문제가 존재한다.
우리가 앞서 zero-centered 문제를 중요하게 생각했는데, 이를 해결하고자 도입된 activation function으로 tanh가 있다. Tanh는 -1에서 1로 mapping이 되어 있어서 zero-cented 문제를 해결할 수 있다. 하지만 여전히 saturation된 neuron에 대해서는 gradient가 vanishing되는 문제가 존재한다.
ReLU
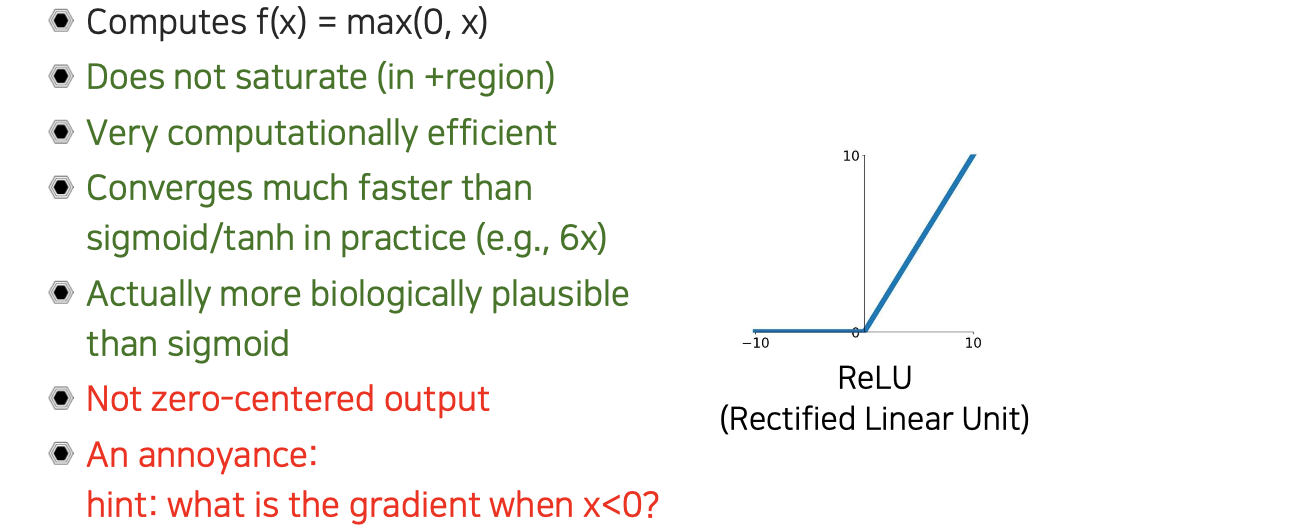 ReLU의 특징으로는 모든 영역에 대해서 saturation이 없어서 전부 양수가 되거나 0이 된다. 그래서 computation 관점에서 양수인지 음수인지만 구분하면 되서 효율적이다. 또한, 음수에서는 gradient가 0이고 양수일 때는 gradient가 linear하기 때문에 gradient vanishing 문제도 해결할 수 있다. Convergence 속도도 sigmoid나 tanh에 비해서 empirical하게 6배 정도 빠르다. 추가적으로 sigmoid보다 ReLU가 생물학적으로 더 맞다는 의견도 있다.
ReLU의 특징으로는 모든 영역에 대해서 saturation이 없어서 전부 양수가 되거나 0이 된다. 그래서 computation 관점에서 양수인지 음수인지만 구분하면 되서 효율적이다. 또한, 음수에서는 gradient가 0이고 양수일 때는 gradient가 linear하기 때문에 gradient vanishing 문제도 해결할 수 있다. Convergence 속도도 sigmoid나 tanh에 비해서 empirical하게 6배 정도 빠르다. 추가적으로 sigmoid보다 ReLU가 생물학적으로 더 맞다는 의견도 있다.
하지만 ReLU는 양수만 발생시켜 zero-centered 되어 있지 않은 문제가 존재하고, 음수가 input으로 들어왔을 때 gradient를 모두 죽여버리는 문제도 존재하게 된다.
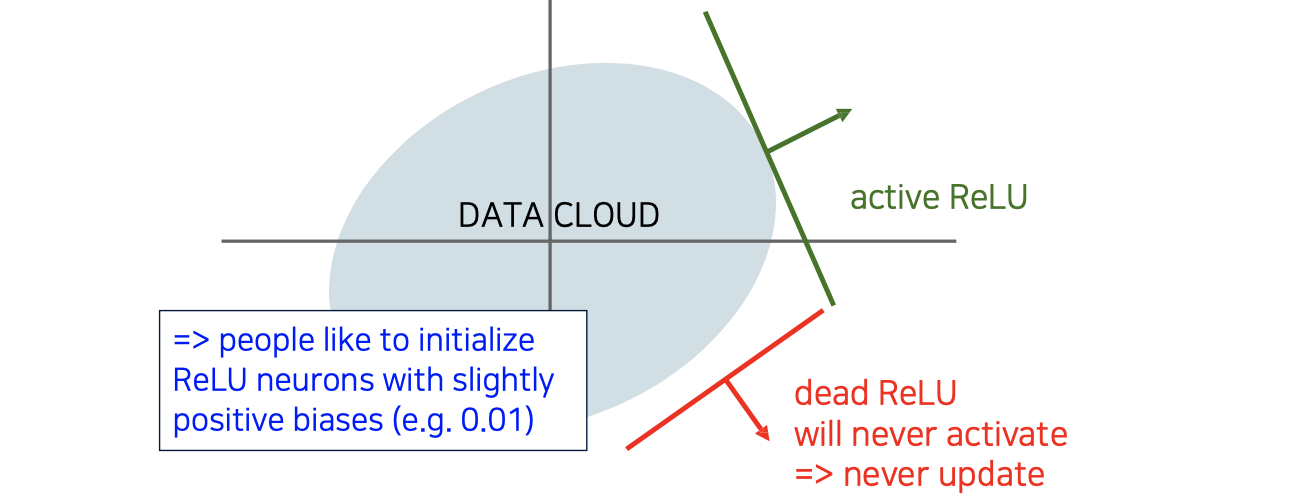 Gradient가 input이 음수일 때는 전혀 발생하지 않게 되는데, 위와 같이 data가 분포하고 있을 때 빨간선과 같이 ReLU가 형성이 된다면 모든 값이 음수가 되어 gradient를 전혀 발생하지 못하게 된다. 그렇게 되면 ReLU로 설정된 hyperplane도 바뀌지 않아 update 되는 parameter는 존재하지 않게된다. 만약 초록선과 같이 조금이라도 data 분포에 걸쳐있게 된다면 update가 될 것이다. 그래서 ReLU를 사용해서 initialization을 할 때에는 조금이라도 양수쪽에 걸쳐있도록 bias를 주어 사용하게 된다.
Gradient가 input이 음수일 때는 전혀 발생하지 않게 되는데, 위와 같이 data가 분포하고 있을 때 빨간선과 같이 ReLU가 형성이 된다면 모든 값이 음수가 되어 gradient를 전혀 발생하지 못하게 된다. 그렇게 되면 ReLU로 설정된 hyperplane도 바뀌지 않아 update 되는 parameter는 존재하지 않게된다. 만약 초록선과 같이 조금이라도 data 분포에 걸쳐있게 된다면 update가 될 것이다. 그래서 ReLU를 사용해서 initialization을 할 때에는 조금이라도 양수쪽에 걸쳐있도록 bias를 주어 사용하게 된다.
Leaky ReLU
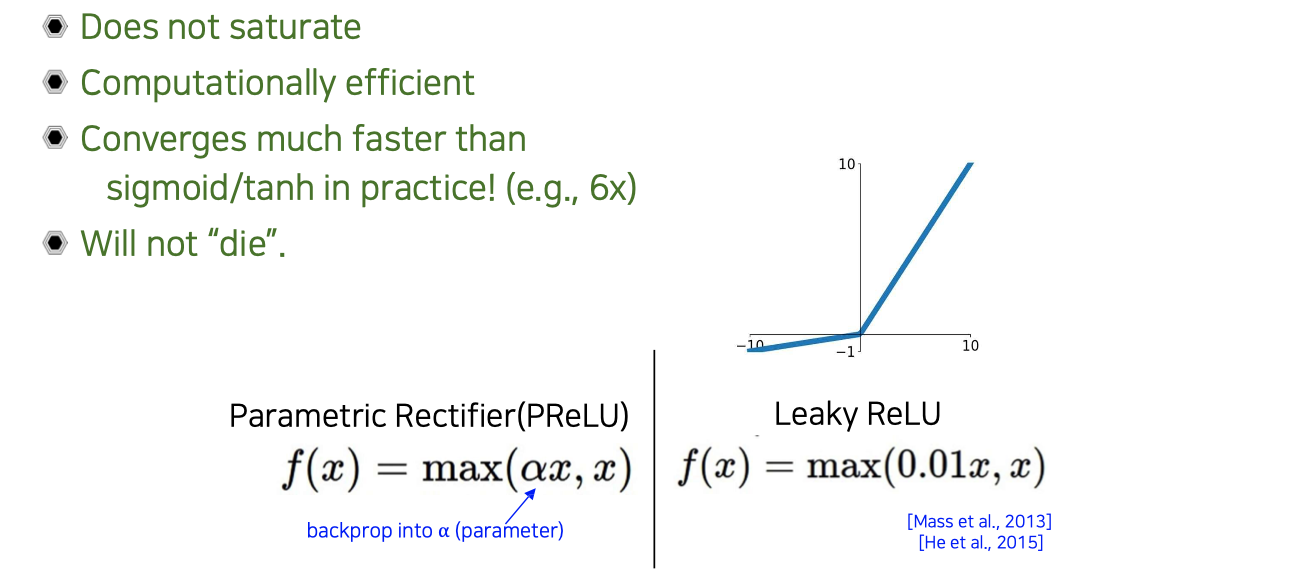 Input이 음수일 때 gradient가 사라지는 문제를 방지하기 위해서 Leaky ReLU라는 것이 도입되었다. 음수 쪽에서도 gradient가 0이 되지 않도록 조금 열어놓는 역할을 할 수 있다. Leaky ReLU 외에도 Parametric Rectifier(PReLU)라는 응용된 버전도 존재한다. 이는 음수쪽의 계수 를 back-propagation을 통해서 학습을 시키는 것으로, Leaky ReLU의 일반화 된 버전이다.
Input이 음수일 때 gradient가 사라지는 문제를 방지하기 위해서 Leaky ReLU라는 것이 도입되었다. 음수 쪽에서도 gradient가 0이 되지 않도록 조금 열어놓는 역할을 할 수 있다. Leaky ReLU 외에도 Parametric Rectifier(PReLU)라는 응용된 버전도 존재한다. 이는 음수쪽의 계수 를 back-propagation을 통해서 학습을 시키는 것으로, Leaky ReLU의 일반화 된 버전이다.
 실제로 practical하게는 ReLU를 굉장히 많이 사용할 것이다. 한가지 주의할 사항으로는 learning rate를 사용할 때 양수 쪽에는 bound가 되어 있지 않아서 굉장히 큰 값을 가질 수가 있기 때문에 learning rate를 잘 조절해서 explosion 되는 문제만 해결하면 된다. ReLU 외에도 Leaky ReLU나 Maxout, ELU와 같은 activation function도 사용해볼 수 있을 것이다. Tanh를 사용해도 되지만 주의할 사항이 존재하고, 이왕이면 sigmoid는 문제가 많아 사용하지 않는 것을 추천하는 편이다.
실제로 practical하게는 ReLU를 굉장히 많이 사용할 것이다. 한가지 주의할 사항으로는 learning rate를 사용할 때 양수 쪽에는 bound가 되어 있지 않아서 굉장히 큰 값을 가질 수가 있기 때문에 learning rate를 잘 조절해서 explosion 되는 문제만 해결하면 된다. ReLU 외에도 Leaky ReLU나 Maxout, ELU와 같은 activation function도 사용해볼 수 있을 것이다. Tanh를 사용해도 되지만 주의할 사항이 존재하고, 이왕이면 sigmoid는 문제가 많아 사용하지 않는 것을 추천하는 편이다.
Data preprocessing
우리가 layer를 지날때마다 input으로 양수만 들어오면 학습이 잘 안된다는 것을 이야기했는데, 실제로 data자체가 양수로만 존재해도 이와같은 이유로 학습이 잘 진행이 되지 않을 것이다. 대표적으로 image의 경우 0에서 255 사이의 값을 가지지만, 이를 0에서 1사이로 normalization 한다 하더라도 이와 같은 문제는 여전히 존재할 것이다.
 그래서 이러한 문제를 해결하기 위해서 PCA나 whitening과 같은 기법들을 적용하는 것이 고전 machine learning 문제에서 많이 사용되었다. Original data가 bias되어 있고 skew가 되어 있는 것을 위와 같이 decorrelation하고 whitening을 해서 data가 zero-centered 되게 만들고 covariance matrix도 identity matrix가 되도록 만들어주는 normalization을 많이 사용했었다.
그래서 이러한 문제를 해결하기 위해서 PCA나 whitening과 같은 기법들을 적용하는 것이 고전 machine learning 문제에서 많이 사용되었다. Original data가 bias되어 있고 skew가 되어 있는 것을 위와 같이 decorrelation하고 whitening을 해서 data가 zero-centered 되게 만들고 covariance matrix도 identity matrix가 되도록 만들어주는 normalization을 많이 사용했었다.
 실제로는 PCA와 같은 기법들을 잘 사용하지 않는다. AlexNet의 경우에는 mean image를 구해서 data에서 평균값만 빼서 사용했다. Sigma나 variance같은 것을 normalization하지 않아도 0으로 평균만 맞춰줘도 성능이 어느정도 잘 나오는 것을 보여주었다. VGGNet에서는 mean image를 만들 필요 없이 각 채널로부터 전체적인 평균값을 빼서 zero-centered 형태로 만들기만 해도 효과적임을 보여주었다. 그래서 image에서는 실제로 center normalization만 진행해주었다.
실제로는 PCA와 같은 기법들을 잘 사용하지 않는다. AlexNet의 경우에는 mean image를 구해서 data에서 평균값만 빼서 사용했다. Sigma나 variance같은 것을 normalization하지 않아도 0으로 평균만 맞춰줘도 성능이 어느정도 잘 나오는 것을 보여주었다. VGGNet에서는 mean image를 만들 필요 없이 각 채널로부터 전체적인 평균값을 빼서 zero-centered 형태로 만들기만 해도 효과적임을 보여주었다. 그래서 image에서는 실제로 center normalization만 진행해주었다.
Batch normalization
 중간의 feature level에서 zero-centered 특성을 어떻게 만들지에 대해서 대표적인 성공 사례인 batch normalization에 대해서 알아보고자 한다. Batch normalization에서 하고싶은 것은 중간 activation이 zero-mean이 되고 unit-variance를 가지면 좋지 않을까라는 motivation으로부터 등장했다. 중간층에 있는 activation의 한 batch를 고려하게 되는데, batch라는 것이 적당한 개수의 data로 모여있는 형태이다 보니까 그 내에서 statistics를 구해서 normalization을 하고자 하는 것이다. 그래서 normalization은 batch 내에서의 평균과 표준편차를 구해서 각 data를 zero-mean unit-variance로 normalization 해주는 것이다.
중간의 feature level에서 zero-centered 특성을 어떻게 만들지에 대해서 대표적인 성공 사례인 batch normalization에 대해서 알아보고자 한다. Batch normalization에서 하고싶은 것은 중간 activation이 zero-mean이 되고 unit-variance를 가지면 좋지 않을까라는 motivation으로부터 등장했다. 중간층에 있는 activation의 한 batch를 고려하게 되는데, batch라는 것이 적당한 개수의 data로 모여있는 형태이다 보니까 그 내에서 statistics를 구해서 normalization을 하고자 하는 것이다. 그래서 normalization은 batch 내에서의 평균과 표준편차를 구해서 각 data를 zero-mean unit-variance로 normalization 해주는 것이다.
 Batch normalization을 적용할 때에는 위와 같이 차원의 data가 개로 하나의 batch를 이루고 있을 때 개의 data의 각 채널마다 indepandent하게 평균과 표준편차를 구해서 normalization 후에 사용하게 된다.
Batch normalization을 적용할 때에는 위와 같이 차원의 data가 개로 하나의 batch를 이루고 있을 때 개의 data의 각 채널마다 indepandent하게 평균과 표준편차를 구해서 normalization 후에 사용하게 된다.
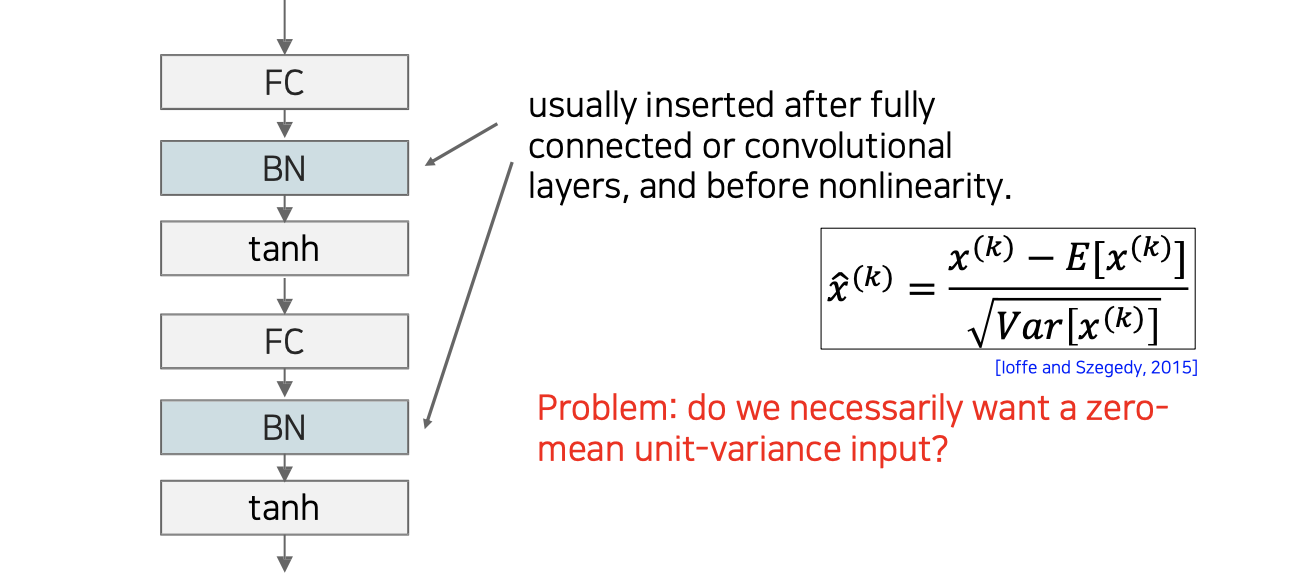 Batch normalization은 보통 FC layer와 activation function 중간에 사용이 된다. 꼭 이렇게 정해진 것은 아니고 어떠한 형태를 사용하는지에 따라 activation function 이후에 사용하기도 한다. 하지만 일반적으로는 FC layer나 convolution layer 다음에 non-linearity 이전에 사용하게 된다.
Batch normalization은 보통 FC layer와 activation function 중간에 사용이 된다. 꼭 이렇게 정해진 것은 아니고 어떠한 형태를 사용하는지에 따라 activation function 이후에 사용하기도 한다. 하지만 일반적으로는 FC layer나 convolution layer 다음에 non-linearity 이전에 사용하게 된다.
하지만 정말로 activation function이 zero-mean unit-variance input을 원한다고는 이야기할 수 없다. 이 부분에 대해서는 network가 자체적으로 학습할 수 있으면 좋겠다고 고려할 수도 있다. Activation function이 항상 zero-centered 되어 있는 것이 좋다고 이야기할 수는 없는 것이다.
 그래서 normalization 이후에 새로운 offset과 scale parameter를 다시 곱해줘서 range를 recovery를 해주는 것이다. 이렇게해서 network에 더 적합한 statistics를 가질 수 있도록 유도해주게 된다. 여기서 offset 와 scaling factor 는 learnable parameter로 network에 input으로 들어온 원래의 statistics도 커버할 수 있다보니까 적어도 identity mapping 정도는 recover할 수 있는 능력을 가지고 있게 된다. 그래서 결과적으로 이러한 방법이 기존의 statistis를 보정할 수 있는 일반적인 방법으로 볼 수 있다.
그래서 normalization 이후에 새로운 offset과 scale parameter를 다시 곱해줘서 range를 recovery를 해주는 것이다. 이렇게해서 network에 더 적합한 statistics를 가질 수 있도록 유도해주게 된다. 여기서 offset 와 scaling factor 는 learnable parameter로 network에 input으로 들어온 원래의 statistics도 커버할 수 있다보니까 적어도 identity mapping 정도는 recover할 수 있는 능력을 가지고 있게 된다. 그래서 결과적으로 이러한 방법이 기존의 statistis를 보정할 수 있는 일반적인 방법으로 볼 수 있다.
 위는 batch normalization을 하는 algorithm을 정리한 것이다. 각 layer마다 layer 내에서 평균과 분산에 대한 statistics를 구하고 normalization을 해준 후에 다시 scaling과 offset을 더해줌으로써 새로운 statistics를 입혀주게 된다. 이렇게 되면 network가 target task를 수행하는데 더 적합한 형태로 적응시켜줄 수 있다. 다르게 이해하면 zero-mean과 unit-variance를 가지는 것 자체도 사람들의 고정 관념이 될 수가 있는데, 이로부터 벗어나 network가 더 좋은 성능을 가질 수 있도록 하면 좋겠다는 디자인 철학이 담긴 것이다.
위는 batch normalization을 하는 algorithm을 정리한 것이다. 각 layer마다 layer 내에서 평균과 분산에 대한 statistics를 구하고 normalization을 해준 후에 다시 scaling과 offset을 더해줌으로써 새로운 statistics를 입혀주게 된다. 이렇게 되면 network가 target task를 수행하는데 더 적합한 형태로 적응시켜줄 수 있다. 다르게 이해하면 zero-mean과 unit-variance를 가지는 것 자체도 사람들의 고정 관념이 될 수가 있는데, 이로부터 벗어나 network가 더 좋은 성능을 가질 수 있도록 하면 좋겠다는 디자인 철학이 담긴 것이다.
그래서 이렇게 batch normalization을 사용하면 gradient flow가 좋아지며, learning rate도 더 큰 값을 사용할 수 있게 된다. 그리고 initialization을 어떻게 하는지에 따라 성능이 많이 바뀔 수가 있는데, batch normalization을 통해서 여기에 대한 의존성을 많이 줄여줄 수 있게 된다. 더불어 중간중간 normalization이 어떻게보면 regularization과 같은 효과라고 생각할 수도 있다. 그래서 다른 dropout과 같이 다른 regularization 방법을 중복 사용해야 하는 필요성도 많이 낮춰줄 수가 있다.
 Test에 batch normalization을 사용해야 할 때에는 training과는 조금 다르기 때문에 이 부분을 조금 주의할 필요가 있다. 실제 구현에서는 batch 자체로 inference를 하지 않고, sample 각각을 inference하는 경우도 많다. Sample이 하나만 주어지면 평균과 분산을 구하는 것이 불가능하다. 그래서 inference할 때 평균과 분산을 계산하지 못하기 때문에 empirical한 평균과 분산을 미리 저장해놓게 된다. 그 방법은 학습 도중에 running average를 통해서 dataset 전체에 대한 평균값을 batch를 매번 돌면서 estimation하고, empirical한 분산값도 미리 estimation 해놓는 것이다. 이렇게 training sample들로부터 구해놓은 평균과 분산을 inference에 가져다가 사용하는 것이다. 그리고 학습시에 batch의 크기를 1로 사용하는 경우도 존재하는데, 이때는 평균과 표준편차를 제대로 구할 수 없기 때문에 batch normalization을 하면 안된다.
Test에 batch normalization을 사용해야 할 때에는 training과는 조금 다르기 때문에 이 부분을 조금 주의할 필요가 있다. 실제 구현에서는 batch 자체로 inference를 하지 않고, sample 각각을 inference하는 경우도 많다. Sample이 하나만 주어지면 평균과 분산을 구하는 것이 불가능하다. 그래서 inference할 때 평균과 분산을 계산하지 못하기 때문에 empirical한 평균과 분산을 미리 저장해놓게 된다. 그 방법은 학습 도중에 running average를 통해서 dataset 전체에 대한 평균값을 batch를 매번 돌면서 estimation하고, empirical한 분산값도 미리 estimation 해놓는 것이다. 이렇게 training sample들로부터 구해놓은 평균과 분산을 inference에 가져다가 사용하는 것이다. 그리고 학습시에 batch의 크기를 1로 사용하는 경우도 존재하는데, 이때는 평균과 표준편차를 제대로 구할 수 없기 때문에 batch normalization을 하면 안된다.
Weight initialization
만약 weight를 initialization한다고 했을 때 constant로 하게 되면 어떻게 될까?
 Weight를 전부 constant로 시작하면 gradient를 update하는 과정에서 큰 문제가 발생한다. 이 문제가 발생했을 때 회피하는 방법으로는 random한 숫자를 만들어서 할당할 수 있을 것이다. 그래서 zero-mean Gaussian을 사용해서 위와 같이 initialization을 할 수 있을 것이다. 이렇게 하면 작은 network에서는 적당히 작동하게 된다. 하지만 network가 커지게 되면 문제가 발생하게 된다. 예를 들어 위와 같이 10개의 layer를 사용하는 예시에서 forward-propagation하는 중간에 존재하는 hidden layer의 activation의 statistics 값들을 우리는 확인해볼 수 있을 것이다.
Weight를 전부 constant로 시작하면 gradient를 update하는 과정에서 큰 문제가 발생한다. 이 문제가 발생했을 때 회피하는 방법으로는 random한 숫자를 만들어서 할당할 수 있을 것이다. 그래서 zero-mean Gaussian을 사용해서 위와 같이 initialization을 할 수 있을 것이다. 이렇게 하면 작은 network에서는 적당히 작동하게 된다. 하지만 network가 커지게 되면 문제가 발생하게 된다. 예를 들어 위와 같이 10개의 layer를 사용하는 예시에서 forward-propagation하는 중간에 존재하는 hidden layer의 activation의 statistics 값들을 우리는 확인해볼 수 있을 것이다.
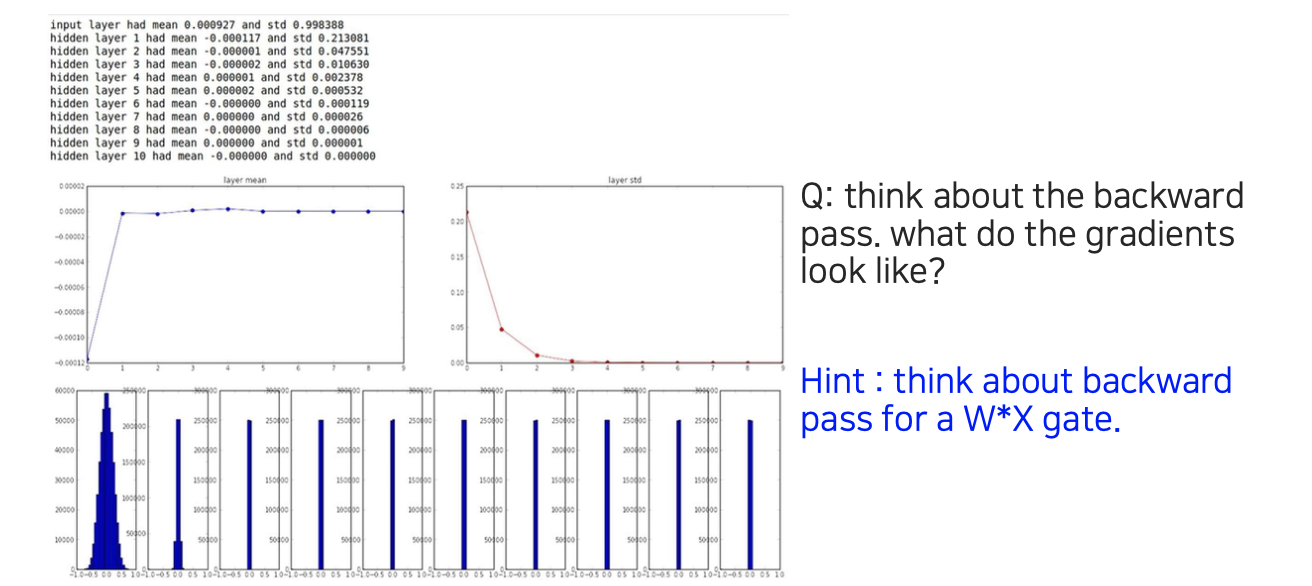 그 결과는 위와 같으며 layer가 깊어질수록 표준편차는 0에 수렴하는 것을 볼 수 있다. Activation의 평균을 보면 처음에는 어딘가 bias되어 있지만 0에 계속 모여있는 것을 확인할 수 있다. 높은 확률로 backward-propagation에서 가 activation 값이 되는 경우가 많을 것이다. 근데 이 값들이 전부 0이라는 이야기다. 그러면 결과적으로 gradient vanishing 문제를 발생시킬 것이다. 그래서 대부분의 activation 값이 0이되는 것은 큰 문제가 된다.
그 결과는 위와 같으며 layer가 깊어질수록 표준편차는 0에 수렴하는 것을 볼 수 있다. Activation의 평균을 보면 처음에는 어딘가 bias되어 있지만 0에 계속 모여있는 것을 확인할 수 있다. 높은 확률로 backward-propagation에서 가 activation 값이 되는 경우가 많을 것이다. 근데 이 값들이 전부 0이라는 이야기다. 그러면 결과적으로 gradient vanishing 문제를 발생시킬 것이다. 그래서 대부분의 activation 값이 0이되는 것은 큰 문제가 된다.
 우리는 여기서 0.01 대신에 1.0과 같이 큰 값을 곱해줄 수 있을 것이다. 하지만 이렇게해도 여전히 문제는 발생하게 된다. 우리의 예시에서는 tanh를 사용했기 때문에 곱해지는 weight들이 축적이 되어 계속 커지게 될 것이다. 1보다 큰 값이 계속 곱해지게 되면 결국 saturation이 될 것이다. 그래서 위와 같이 각 layer에서 statistics가 -1과 1로 전부 saturation 되어 버리고, 그렇게되면 tanh의 경우에 gradient를 구하면 전부 0이 될 것이다. 이렇게 해도 결국에는 gradient vanishing 문제가 발생하는 것이다. 결국 너무 작은 값들을 계속 곱해도 문제지만 너무 큰 값들을 곱해도 문제가 되는 것이다. 우리는 initialization의 중요성을 여기서 다시 생각해볼 수 있다.
우리는 여기서 0.01 대신에 1.0과 같이 큰 값을 곱해줄 수 있을 것이다. 하지만 이렇게해도 여전히 문제는 발생하게 된다. 우리의 예시에서는 tanh를 사용했기 때문에 곱해지는 weight들이 축적이 되어 계속 커지게 될 것이다. 1보다 큰 값이 계속 곱해지게 되면 결국 saturation이 될 것이다. 그래서 위와 같이 각 layer에서 statistics가 -1과 1로 전부 saturation 되어 버리고, 그렇게되면 tanh의 경우에 gradient를 구하면 전부 0이 될 것이다. 이렇게 해도 결국에는 gradient vanishing 문제가 발생하는 것이다. 결국 너무 작은 값들을 계속 곱해도 문제지만 너무 큰 값들을 곱해도 문제가 되는 것이다. 우리는 initialization의 중요성을 여기서 다시 생각해볼 수 있다.
Xavier initialization
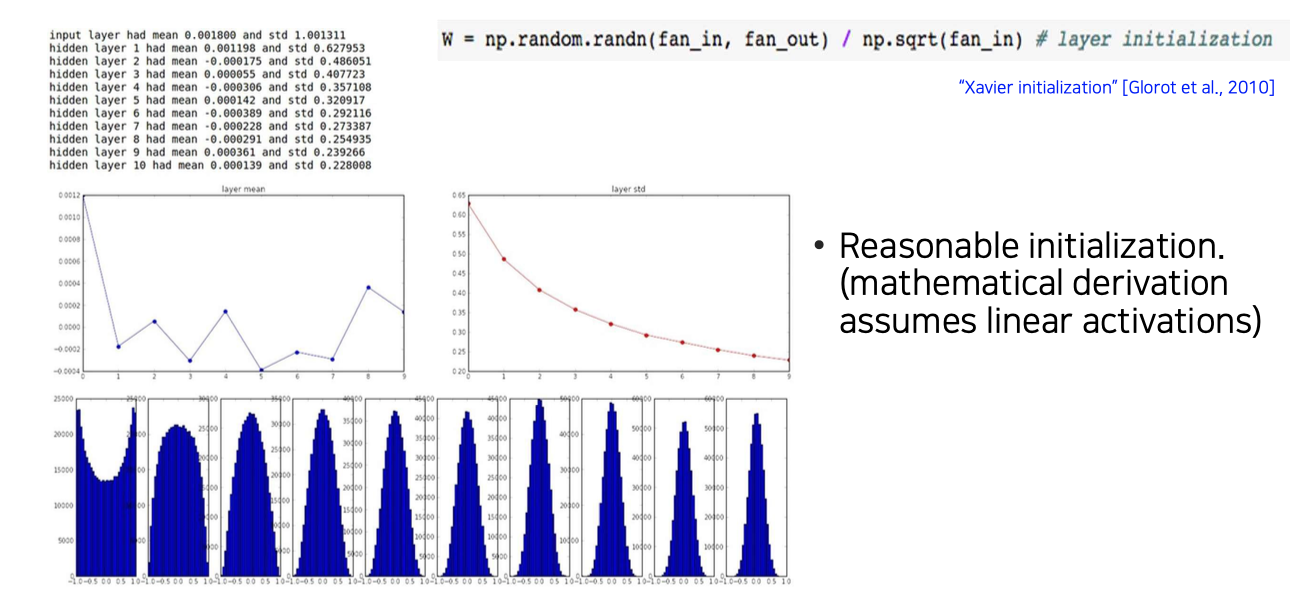 이러한 문제를 해결하고자 Xavier initialization이 도입되었다. 적당한 parameter 설정을 어떻게 해줄지에 대해서 제시한 대안이다. Input 차원에 root를 취해서 적용해주는 것이 적절한 initialization이 되는 결과를 가져온 것이다.
이러한 문제를 해결하고자 Xavier initialization이 도입되었다. 적당한 parameter 설정을 어떻게 해줄지에 대해서 제시한 대안이다. Input 차원에 root를 취해서 적용해주는 것이 적절한 initialization이 되는 결과를 가져온 것이다.
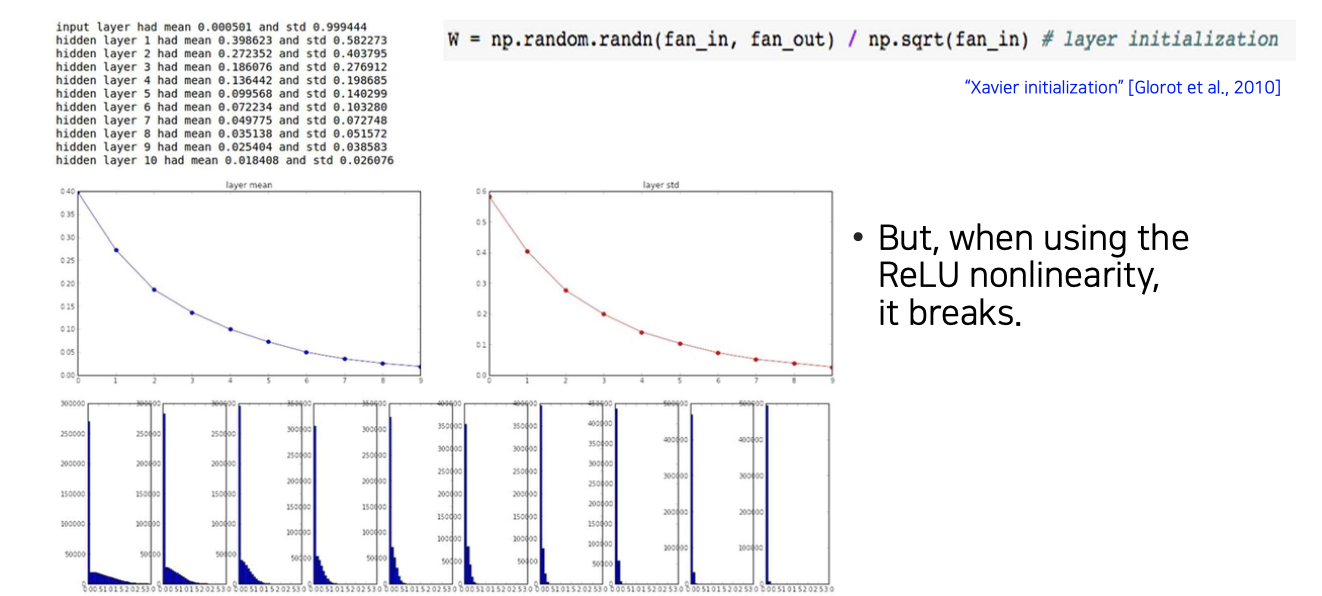 하지만 여기서 문제는 Xavier initialization의 경우 유도 과정에서 중간에 non-linear activation이 없고 linear activation을 가정하고 유도했다. 그러다보니 ReLU를 사용하는 경우에는 Xavier initialization의 좋은 성질들이 없어지게 되는 것이다. ReLU의 특성상 대부분 activation 값들이 0을 가지게 된다. 그러다보면 상위 layer에서 모든 값들이 0이 되면 back-propagation이 불가능해지게 된다.
하지만 여기서 문제는 Xavier initialization의 경우 유도 과정에서 중간에 non-linear activation이 없고 linear activation을 가정하고 유도했다. 그러다보니 ReLU를 사용하는 경우에는 Xavier initialization의 좋은 성질들이 없어지게 되는 것이다. ReLU의 특성상 대부분 activation 값들이 0을 가지게 된다. 그러다보면 상위 layer에서 모든 값들이 0이 되면 back-propagation이 불가능해지게 된다.
He initialization
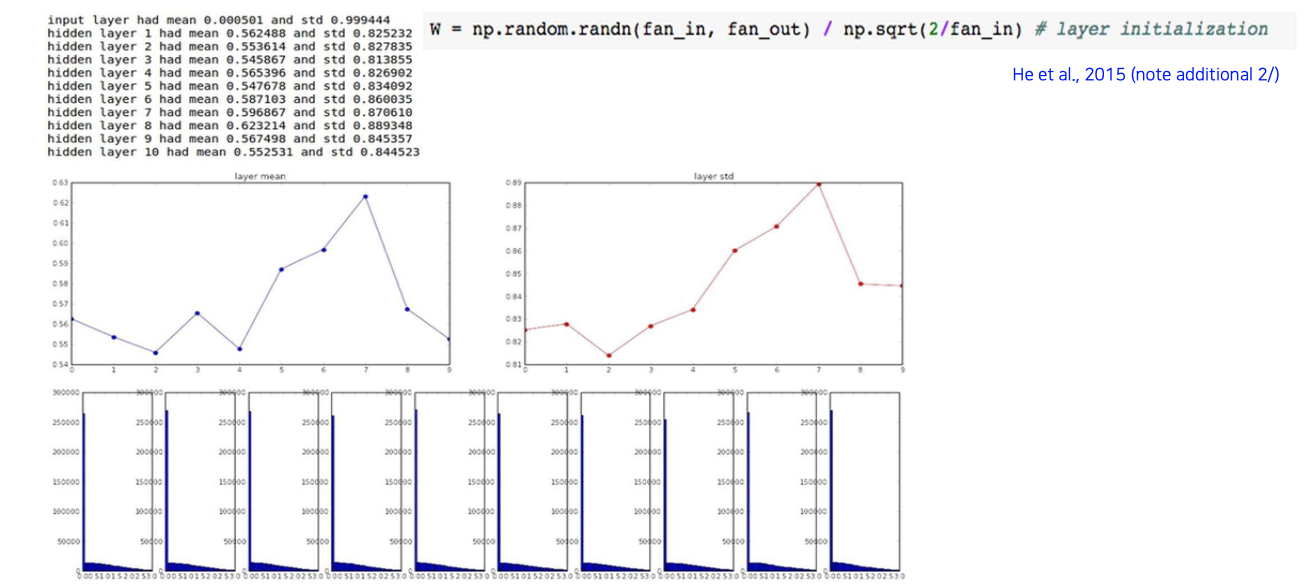 그래서 이를 해결하고자 He initialization이 도입이 되었다. 여기서는 ReLU 상태일 때 scaling factor를 어떻게 설정하면 좋을지를 유도했더니 위와 같이 distribution이 잘 유지되는 것을 확인할 수 있었다.
그래서 이를 해결하고자 He initialization이 도입이 되었다. 여기서는 ReLU 상태일 때 scaling factor를 어떻게 설정하면 좋을지를 유도했더니 위와 같이 distribution이 잘 유지되는 것을 확인할 수 있었다.
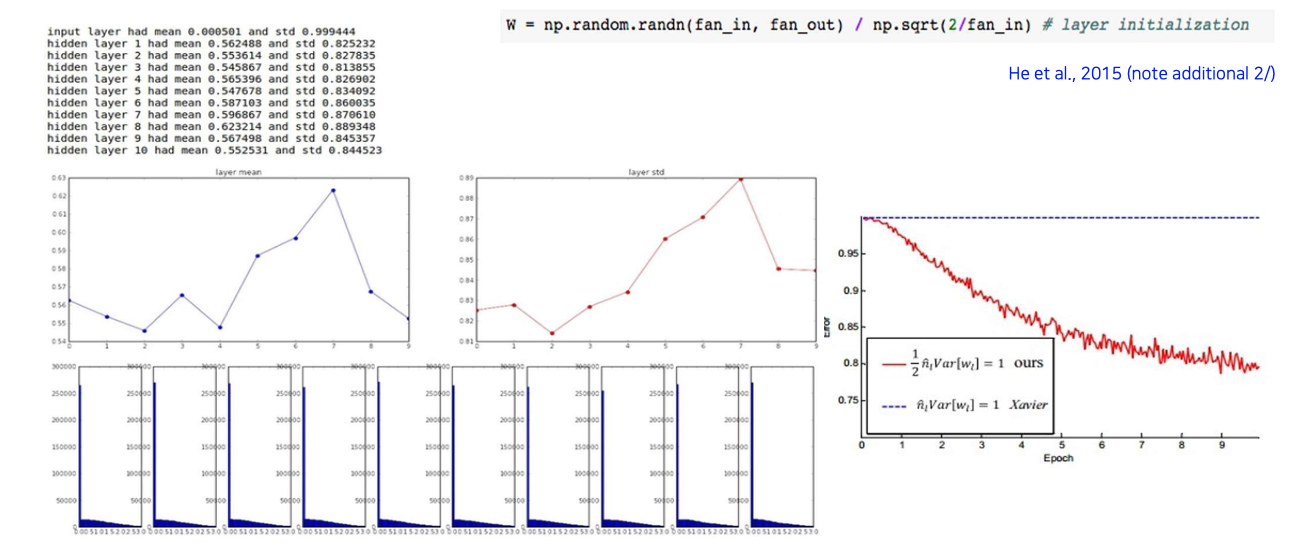 Training 과정에서도 Xavier initialization과의 차이를 확인해볼 수 있었다.
Training 과정에서도 Xavier initialization과의 차이를 확인해볼 수 있었다.
