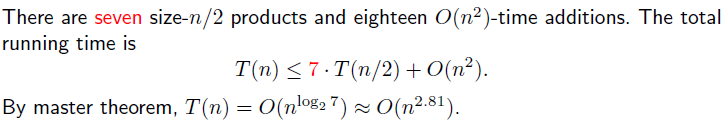행렬 곱셈(Matrix Multiplication)
두 n * n 행렬인 X와 Y의 곱셈 Z의 (i, j)번째 값은 다음과 같다.
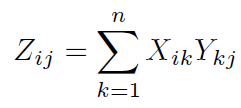이를 행렬 표현으로 시각적으로 표현하면, Z의 (i, j)번째 값은 X의 i번째 행(row)와 Y의 j번째 열(column)의 내적(dot product)이다.
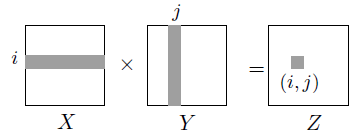행과 열이 모두 n이고 내적하는 단계에서 선형적 시간이 필요하기 때문에 이 알고리즘의 수행시간은 O(n3)이다. 이 방법은 널리 알려졌으며, 더 나은 알고리즘은 없다는 것이 기정사실화 되었지만, 1969년에 독일 수학자 폴커 스트라센(Volker Strassen)이 분할정복법에 기반한 상당히 효율적인 알고리즘을 발표했다.
행렬 곱셈은 부분 문제로 나누기 쉬운데, 그 이유는 행렬이 블록 단위로 수행될 수 있기 때문이다. 다음과 같이하나의 행렬을 4개의 블록으로 나누는 것이 가능하다.
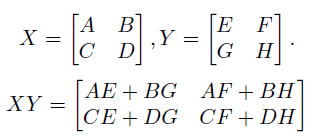Master theorem을 이용하기 위해 위 방법은 8개의 크기가 n / 2인 AE, BG, AF, BH, CE, DG, CF, DH를 재귀적으로 계산하기에 branching factor인 a는 8이 되고, 크기를 절반으로 줄였기에 b는 2가 된다. 추가적인 덧셈 시간이 O(n2)이 필요해서 d는 2가 된다. 그래서 이 알고리즘의 수행 시간은 다음과 같다.
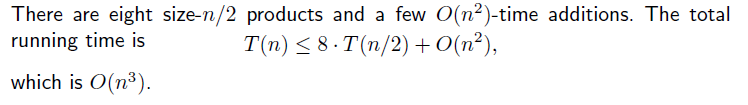이 수행 시간은 기존 알고리즘과 같기에 왜 효율적인지 의문이 들 수 있다. 하지만 여기서 교묘하게 식의 변형을 통해서 수행 시간을 더 효율적으로 만들 수 있다.
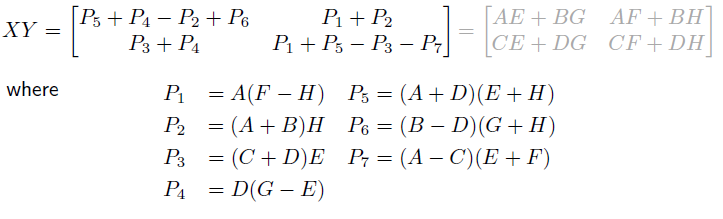이렇게 식을 변형하면 XY에서 8개의 곱셈과 덧셈이 필요했던 것에서 이제는 7개의 곱셈과 덧셈으로 바꿀 수 있다. 이렇게 되었을 때 새로운 수행 시간은 다음과 같으며, 이는 더욱 개선된 것을 확인할 수 있다.
