Shortest Paths in Graphs
그래프의 node는 무수히 많이 존재할 수 있고, 이에따라 이를 연결하는 edge들도 많이 존재할 수 있다. 이때, 우리는 특정한 node 2개를 골라 이들 사이의 최단 거리를 구하고 싶은 경우가 존재할텐데, 이때의 최단 거리를 distance라고 한다. 다음의 그래프를 예를 들 것이고 S와 C 사이의 distance를 구해볼 것이다.
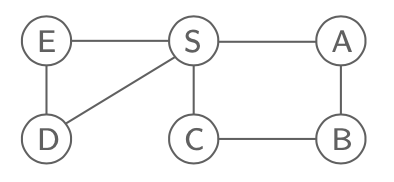간단한 그래프이며, 이때의 distance는 S와 C가 바로 연결되어 있기 때문에 1이 될 것이다. 그럼 조금 다른 형태의 그래프를 예로 들어보자.
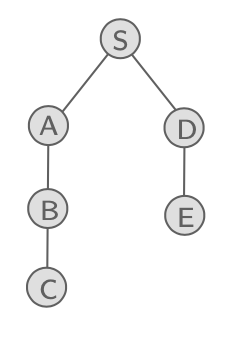이 그래프는 위의 그래프를 약간 변형시킨 그래프이다. 이 그래프에서 S로부터 C까지의 distance를 구하기 위해서 DFS를 이용한다고 했을 때,우리는 A, B를 차례로 지나야한다. 그러면 이 경우에 대해서는 distance가 3이 될 것이지만, 매번 우리는 DFS를 이용하여 distance를 구하는데에는 한계가 존재할 것이다. 가령 depth가 심한 그래프의 경우 경제적으로 효과적인 search를 하지 못하기 때문이다. 그렇기 때문에 shortest path를 찾기 위해서는 모든 그래프에서 통용되는 경제적인 알고리즘이 필요하다.
Dijkstra's Algorithm
DFS의 효율적인 측면 때문에 unit length를 가지는 어떠한 그래프에서 shortest path를 찾는데는 BFS가 더 효율적이다. 그렇다면 만약에 edge가 unit length가 아닌 positive integer length를 가지게 된다면 어떠할 것인가? 즉, node와 node 사이에는 1 이상의 어떠한 정수 값을 가지고 있는 것이다. 다음의 예시를 통해서 BFS가 제대로 동작하는지 확인해보고 싶다.
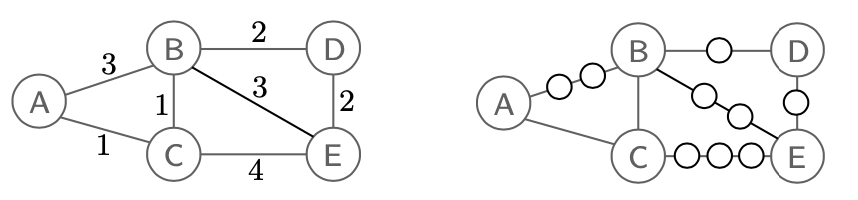BFS는 정상적으로 동작할 것이다. 하지만 만약에 정수 값이 매우 큰 edge들이 존재하게 된다면, BFS도 이러한 edge들 때문에 경제적으로 비효율적일 수 있다.
Alarm Clock Algorithm
이를 해결해보고자 alarm이라는 개념을 도입해서 계산을 할 것이다. 우선 시작할 지점의 node의 alarm 값을 0으로 설정하고(alarm(s) = 0), 도착할 지점의 나머지 node들의 alarm 값을 무한대로 설정한다(alarm(v) = ∞). 그 다음에는 더이상 남은 alarm이 없을 때 까지 alarm 값을 바꿔주는 것을 반복하면 된다. 이때 우리는 도착 지점의 node의 이전 alarm 값과 계속 더해져온 alarm 값에 직전 edge length를 더한 값 중에서 더 적은 값으로 alarm 값을 업데이트 해줄 것이다. 이러한 alarm clock 알고리즘을 통해서 양의 정수값을 가지는 edge들이 존재하는 어떠한 그래프에서든지 distance를 계산할 수 있다.
Dijkstra's Algorithm code
그리고 이를 이용하여 다익스트라 알고리즘을 code로 작성하면 다음과 같다.
이러한 alarm clock을 사용하는 알고리즘은 heap을 통한 priority queue를 사용하게 되며, 이 code를 해석하고 알고리즘을 이해하기 위해서 간단하게 예시를 들어가며 설명해보겠다.
Dijkstras Algorithm Example
시작 node는 A로 설정할 것이고, 우리가 하고 싶은 것은 A로부터 나머지 node들 까지의 distance를 구하는 것이다. 이를 위해서 다익스트라 알고리즘이 어떻게 동작하는지 차근차근 볼 것이다. 그리고 A로부터 다른 node까지의 거리는 dist(x)로 표기할 것이고 시작할 때 모든 dist 값은 ∞으로 시작한다.
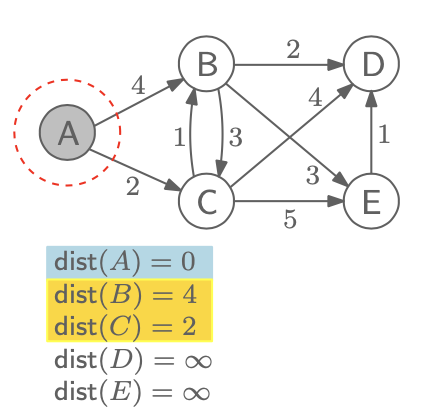A가 시작점이기 때문에 dist(A) = 0이 되며, 이 값은 이제 저장이 되어 변하지 않을 것이다. 그리고 바로 근접한 B와 C의 distance는 바로 edge값이 되어 dist(B) = 4, dist(C) = 2가 된다. 바로 값을 정했지만, 알고리즘대로 한다면 이전의 값과 비교하여 더 적은 값으로 업데이트를 하는 것이기 때문에 무한대보다는 무조건 적은 값이라 바로 업데이트를 한 것이다. 여기서 핵심은 근접한 node들까지의 거리만 구하고 나머지 distance는 업데이트를 하지 않은채 다음 단계로 넘어가는 것이다.
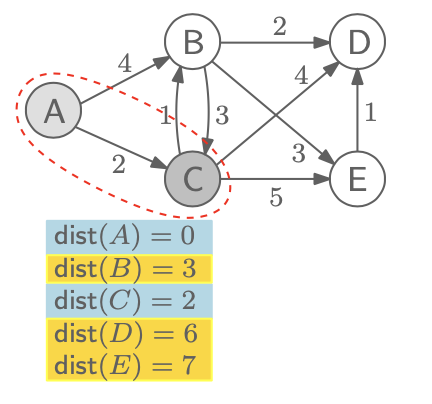다음으로 지정할 node는 C이다. 그 이유는 가장 적은 dist 값을 가지는 node를 기준으로 해야 최소한의 값들로 업데이트를 할 수 있기 때문이다. A는 값이 정해졌기 때문에 C와 이웃한 B, D, E의 값을 이전의 값들과 비교하여 더 적은 값으로 바꿔 줄 것이다. dist(B)는 이전 값이 4였지만, C를 지나가는 것을 기준으로 했을 때 2(dist(C)) + 1 = 3이 되어 4 > 3이기 때문에 dist(B) = 3으로 업데이트 해준다. 그리고 dist(D)는 C를 기준으로 2 + 4 = 6이 되고 이는 무한대보다 적기 때문에 바로 업데이트 해준다. dist(E)도 마찬가지로 2 + 5 = 7로 업데이트 해준다.
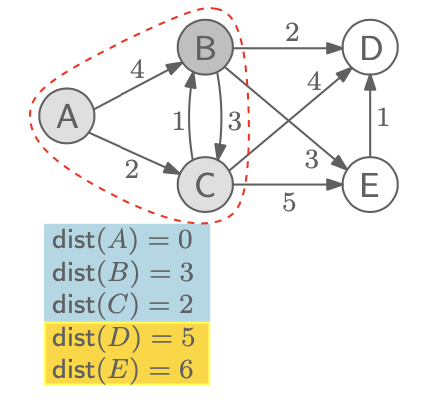다음으로 지정할 node는 B이다. dist 값이 3으로 가장 적기 때문이다. 이 상태로 이웃한 dist(D) 값을 업데이트 해줄 것인데, dist(B)인 3과 2를 더한 5와 기존의 dist(D) 값인 6이랑 비교했을 때 5가 더 적기 때문에 dist(D) = 5로 업데이트 해준다. dist(E)도 마찬가지로 3 + 3 = 6 < 7 이기 때문에 dist(E) = 6이 된다.
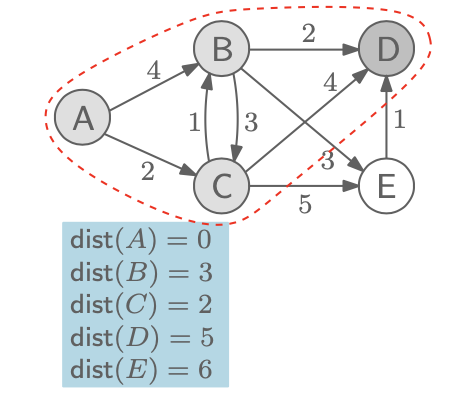이제 남은 node들 중에서 D를 기준으로 보았을 때, E로 향하는 edge가 없어서 다익스트라 알고리즘은 여기서 마치게 되고, A로부터의 최단 거리가 전부 정해지게 되었다. 그리고 이 값들을 이용해서 필요한 edge만 표기하면 다음과 같다.
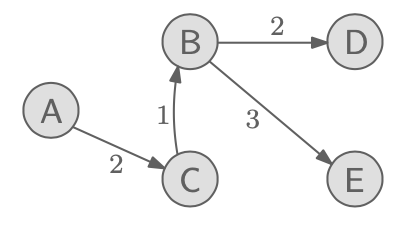
우리가 이 방식에서 자세히보면 값을 업데이트 할 때, 최단 dist값을 가지는 node를 기준으로 계속해서 업데이트 해왔는데, 이 방법이 정말 보장된 방법인 것인지 궁금해할 수 있다. 만약 다른 node를 지나가서 더 적은 값이 생기지 않을까 하는 의문이 있을 수 있는데, 이는 걱정할 필요가 없다.
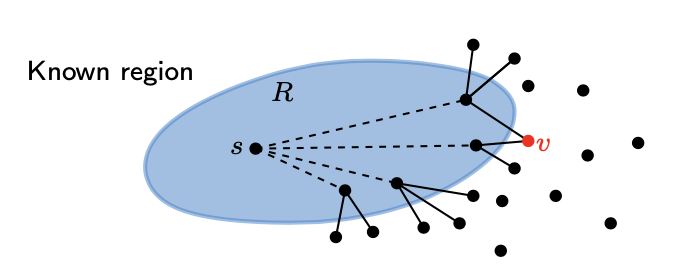시작 지점부터 계속해서 적은 값으로 업데이트를 해왔다면, 결국 마지막에 따져야할 것은 원하는 도착 지점 직전의 edge값만 따져주면 된다. 다른 edge들을 통해서 오는 것은 이미 값이 더 클 것이다.
Dijkstra's Algorithm Running Time
다익스트라 알고리즘은 구조적으로 BFS와 동일하다. 하지만, 이는 BFS보다 속도적으로 느린데, 그 이유가 priority queue의 구조를 사용하기 때문이다. 값을 eject하고 inject하는데 constant time이 소요되는 BFS와 달리, 다익스트라 알고리즘은 컴퓨터적으로 더 많은 계산을 요구하게 된다.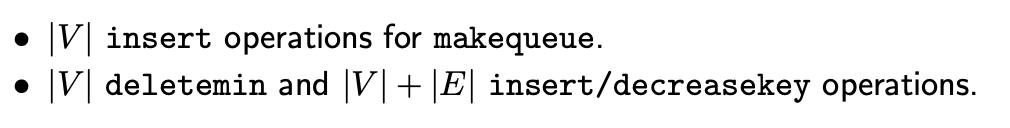 
물론 priority queue를 사용할 수도 있는거지만, 만약 데이터를 다루는데 다른 array나 binary heap 등을 사용할 수도 있는 것이다. 어떠한 데이터 structure을 사용하는가는 사용하는 사람의 취향이 따르겠지만, 이왕이면 효율적으로 돌아가는 것이 알고리즘을 작성하는데 더 좋을 것이다.
