[확률통계] Joint Probability, Marginal Probability, Conditional Probability

이번에는 확률을 좀 더 확장한 개념들로, 결합 확률, 주변 확률, 그리고 조건부 확률에 대해서 알아보고자 한다. 어느정도 고등학교 확률 시간에 배운 개념들이므로 그리 어렵지 않게 이해할 수 있을 것이다. 그래서 지금부터는 여러 개의 확률 변수를 종합하여 생각해 볼 것이다.

Joint Probability

결합 확률(Joint probability)은 2개의 사건이 동시에 일어나는 확률을 말한다. 우리는 고등학교를 다니면서 "∩"이라는 기호를 자주 보았을 것이다. 결합 확률은 이 기호를 사용하여 나타내면 된다. 그래서 서로 다른 2개의 사건 A와 B가 일어났을 때, 이 2개의 사건이 동시에 일어나는 확률이 결합 확률이고, 이를 P(A∩B) 로 표기할 수 있다.
다른 방식으로도 나타낼 수 있으며, 이 방식이 좀 더 많이 사용될 것이다. 확률 변수 X와 Y에 대해서 X = a이고, Y = b가 성립 될 확률을 P(X = a, Y = b) 라고 표기할 것이며, 이렇게 여러 조건을 지정하고 모든 조건이 동시에 성립하는 확률을 또한 결합 확률이라고 한다.

Marginal Probability

주변 확률(Marginal probability)은 개별 사건의 확률을 말하는데, 결합 확률과 대비해서 P(X = a) 나 P(Y = b) 와 같은 단독 확률을 주변 확률이라고 한다.
그리고 결합 확률과 주변 확률의 관계는 다음과 같이 나타낼 수 있다.
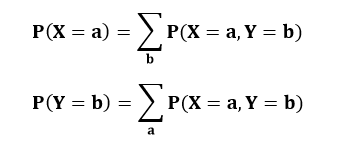아마 이렇게 식으로 보면 잘 이해가 되지 않을 수 있다. 그래서 간단한 예시를 들어보려고 한다.
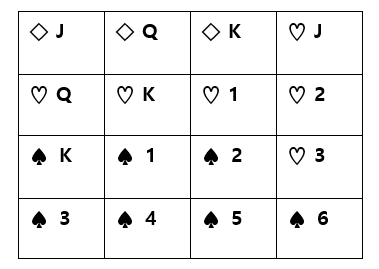위와 같이 하얀색 카드와 검정색 카드가 있으며, 각각의 카드에는 숫자와 문자가 적혀 있다. 이를 이용해서 우선 결합 확률을 구해보고자 한다.
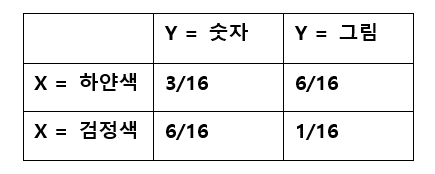확률 변수 X를 색깔, Y를 글자라고 하였을 때, 위와 같이 X와 Y에 공통적으로 해당하는 카드의 개수를 세어 결합 확률로 나타낸 표이다. 그리고 이를 각각의 개별 사건에 대한 확률인 주변 확률을 구해보면 다음과 같이 구하면 된다.
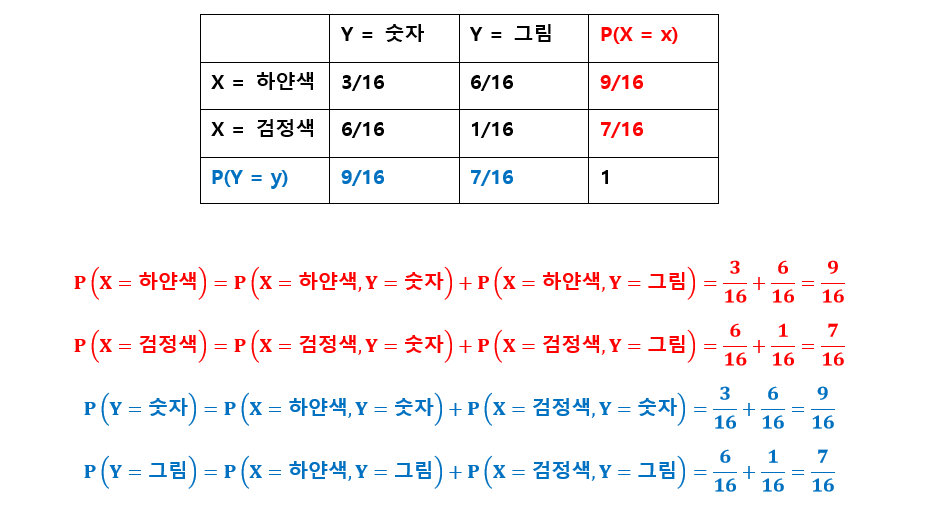예시를 통해서 보면, 이제 위에 관계식에 대해서는 이해가 쉽게 되었을 것이다.

Conditional Probability

조건부 확률(Conditional probability)은 특정한 주어진 조건 내에서 어떠한 사건이 발생할 확률을 말한다. 즉, 조건부 확률은 어떤 사건 A가 일어났다는 전제 하에서 다른 사건 B가 발생할 확률이고, 이를 P(B | A) 라고 표기할 수 있다.
위의 예시를 이용해서 설명해보려고 한다. 우리가 원하는 카드는 이제 'X = 하얀색'의 경우로 한정하려고 한다. 하얀색 카드가 9장이 있는데, 이 중에서 삼분의 일은 숫자가 적혀 있고, 나머지 삼분의 이는 그림이 그려져 있다. 이를 다음과 같이 조건부 확률로 표기할 수 있다.
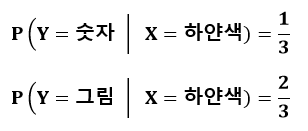그리고 이를 X = 하얀색이라는 조건 하에서 Y = 숫자 카드일 조건부 확률은 1/3, X = 하얀색이라는 조건 하에서 Y = 그림 카드일 조건부 확률은 2/3라고 말하면 된다. 즉, 여기서 X = 하얀색이라는 조건하에서의 Y의 조건부분포를 구한 것이다.

Joint, Marginal, Conditioanl Probabilitiy의 관계

우리는 위에서 구한 조건부 확률을 일반적으로 쓰면 다음과 같이 식을 적을 수 있다.
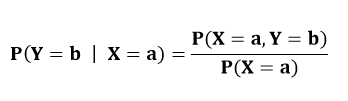이것이 바로 조건부 확률의 정의이다. 위에서 배운 결합 확률과 주변 확률을 이용해서 나타낸 것을 알 수 있는데, 이는 정의상 그럴 수 밖에 없다.
그리고 결합 확률의 합은 1이 되어야 하는데, 이는 위에서 표를 통해서 다 더해보면 1이 되는 것을 쉽게 확인할 수 있다.

추가로 우리는 3개 이상의 확률 변수에 대해서도 이처럼 조건부 확률을 정의할 수 있다.
많이 복잡해 보일 수는 있지만, 지금까지 설명한 내용에서 특별히 비약한 것은 없다. 모두 단순히 조건과 조건이 복합적으로 된 것이다. 그리고 이러한 복잡한 형태도 일반적으로 다음과 같이 분해할 수 있다는 것을 알아두면 좋다.

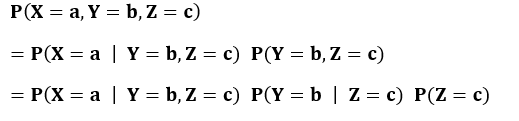
공학적인 측면에서 조건부 확률은 주목받을 때가 많다. 어떤 문제를 규명하면 '어떤 X가 이런 값이었을 때, 다른 어떤 Y는 이런 값이 된다'는 관계를 둘러싼 이야기에 이르기 때문이다. 그러나 현실에서는 노이즈가 많이 섞여 들어오는 것을 피할 수 없기 때문에 완벽하게 정확히 측정하기란 불가능하다. 그래서 X의 측정치가 같다고 해도 얻는 Y의 측정치는 달라져 버린다. 그렇기 때문에 조건부 확률을 많이 논하게 되는 것이다.