Introduction
이번 과제는 2개의 문제로 이루어져 있다.
1.규제화를 사용한 모델 학습
<Softmax Regression.ipynb에 있는 코드를 수정해서 다음을 구현해보세요.>
1-1. L2 regularization을 비용함수(compute_cost 내에)에 포함시키고 gradient 계산에(batch_gd 내에) 반영하세요.
1-2. Regularization을 위한 가중치 lambda를 튜닝해보세요. 이것을 위해서 학습데이터의 일부를 validation data로 따로 구분하고 이 validation data에 대한 accuracy를 최적화하는 lambda를 찾도록 하는 코드를 구현해보세요.
2.다중클래스 분류모델의 결정경계 구하기
<아래 웹페이지에서 두 가지의 모델이 학습됩니다. 각각의 모델이 가지는 결정경계를 나타내는 방정식들을 구하고 화면에 나타내보세요.>
https://scikit-learn.org/stable/auto_examples/linear_model/plot_logistic_multinomial.html
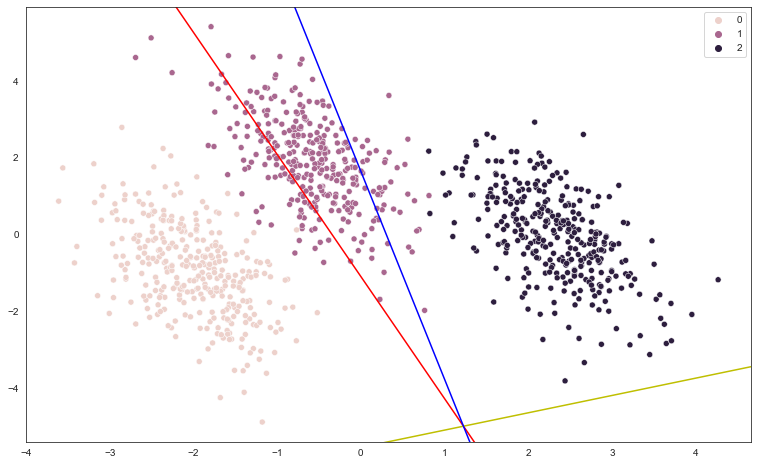
아래 이미지처럼 한 모델의 결정경계는 세 개의 직선방정식으로 나타낼 수 있습니다. 즉, 클래스1과 클래스2의 경계를 나타내는 직선방정식, 클래스1과 클래스3의 경계를 나타내는 직선방정식 그리고 클래스2와 클래스3의 경계를 나타내는 직선방정식입니다. 방정식들을 구하고 화면에 그려보세요.
문제 해결 과정과 obstacles
L2 Regularization
Softmax Regression.ipynb 파일을 살펴보면 mnist_784 데이터를 사용해 숫자를 구분하는 logistic regression의 코드가 만들어져 있음을 알 수 있다.
데이터 처리 과정을 생략하고 핵심 코드를 살펴보면
활성함수로 softmax함수를 사용하고 있으며
def sigmoid(x):
return 1 / (1 + np.exp(-x))def softmax(X, W):
K = np.size(W, 1)
A = np.exp(X @ W)
B = np.diag(1 / (np.reshape(A @ np.ones((K,1)), -1)))
Y = B @ A
return Y손실함수를 다음과 같이 계산해서 사용하고 있음을 알 수 있다.
def compute_cost(X, T, W, lambd):
epsilon = 1e-5
N = len(T)
K = np.size(T, 1)
cost = - (1/N) * np.ones((1,N)) @ (np.multiply(np.log(softmax(X, W) + epsilon), T)) @ np.ones((K,1))
return costcost가 손실값을 계산하는 부분이므로 여기에 L2 regularization을 더해주었다.
cost = - (1/N) * np.ones((1,N)) @ (np.multiply(np.log(softmax(X, W) + epsilon), T)) @ np.ones((K,1)) + 1 / 2 * lambd * np.sum(W ** 2)계속해서 보면
gradient descent를 사용해서 구해질 w 파라미터와 입력값인 X를 곱해서 최고의 수치를 얻은 클래스를 출력할 predict 함수가 있다.
def predict(X, W):
return np.argmax((X @ W), axis=1)이어지는 batch_gd는 mini batch를 활용한 w파라미터를 구하는 계산식이다. w = w - gd 부분이 핵심이며 gd 부분의 수식은
https://velog.io/@leeyongjoo/6-4-%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-%EA%B8%B0%EC%B4%88-%EC%84%A0%ED%98%95%EB%B6%84%EB%A5%98-2-%EC%8B%A4%EC%8A%B5
블로그를 참고하면 좋을 것 같다.
함수의 기본적인 구조는 w 값을 구해서 E(w)(comput_cost)의 값을 cost_history에 저장하고 있다.
def batch_gd(X, T, W, learning_rate, iterations, batch_size, lambd):
N = len(T)
cost_history = np.zeros((iterations,1))
shuffled_indices = np.random.permutation(N)
X_shuffled = X[shuffled_indices]
T_shuffled = T[shuffled_indices]
for i in range(iterations):
j = i % N
X_batch = X_shuffled[j:j+batch_size]
T_batch = T_shuffled[j:j+batch_size]
# batch가 epoch 경계를 넘어가는 경우, 앞 부분으로 채워줌
if X_batch.shape[0] < batch_size:
X_batch = np.vstack((X_batch, X_shuffled[:(batch_size - X_batch.shape[0])]))
T_batch = np.vstack((T_batch, T_shuffled[:(batch_size - T_batch.shape[0])]))
W = W - (learning_rate/batch_size) * (X_batch.T @ (softmax(X_batch, W) - T_batch))
cost_history[i] = compute_cost(X_batch, T_batch, W, lambd)
if i % 10000 == 0:
result = f'{i}번째 손실함수의 값은 {cost_history[i][0]}'
print(result)
return (cost_history, W)최적의 lambda 값을 구하기 위해서 수식을 만들어 보았다. lambda의 값이 임의의 값이라 최적의 lambda 값을 구하는 다양한 방식이 있다. 본인은 -10과 10 사이의 값들을 10배 단위로 lambda 값을 정리해보았고, 그중에서 -0.1과 0.1 사이의 값들에서 최고의 score가 나온다는 것을 알 수 있었다.
X = np.hstack((np.ones((np.size(X_train, 0),1)),X_train))
T = y_train
K = np.size(T, 1)
M = np.size(X, 1)
W = np.zeros((M,K))
iterations = 50000
learning_rate = 0.01
initial_cost = compute_cost(X, T, W, 0)
print("Initial Cost is: {} \n".format(initial_cost[0][0]))
lambda_score = []
lambda_list = [-0.1, -0.01, -0.001, -0.0001, -0.00001, 0, 0.00001, 0.0001, 0.001, 0.01, 0.1]
for lambd in lambda_list:
(cost_history, W_optimal) = batch_gd(X, T, W, learning_rate, iterations, 64, lambd)
y_pred = predict(X, W_optimal)
score = float(sum(y_pred == np.argmax(T, axis=1)))/ float(len(y_pred))
lambda_score.append(score)plt.figure(figsize=(10,6))
plt.plot(np.log10(lambda_list), lambda_score)
plt.show()결정경계 방정식 구하기
scikit learn에서 위에 적힌 링크를 들어가보면 결정경계 방정식을 그린 코드를 확인할 수 있다.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.linear_model import LogisticRegression
import seaborn as sns
centers = [[-5, 0], [0, 1.5], [5, -1]]
X, y = make_blobs(n_samples=1000, centers=centers, random_state=40)
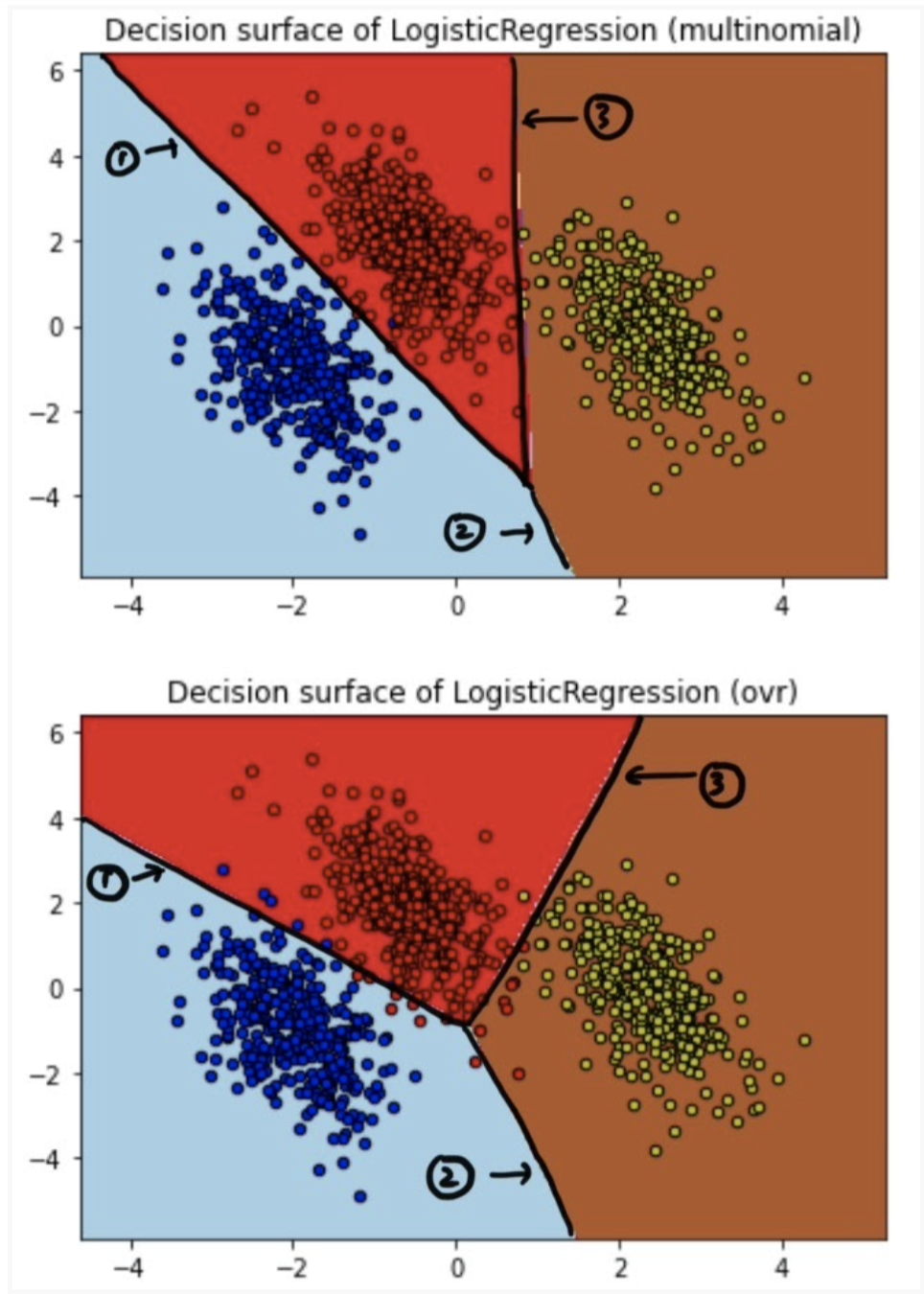
transformation = [[0.4, 0.2], [-0.4, 1.2]](multinomial)
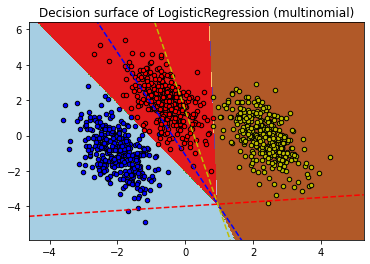
(ovr)
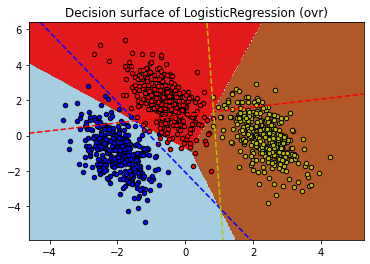
X, y값을 확인해보면 classifier가 feature가 2개인 1000개의 인풋을 3가지 클래스로 구분하는 과정임을 알 수 있다.
문제에 봉착
개인적으로 이 과제는 가설만을 세우고 멈추게 되었다.내일 당장 수업을 들어야 했기 때문에 multinomial과 ovr 방식에서 최적의 파라미터w의 값을 계수로 하는 방정식을 그리는 선에서 마무리를 했다. 추가적인 해결은 내일의 나에게 맡겨두기로...
우선 내가 세운 가설은 다음과 같다.
multinomial과 ovr 방식의 차이
1.ovr 방식에 대한 이해와 결정경계 방정식에 대한 가설.
ovr 방식은 2진 분류에 기반하는 방식이기에 로지스틱 함수를 사용한다.
z = w0 + w1x1 + w2x2라면 z값이 0이 되는 것은 두 클래스를 구분하는 직선이 만들어지는 지점이다.
z값이 0이면 시그모이드 함수의 값이 0.5가 되기 때문이다.
그림에서 살펴보면 위 그림(ovr)에서 보여지는 빨,노,파의 세가지 점선은 각각 빨간색 클래스와 나머지 클래스를 구분하는 선,
노란색 클래스와 나머지 클래스를 구분하는 선, 파란색과 나머지 클래스를 구분하는 선이다.
여기에서 결정경계를 만드는 방정식은 각 클래스를 구분하는 선들이 만드는 3개의 교점으로부터 만들어지는 것 같다.
교점 세개의 평균을 구하고 그 점으로부터 세 개의 교점을 잇는다면 결정경계 방정식이 만들어지는 것 같다.
삼각형 내부의 모든 좌표에대해서 3개의 선들과 떨어진 거리를 기준으로 중심을 찾는다고는 하는데 흠...
문제는 class가 4개 이상이 되면 ovr 방식의 계산 시간이 오래걸린다고 한다.
multinomial 방식에 대한 이해와 결정경계 방정식에 대한 가설.
ovr 방식과는 다르게 multinomial 방식은 w계수에 대한 직관적인 이해가 쉽지 않은 것 같다.
softmax 함수에서 z를 처리하는 방식이 다르기 때문이다. 그래서 multinomial을 이용해서 logistic regression을 사용한 뒤
w계수를 찾아내서 그 함수를 그려봐도 잘 이해가 되지 않는다. 따라서 결정경계 방정식에 대한 가설도 만들지 못했다...
(ovr)
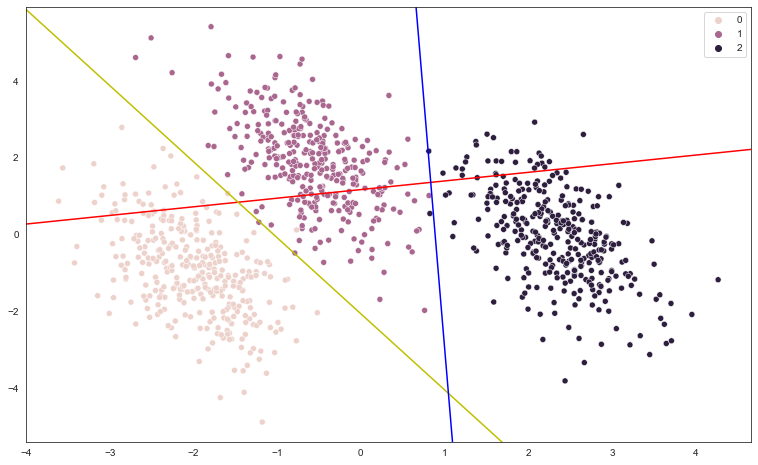
(multimonial)