심층신경망
Multi Layer Net
Multi Layer Net extended
코드 구현
class MultiLayerNetExtend:
'''
parameters
-------------------------------------
input_size : 입력크기
hidden_size_list : 각 은닉층의 뉴런 수를 담은 리스트
output_size : 출력 크기
activation : 활성화 함수 relu or sigmoid
weight_init_std : 가중치의 표준편차 (relu)he or (sigmoid)xavier
weight_decay_lambda : L2 reg lambda의 크기
use_dropout : 드롭아웃 사용 여부
dropout_ratio : 드롭아웃 비율
use_batchNorm : 배치 정규화 사용 여부
'''
def __init__(self, input_size, hidden_size_list, output_size,
activation='relu', weight_init_std='relu', weight_decay_lambda=0,
use_dropout=False, dropout_ratio=0.5, use_batchnorm=False):
self.input_size = input_size
self.output_size = output_size
self.hidden_size_list = hidden_size_list
self.hidden_layer_num = len(hidden_size_list)
self.use_dropout = use_dropout
self.weight_decay_lambda = weight_decay_lambda
self.use_batchnorm = use_batchnorm
self.params = {}
# 가중치 초기화
self.__init_weight(weight_init_std)
# 계층 생성
activation_layer = {'sigmoid' : Sigmoid, 'relu' : Relu}
# Dict에서 순서를 만들어줘야 역전파의 순서를 지킬 수 있다.
self.layers = OrderedDict()
# 만약 히든 층이 3개라면 Affine층이 4개, 활성화층 1개, softmax층이 1개이다.
# 이 과정은 instance를 만들어주는 과정이다.
# Affine - Batch - Relu - Dropout
for idx in range(1, self.hidden_layer_num+1):
self.layers['Affine' + str(idx)] = Affine(self.params['W' + str(idx)],
self.params['b' + str(idx)])
# extend, batchnorm을 사용할때 param과 layer inst.를 추가해주기
if self.use_batchnorm:
self.params['gamma' + str(idx)] = np.ones(hidden_size_list[idx-1])
self.params['beta' + str(idx)] = np.zeros(hidden_size_list[idx-1])
self.layers['BatchNorm' + str(idx)] = BatchNormalization(self.param['gamma'+str(idx)], self.params['beta'+str(idx)])
# activation은 init에서 relu or sigmoid로 고정한다.
self.layers['Activation_function' + str(idx)] = activation_layer[acvation]()
# exted, dropout을 사용할때 layer inst.를 추가해주기
if self.use_dropout:
self.layers['Dropout' + str(idx)] = Dropout(dropout_ratio)
idx = self.hidden_layer_num + 1
self.layers['Affine' + str(idx)] = Affine(self.params['W' + str(idx)],
self.params['b' + str(idx)])
self.last_layer = SoftmaxWithLoss()
def __init_weight(self, weight_init_std):
# weight_init_std : relu(he) or sigmoid(xavier)
# 이 리스트는 [784, 100, 100, ..., 10]인 리스트가 된다.
all_size_list = [self.input_size] + self.hidden_size_list + [self.output_size]
for idx in range(1, len(all_size_list)):
scale = weight_init_std
if str(weight_init_std).lower() in ('relu', 'he'):
scale = np.sqrt(2.0 / all_size_list[idx - 1])
elif str(weight_init_std).lower() in ('sigmoid', 'xavier'):
scale = np.sqrt(1.0 / all_size_list[idx - 1])
self.params['W' + str(idx)] = scale * np.random.randn(all_size_list[idx - 1], all_size_list[idx])
self.params['b' + str(idx)] = np.zeros(all_size_list[idx])
def predict(self, x, train_flg=False):
# dropout, batchnorm은 학습과 테스트 시에 달라지기 때문에
# predict를 따로 만들어주어야 한다.
for key, layer in self.layers.items():
if 'Dropout' in key or 'BatchNorm' in key:
x = layer.forward(x, train_flg)
else:
x = layer.forward(x)
return x
def loss(self, x, t, train_flg=False):
'''
손실함수를 구한다.
x : 입력 데이터
t : 정답 레이블
'''
y = self.predict(x, train_flg)
weight_decay = 0
for idx in range(1, self.hidden_layer_num + 2):
W = self.params['W' + str(idx)]
weight_decay += 0.5 * self.weight_decay_lambda * np.sum(W**2)
return self.last_layer.forward(y, t) + weight_decay
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
if t.ndim != 1:
t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x, t)
grads = {}
for idx in range(1, self.hidden_layer_num + 2):
grads['W' + str(idx)] = numerical_gradient(loss, self.params['W' + str(idx)])
grads['b' + str(idx)] = numerical_gradient(loss, self.params['b' + str(idx)])
return grads
def gradient(self, x, t):
# forward
self.loss(x, t)
# backward
dout = 1
# softmaxwithloss를 따로
dout = self.last_layer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
# Affine층에서 backward하면 dout, dw, db가 나온다.
# Relu층에서 backward하면 dout이 나온다.
dout = layer.backward(dout)
# 결과저장
# extend에서는 학습해야할 층이 6개가 더 늘었다.
grads = {}
for idx in range(1, self.hidden_layer_num + 2):
# Affine instance는 parameter에 관한 모든 정보를 담고 있다.
# L = Lcrossentropy + Lpenalty
grads['W' + str(idx)] = self.layers['Affine' + str(idx)].dW + self.weight_decay_lambda * self.layers['Affine' + str(idx)].W
grads['b' + str(idx)] = self.layers['Affine' + str(idx)].db
# idx가 4가 아니라면, 1,2,3번째 층에만 batchnorm이 있으므로
if self.use_batchnorm and idx != self.hidden_layer_num+1:
grads['gamma' + str(idx)] = self.layers['BatchNorm' + str(idx)].dgamma
grads['beta' + str(idx)] = self.layers['BatchNorm' + str(idx)].dbeta
return gradsHyperparameter
데이터 분할
우리의 최종 목표는 진짜 데이터 분포에 잘 일반화시키는 것이다. 유한한 샘플로 '본 적 없는 진짜 분포'를 만드는 것은 불가능하므로 우리는 진짜 분포의 근사 또는 불완전한 그림을 그리는 수밖에 없다.
Hyperparameter 탐색
척도
코드 구현
import sys, os
sys.path.append("./dataset")
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
import import_ipynb
from multi_layer_net_extend import MultiLayerNetExtend
# 학습을 위해서 따로 만들어준 함수들
from util import shuffle_dataset
from trainer import Trainer(x_train, y_train), (x_test, y_test) = load_mnist(normalize=True)
x_train = x_train[:500]
y_train = y_train[:500]
validation_rate = 0.20
validation_num = int(x_train.shape[0] * validation_rate)
x_train, y_train = shuffle_dataset(x_train, y_train)
x_val = x_train[:validation_num]
y_val = y_train[:validation_num]
x_train = x_train[validation_num:]
y_train = y_train[validation_num:]def __train(lr, weight_decay, epochs=50):
network = MultiLayerNetExtend(input_size=784, hidden_size_list=[100,100,100,100,100,100],
output_size=10, weight_decay_lambda=weight_decay)
trainer = Trainer(network, x_train, y_train, x_val, y_val, epochs=epochs,
mini_batch_size=100, optimizer='sgd', optimizer_param={'lr':lr}, verbose=False)
trainer.train()
return trainer.test_acc_list, trainer.train_acc_list# 하이퍼파라미터 무작위 탐색
optimization_trial = 40
results_val = {}
results_train = {}
for _ in range(optimization_trial):
# 탐색한 하이퍼 파라미터의 범위 지정
weight_decay = 10 ** np.random.uniform(-8, -4)
lr = 10 ** np.random.uniform(-6, -2)
val_acc_list, train_acc_list = __train(lr, weight_decay)
print('val acc : ' + str(val_acc_list[-1]) + ' | lr : ' + str(lr),
', weight decay : ' + str(weight_decay))
key = 'lr:' + str(lr) + ',weight decay:' + str(weight_decay)
results_val[key] = val_acc_list
results_train[key] = train_acc_listprint('Hyper-Parameter Optimization Result')
graph_draw_num = 20
col_num = 5
row_num = int(np.ceil(graph_draw_num / col_num))
i = 0
plt.figure(figsize=(10,10))
# results_val은 dict이다. key는 lr, weight_decay의 값이고
# value는 50epoch를 돌린 train에서 val_acc_list의 값들을 저장한 list이다.
# x[1]은 val_acc_list를 가리키며 여기에서 가장 마지막 값이 해당 학습의 마지막 학습률이 된다.
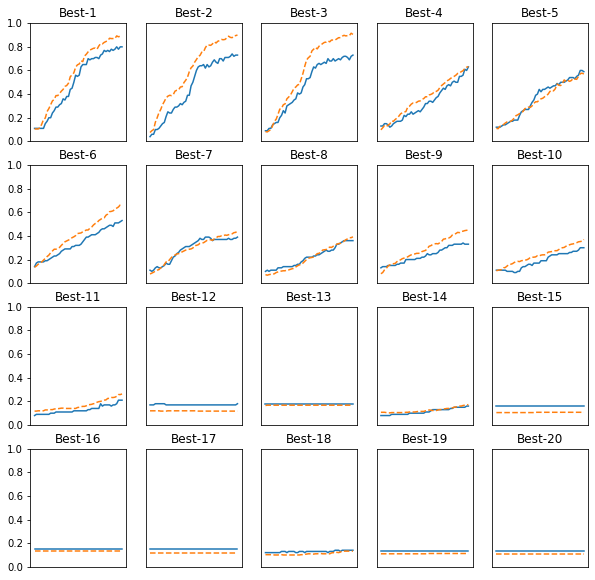
for key, val_acc_list in sorted(results_val.items(), key=lambda x: x[1][-1], reverse=True):
print('Best-' +str(i+1) + ', val acc:' + str(val_acc_list[-1]) + key)
plt.subplot(row_num, col_num, i+1)
plt.title('Best-' + str(i+1))
plt.ylim(0.0, 1.0)
if i % 5:
plt.yticks([])
plt.xticks([])
x=np.arange(len(val_acc_list))
plt.plot(x, val_acc_list)
plt.plot(x, results_train[key], '--')
i += 1
if i >= graph_draw_num:
break
plt.show()