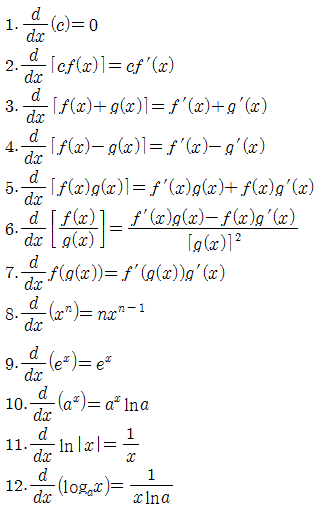[밑바닥부터 시작하는 딥러닝] #7 sigmoid, relu, softmax-with-loss층의 역전파

기본적인 미분 공식

출처 : https://dimrim.tistory.com/12

Sigmoid 함수의 역전파

현재 계수로 손실함수를 미분한 값은 upstream gradient에 현재 계수(x)로 연산의 값(y)을 미분한 local gradient를 곱한 값이다.

sigmoid계산을 연산별로 나누어서 살펴보자.

우선 나눗셈의 역전파를 보자.

exp의 역전파를 보자.

결국 sigmoid의 역전파는 x -sigmoid-> y일때 upstream gradient에 local gradient인 y(1-y)를 곱해준 값이 된다.

코드구현

class Sigmoid:
    def __init__(self):
        self.out = None
    
    def forward(self, x):
        out = sigmoid(x)
        self.out = out
        return out
    
    def backward(self, dout):
        dx = dout * (1.0 - self.out) * self.out
        
        return dx

Vanishing Gradient

층을 여러개 쌓게되면 gradient값이 소실된다는 문제가 있다.
저층에서 학습이 잘 안된다는 문제가 생긴다.

따라서 활성화 함수로 RELu를 사용하는 방법이 생긴다.

RELu 함수의 역전파

입력값이 양수이면 그대로 통과를 시키고
입력값이 음수이면 0으로 죽인다.

코드구현

class Relu:
    def __init__(self):
        self.mask = None
        
    def forward(self, x):
        self.mask = (x <= 0)
        out = x.copy()
        out[self.mask] = 0
        
        return out
    
    def backward(self, dout):
        dout[self.mask] = 0
        dx = dout
        
        return dx

Softmax-with-loss 층의 역전파

softmax와 cross entropy 함수는 각각을 합성한 함수의 도함수를 구하는 것이 더 쉽다.

계산 그래프

여러 미분계수가 합쳐지는 경우의 미분 계수는 각각의 미분계수들을 모두 더해준 값이 된다.

코드구현

t의 값이 one-hot encoding이 된 경우와 그렇지 않은 경우를 나누어서 코드를 짜야한다.

class SoftmaxwithLoss:
    def __init__(self):
        self.loss = None
        self.y = None
        self.t = None
        
    def forward(self, x, t):
        self.t = t
        self.y = softmax(x)
        self.loss = cross_entropy_error(self.y, self.t)
        
        return self.loss
    
    def backward(self, dout=1):
        batch_size = self.t.shape[0]
        if self.t.size == self.y.size: # one-hot encoded t
            dx = (self.y - self.t) / batch_size
        else:
            dx = self.y.copy()
            dx[np.arange(batch_size), self.t] -= 1
            dx = dx / batch_size
        
        return dx