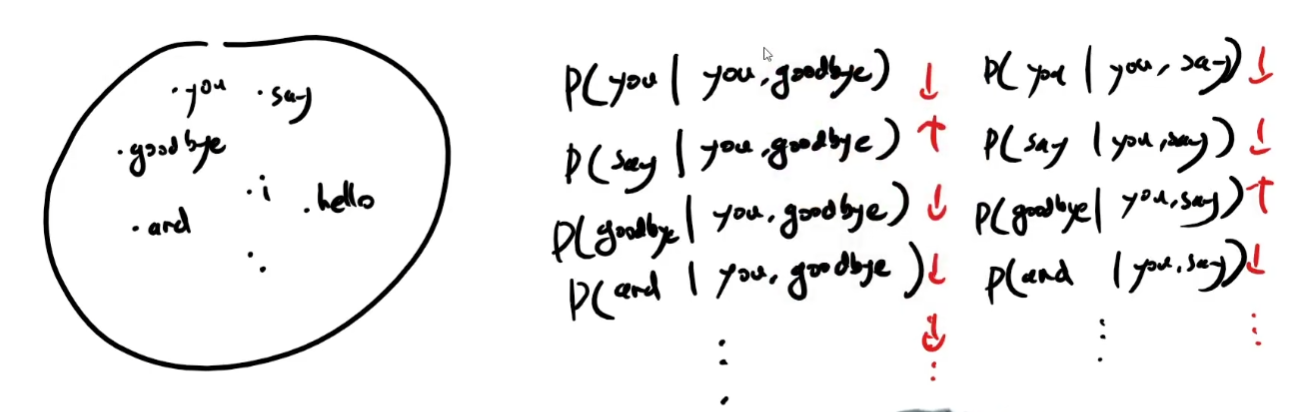[밑바닥부터 시작하는 딥러닝2] #7 순환신경망과 언어모델

지금까지는 단어를 효율적으로 벡터로 표현하는 방법을 배웠다.

언어모델

CBOW모델과 언어모델

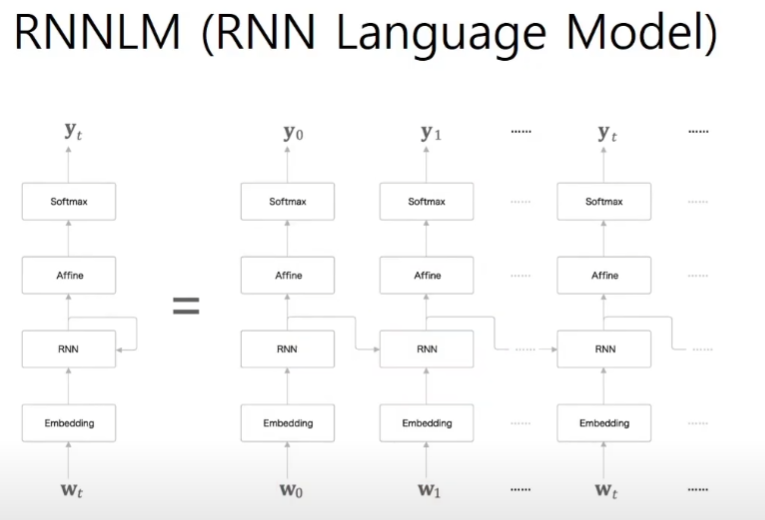
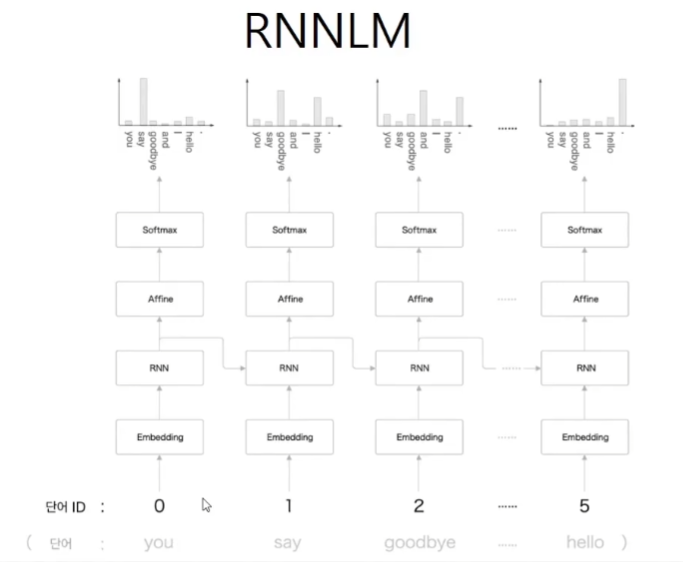
언어모델

변형 CBOW 언어모델의 문제점

통계적 언어모델의 한계점이다.
1.모든 문맥을 고려할 수 없다는 것. 설령 고려한다고 하더라도 그 길이를 충족하는 예시는 없다는 점.
2.단어의 순서를 무시한다는 점

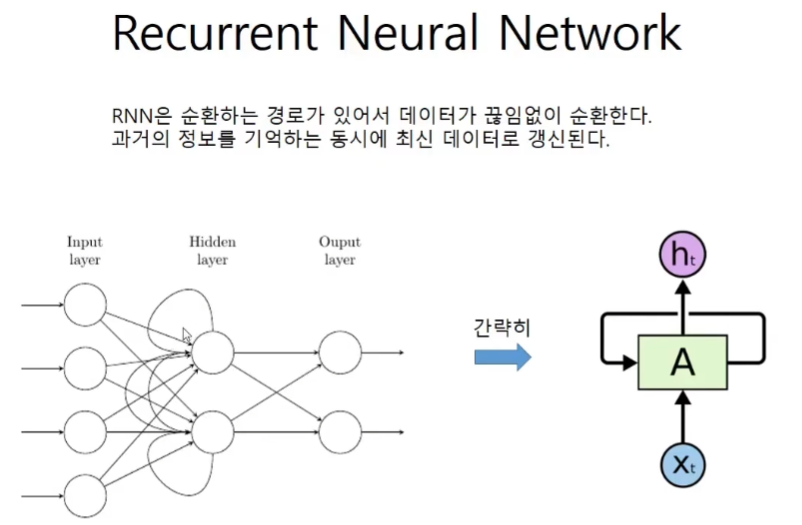
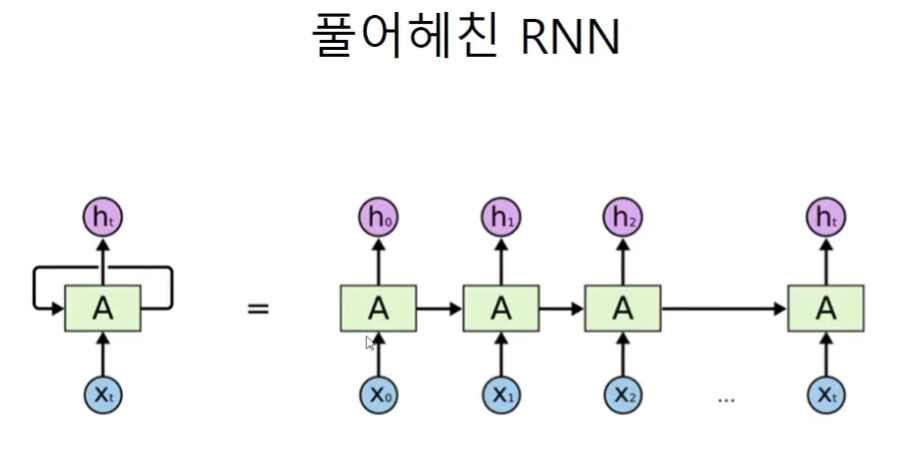
Recurrent Neural Network

역전파

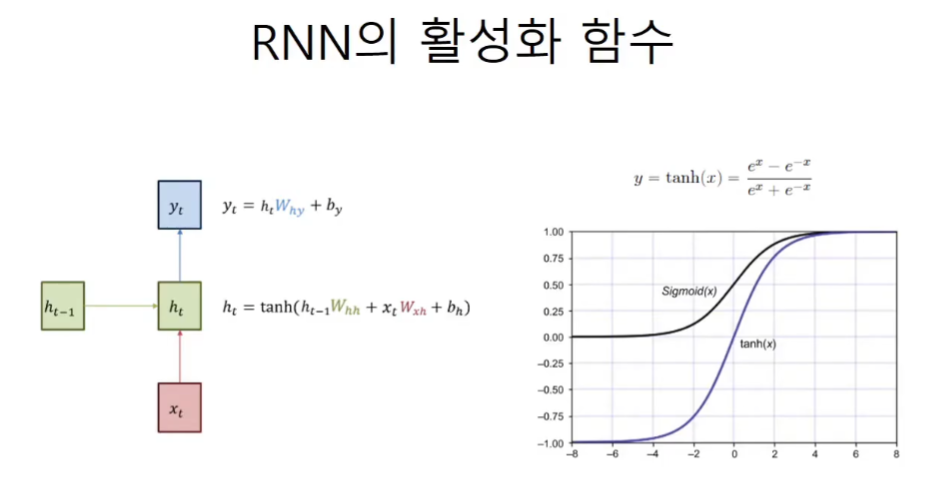
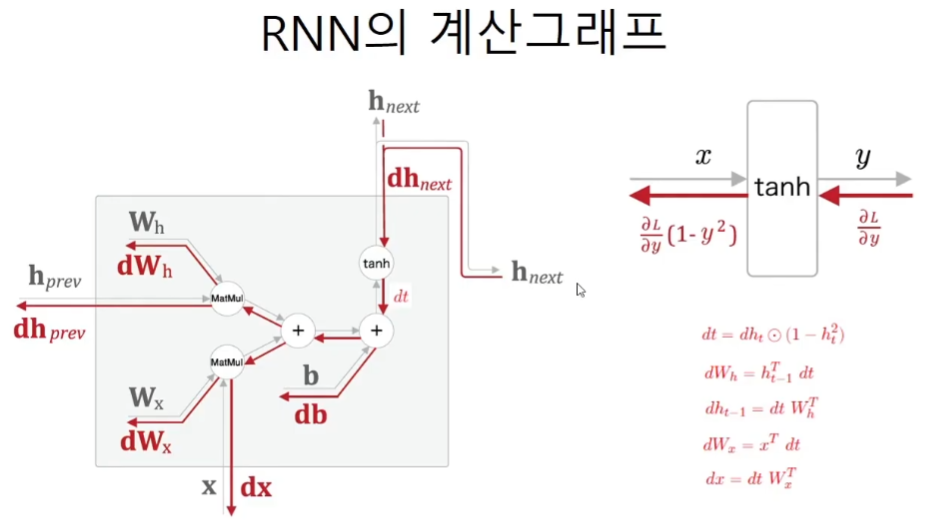
tanh

하이퍼볼릭 sin, cos, tan함수에 대해서 수학적으로 분석을 해주신다. 동영상을 참고하자. 공식이 삼각함수와 유사하기 때문에 삼각함수를 가져와서 이름을 붙여주었다.
미분 공식을 사용하여서 계산비용을 낮추는 것이 역전파의 원리이다. 마찬가지로 하이퍼볼릭 tan함수도 1-y^2이라는 간단한 도함수가 있기 때문에 사용이 가능하다.

계산그래프

코드구현

class RNN:
    def __init__(self, Wx, Wh, b):
        self.params = [Wx, Wh, b]
        self.grads = [np.zeros_like(Wx), np.zeros_like(Wh), np.zeros_like(b)]
        self.cache = none
        
    def forward(self, x, h_prev):
        Wx, Wh, b = self.params
        t = np.dot(h_prev, Wh) + np.dot(x, Wx) + b
        h_next = np.tanh(t)
        
        self.cache = (x, h_prev, h_next)
        return h_next
    
    def backward(self, dh_next):
        Wx, Wh, b = self.parmas
        x, h_prev, h_next = self.cache
        
        dt = dh_next * (1 - h_next ** 2)
        db = np.sum(dt, axis=0)
        dWh = np.dot(h_prev.T, dt)
        dh_prev = np.dot(dt, Wh.T)
        dWx = np.dot(x.T, dt)
        dx = np.dot(dt, Wx.T)
        
        self.grads[0][...] = dWx
        self.grads[1][...] = dWh
        self.grads[2][...] = db
        
        return dx, dh_prev

RNNLM