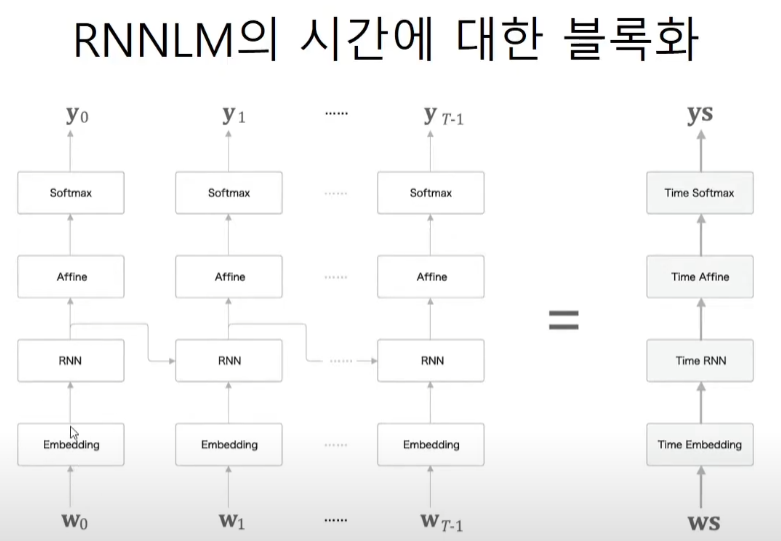
RNN through Time
우선 hidden state는 repeat node로 출력과 재사용에 나누어지기 때문에 역전파에서는 sum으로 더해줄 필요가 있다. 따라서 흘러들어오는 upstream gradient 두개를 더해준다.
그리고 affine 변환의 wh, wx의 2개, 편향벡터 1, 인풋 1, 전시점 hidden 1개까지 총 5개의 gradient가 구해지게 된다.
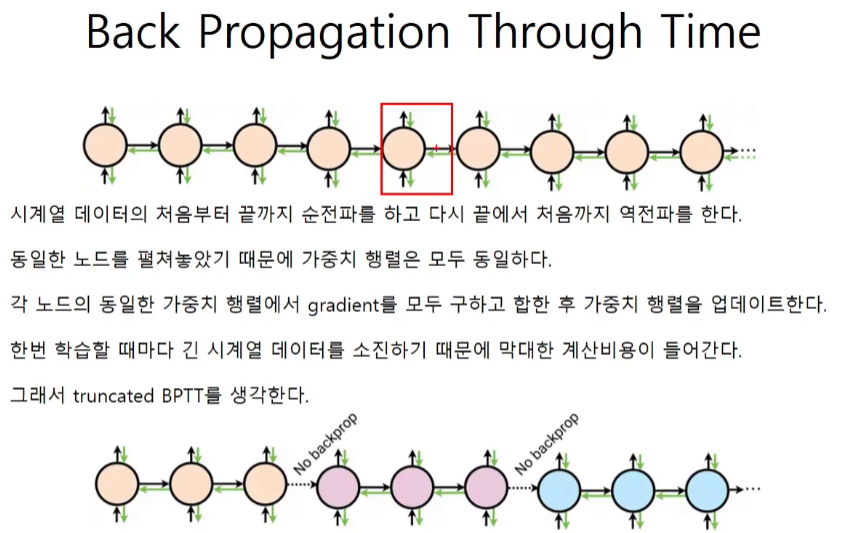
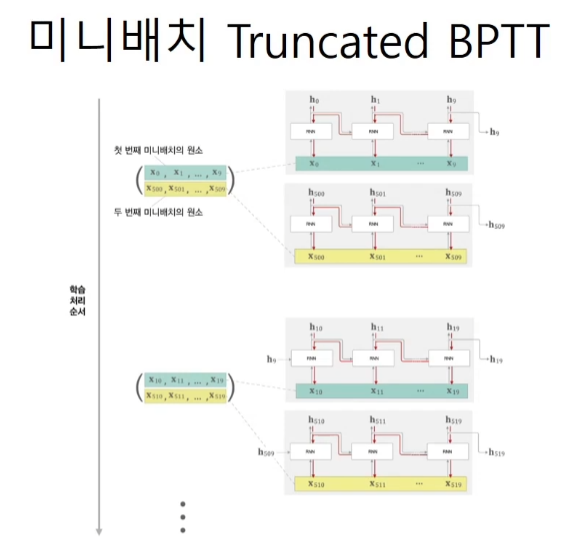
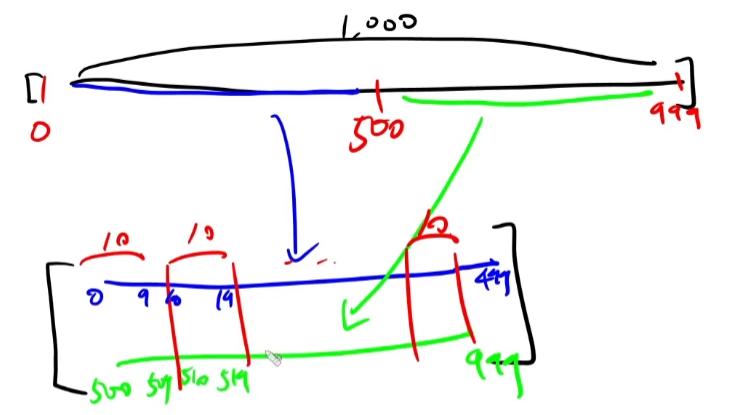
시계열 데이터를 끊어서 학습하면 RNN의 장점인 과거의 정보를 날려버린다. 그래서 truncated BPTT를 사용해서 역전파만 끊어준다.
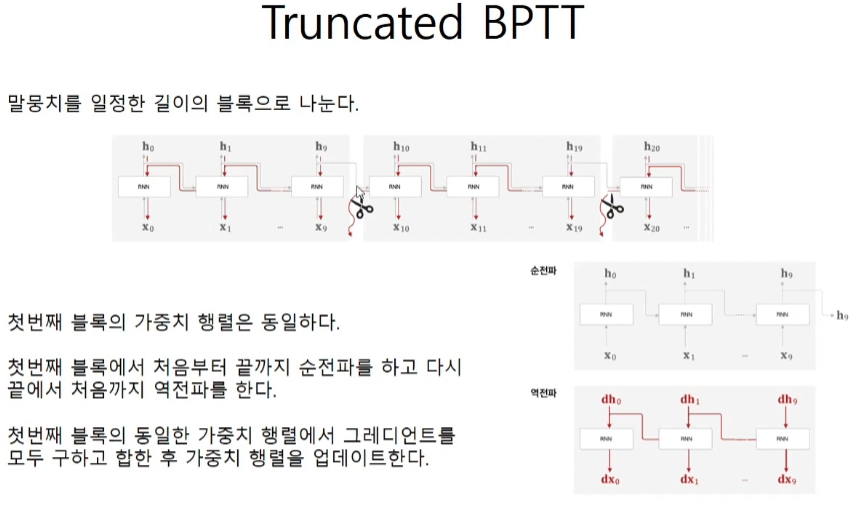
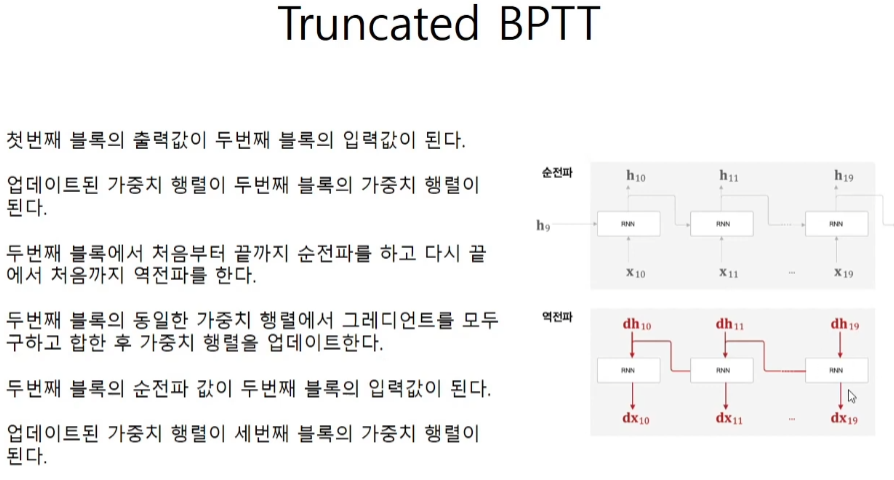
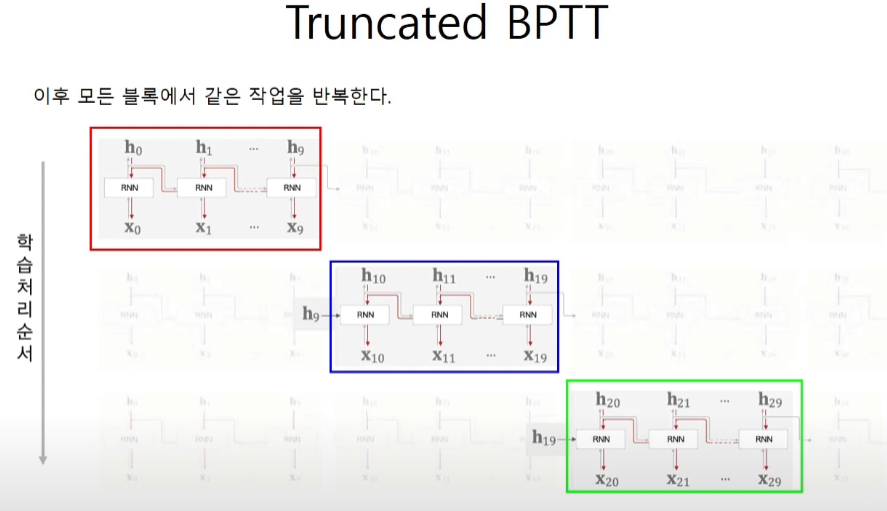
Truncated BPTT
가중치를 업데이트 하는 방식도 10개 단위로 묶은 gradient들을 한번에 더해주는 방식으로 이루어 진다.
필요한건 2가지 timeblock의 크기(10개)와 terminal의 개수(2개)이다.
time RNN 코드구현
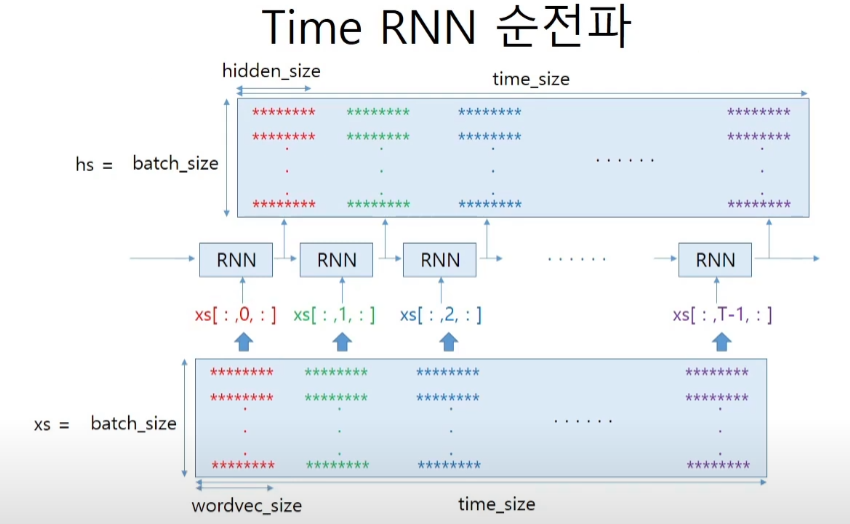
RNNLM은 corpus가 embedding층을 거친뒤 들어온다. 따라서 minibatch를 고려하면 인풋은 3차원 텐서이다.
class TimeRNN:
# stateful을 켜놓으면 다음 timeblock에 마지막 hiddenstate를 넘겨준다.
def __init__(self, Wx, Wh, b, stateful=False):
self.params = [Wx, Wh, b]
self.grads = [np.zeros_like(Wx), np.zeros_like(Wh), np.zeros_like(b)]
self.layers = None
self.h, self.dh = None, None
self.stateful = stateful
def forward(self, xs):
Wx, Wh, b = self.params
# xs는 인풋들의 모임, 3차원 텐서 인풋으로 embedding 벡터들의 집합이다.
# T는 timeblock의 size이다. 앞선 예시에선 10개였다.
# N은 사용할 truncated의 개수인거 같다.
N, T, D = xs.shape
# wx를 xs에 곱해줌으로써 H사이즈로 바꿔준다.
D, H = Wx.shape
self.layers = []
# hs는 hidden state들의 모임
hs = np.empty((N,T,H), dtype='f')
if not self.stateful or self.h is None:
self.h = np.zeros((N, H), dtype='f')
for t in range(T):
layer = RNN(*self.params)
self.h = layer.forward(xs[:, t, :], self.h)
hs[:, t, :] = self.h
self.layers.append(layer)
return hs
def backward(self, dhs):
Wx, Wh, b = self.params
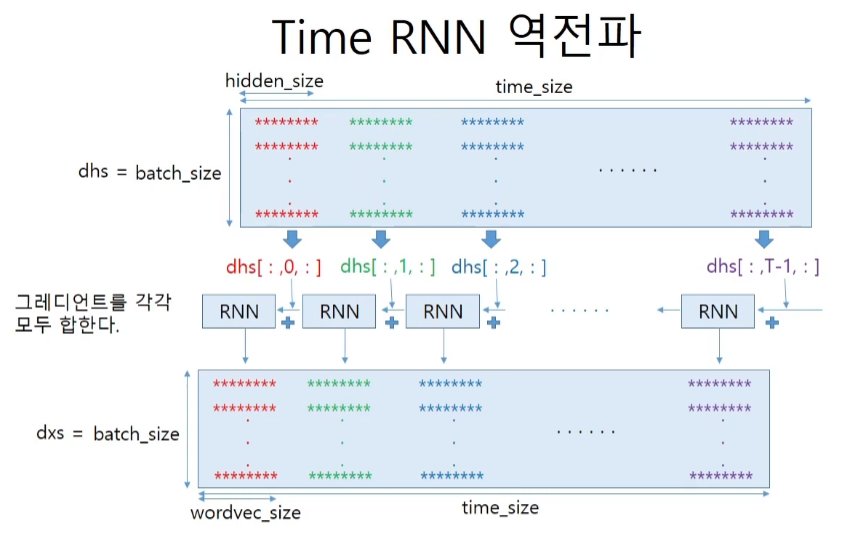
# dhs는 출력 hidden state의 upstream gradient이다.
N, T, H = dhs.shape
D, H = Wx.shape
dxs = np.empty((N,T,D), dtype='f')
# dh는 다음의 RNN에서 들어오는 hidden state의 upstream gradient이다.
dh = 0
# Wx, Wh, b로 기본 RNN에서 학습하던 가중치들이다.
grads = [0,0,0]
for t in reversed(range(T)):
layers = self.layers[t]
# h는 순전파에서 repeat되었으므로 역전파에서는 sum node로 합해준다.
dx, dh = layer.backward(dhs[:, t, :] + dh)
dxs[:, t, :] = dx
# 각 시간대별로(time block인 10개) 사용된 wx, wh, b의 값들을 모두 더해준다.
for i, grads in enumerate(layer.grads):
grads[i] += grad
for i, grad in enumerate(grads):
self.grads[i][...] = grad
self.dh = dh
return dxs
def set_state(self, h):
self.h =h
def reset_state(self):
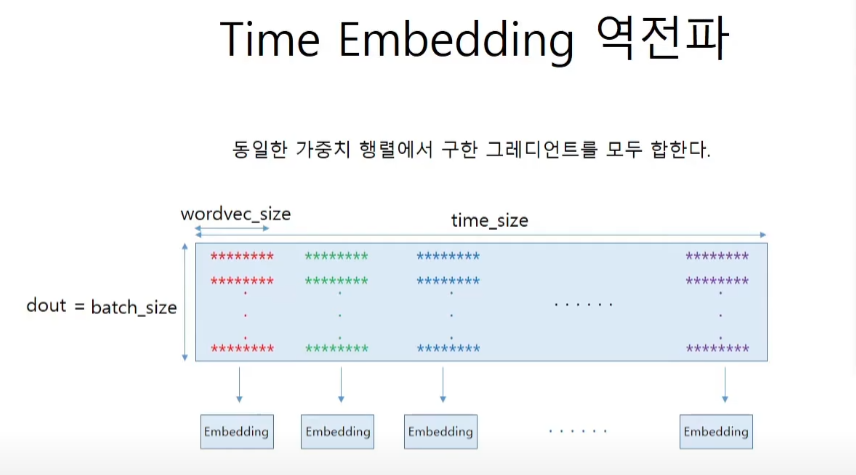
self.h = Nonetime Embedding 코드구현
class TimeEmbedding:
def __init__(self, W):
self.params = [W]
self.grads = [np.zeros_like(W)]
self.layers = None
self.W = W
def forward(self, xs):
# N = batch_size, T = time_size
N, T = xs.shape
# vocabulary_size : 단어의 개수, dense_size : 임베딩 차원
V, D = self.W.shape
out = np.empty((N,T,D), dtype='f')
self.layers = []
for t in range(T):
layer = Embedding(self.W)
# 아무렇게나 만든 out에 제대로된 임베딩 벡터를 넣어준다.
out[:,t,:] = layer.forward(xs[:,t])
self.layers.append(layer)
return out
def backward(self, dout):
N, T, D = dout.shape
grad = 0
for t in range(T):
layer = self.layers[t]
layer.backward(dout[:, t, :])
# grads = [W]이므로 [0]로 벗겨준다.
grad += layer.grads[0]
self.grads[0][...] = grad
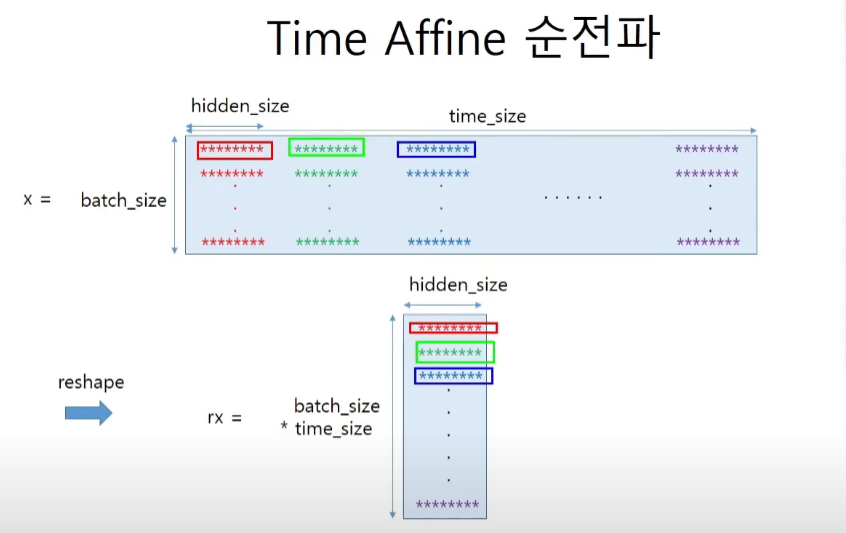
return Nonetime Affine 코드 구현
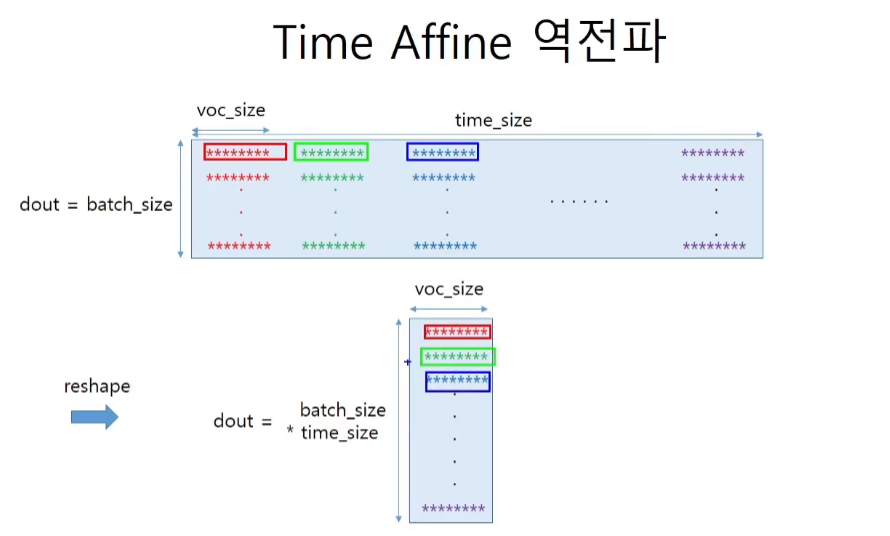
affine층의 역할을 생각해보자. softmax에 넣어주기 전에 vocabulary 사이즈 만큼의 벡터를 표현하는 행렬이 나와줘야한다. 즉 hidden_size에 가중치W를 곱해서 voc_size를 만들어서(one-hot인가?) score를 부여하는 것이 이 층의 역할이다.
class TimeAffine:
def __init__(self, W, b):
self.params = [W, b]
self.grads = [np.zeros_like(W), np.zeros_like(b)]
self.x = None
def forward(self, x):
N, T, D = x.shape
w, b = self.params
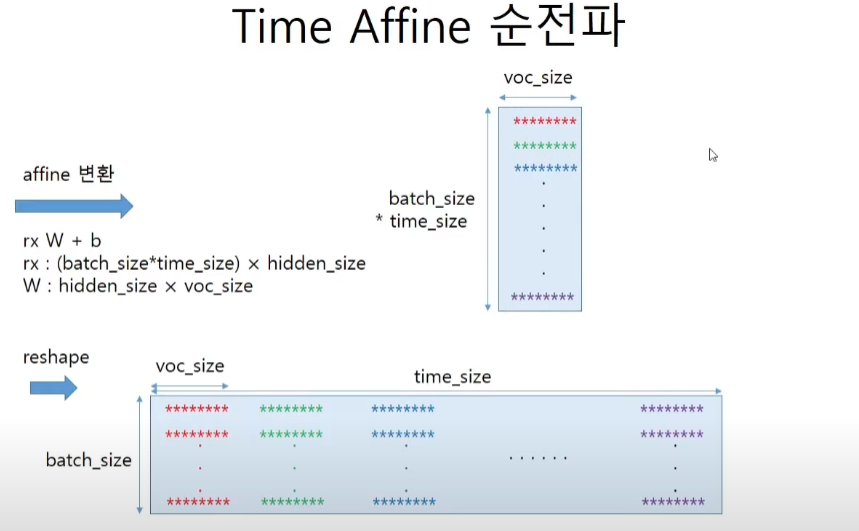
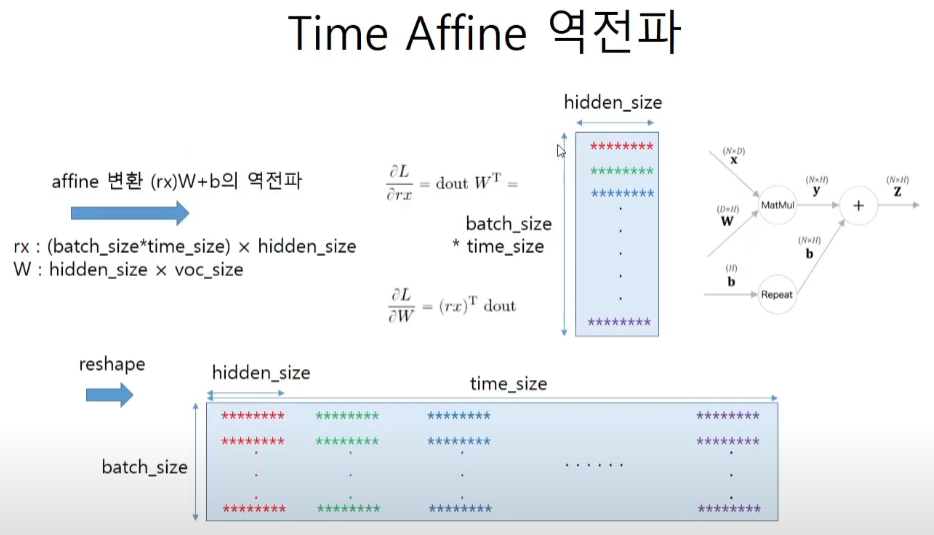
# 이미지 참조
# 임베딩 벡터를 하나의 열로 만들어주면 단 한번의 곱셈으로 모든걸 표현할 수 있다.
rx = x.reshape(N*T, -1)
out = np.dout(rx, W) + b
self.x = x
return out.reshape(N, T, -1)
def backward(self, dout):
x = self.x
N, T, D = x.shape
W, b = self.params
dout = dout.reshape(N*T, -1)
rx = x.reshape(X*T, -1)
db = np.sum(dout, axis=0)
dW = np.dot(rx.T, dout)
dx = np.dot(dout, W.T)
dx = dx.reshape(*x.shape)
self.grads[0][...] = dW
self.grads[1][...] = db
return dxtime Softmax 코드구현
class TimeSoftmaxWithLoss:
def __init__(self):
self.params, self.grads = [], []
self.cache = None
self.ignore_label = -1
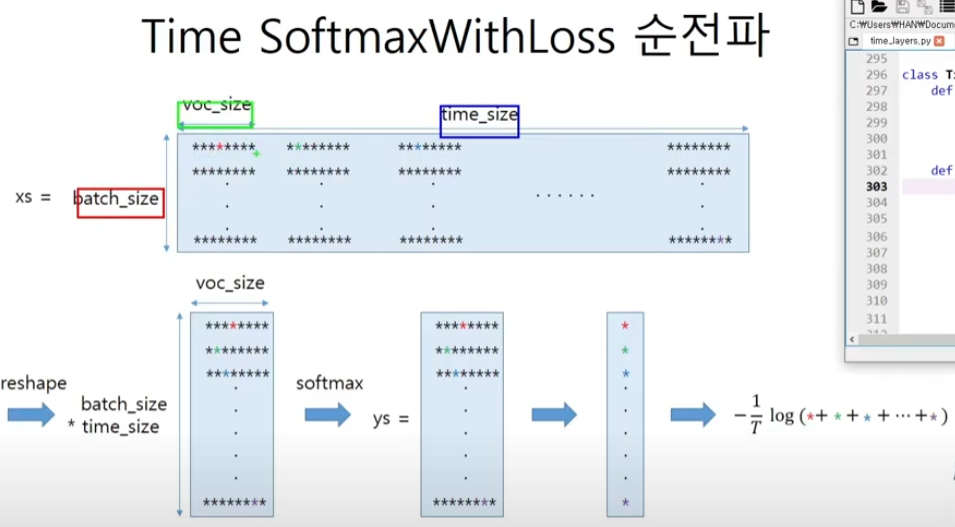
def forward(self, xs, ts):
N, T, V = xs.shape
# 정답 레이블이 원핫 벡터인 경우
# batch x time_size x vector or single number
if ts.ndim == 3:
ts = ts.argmax(axis=2)
# True or False
mask = (ts != self.ignore_label)
# 배치용과 시계열용을 정리(reshape)
xs = xs.reshape(N*T, V)
# flatten
ts = ts.reshape(N*T)
mask = mask.reshape(N*T)
ys = softmax(xs)
# label에 해당하는 xs를 뽑아낸다. cross entropy를 구하는 과정이다.
ls = np.log(ys[np.arange(N*T), ts])
# ignore_label에 해당하는 데이터는 손실을 0으로 설정
ls *= mask
loss = -np.sum(ls)
loss /= mask.sum()
self.cache = (ts, ys, mask, (N, T, V))
return loss
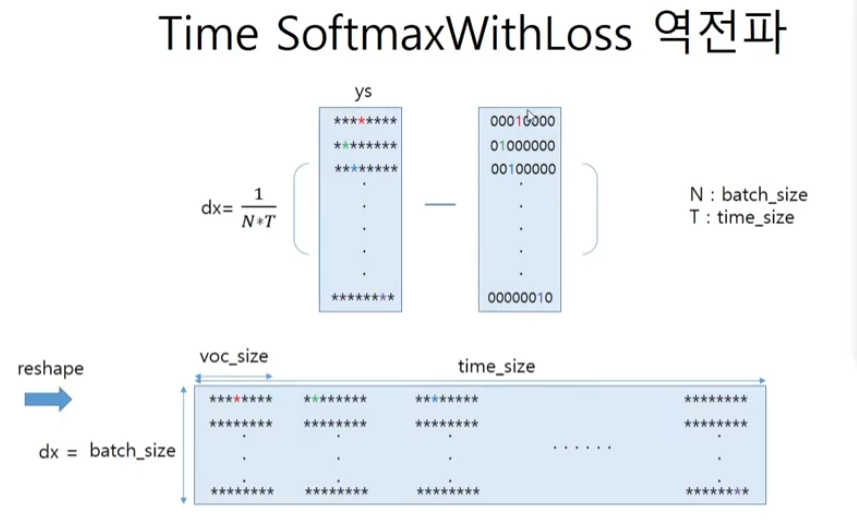
def backward(self, dout=1):
ts, ys, mask, (N,T,V) = self.cache
dx = ys
dx[np.arange(N*T), ts] -= 1
dx *= dout
dx /= mask.sum()
# ignore_label에 해당하는 데이터는 기울기를 0으로 설정
dx *= mask[:, np.newaxis]
dx = dx.reshape((N, T, V))
return dx최종 RNNLM 코드 구현
class SimpleRnnlm:
def __init__(self, vocab_size, wordvec_size, hidden_size):
V, D, H = vocab_size, wordvec_size, hidden_size
rn = np.random.randn
# 가중치 초기화 He, javier 초기값
embed_W = (rn(V, D) / 100).astype('f')
rnn_Wx = (rn(D, H) / np.sqrt(D)).astype('f')
rnn_Wh = (rn(H, H) / np.sqrt(H)).astype('f')
rnn_b = np.zeros(H).astype('f')
affine_W = (rn(H, V) / np.sqrt(H)).astype('f')
affine_b = np.zeros(V).astype('f')
# 계층 생성
self.layers = [
TimeEmbedding(embed_W),
TimeRNN(rnn_Wx, rnn_Wh, rnn_b, stateful=True),
TimeAffine(affine_W, affine_b)
]
self.loss_layer = TimeSoftmaxWithLoss()
self.rnn_layer = self.layers[1]
# 모든 가중치와 기울기를 리스트에 모은다.
self.params, self.grads = [], []
for layer in self.layers:
self.params += layer.params
self.grads += layer.grads
# 집어 넣는 단어xs의 다음 단어가 정답ts이다.
def forward(self, xs, ts):
for layer in self.layers:
xs = layer.forward(xs)
loss = self.loss_layer.forward(xs, ts)
return loss
def backward(self, dout=1):
dout = self.loss_layer.backward(dout)
for layer in reversed(self.layers):
dout = layer.backward(dout)
return dout
def reset_state(self):
self.rnn_layer.reset_state()