선형대수와 해석기하의 기초
https://datascienceschool.net/intro.html 참고
벡터의 기하학적 의미
N차원 벡터 a는 N차원의 공간에서
-
벡터 a의 값으로 표시되는 점(point) 또는
-
원점과 벡터 a의 값으로 표시되는 점을 연결한 화살표(arrow)
라고 생각할 수 있다.
벡터의 길이
벡터 a의 길이는 놈(norm) ∥a∥으로 정의한다. norm에는 여러가지가 있다. 다음은 유클리드 norm이다.
단위벡터
길이가 1인 벡터를 단위벡터(unit vector)라고 한다. 예를 들어 다음과 같은 벡터들은 모두 단위벡터다.
임의의 벡터 x에 대해서 다음 벡터는 벡터 x와 같은 방향을 가리키는 단위벡터가 된다.
x / ∥x∥
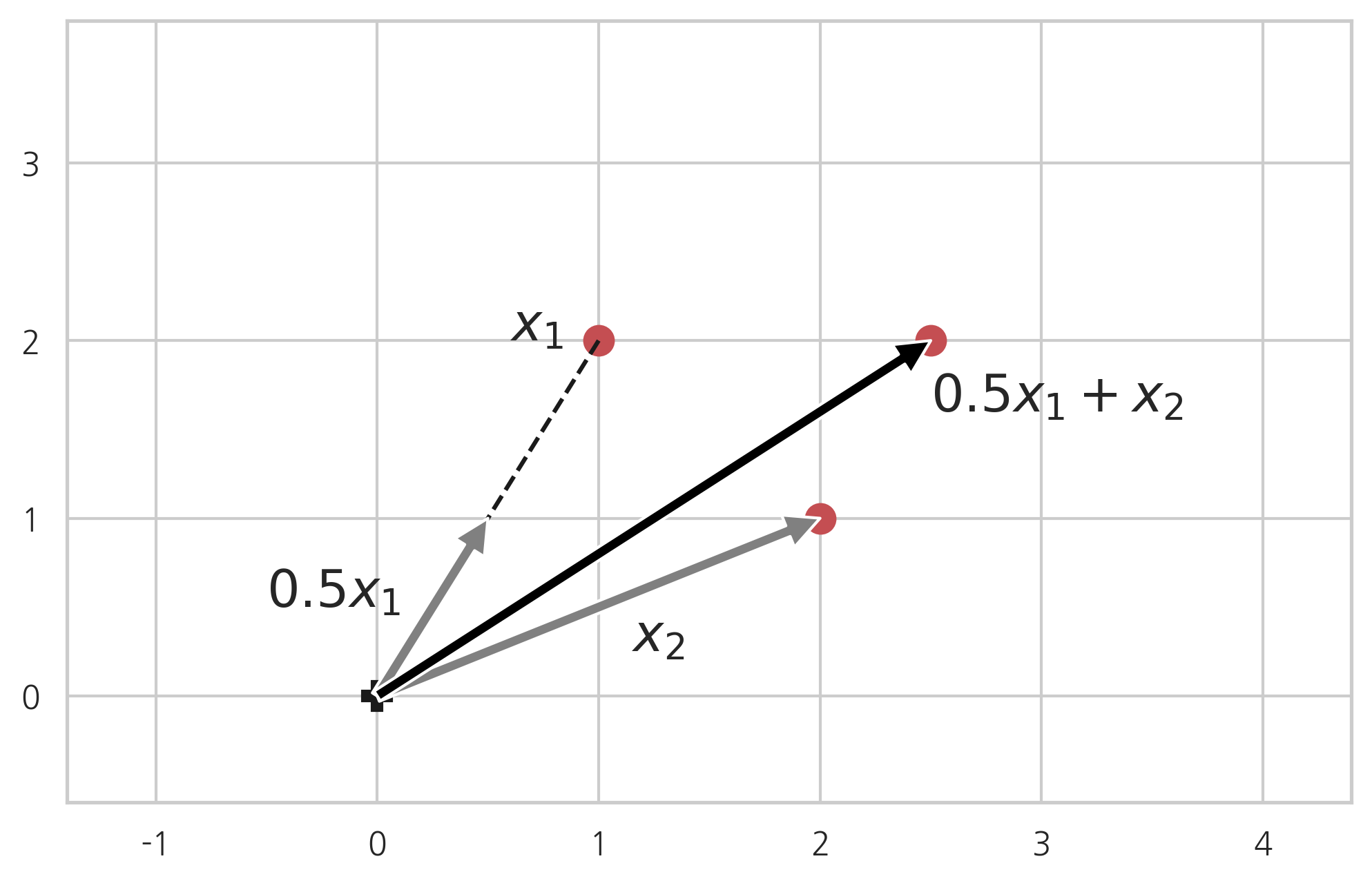
벡터의 선형조합
벡터의 스칼라곱과 두 벡터의 합에 대해서는 본문에서 다루지 않았다. 여러 개의 벡터를 스칼라곱을 한 후 더한 것을 선형조합(linear combination)이라고 한다.
c1x1+c2x2+⋯+cNxN
유클리드 거리
두 벡터가 가리키는 점 사이의 거리를 유클리드 거리(Euclidean distance)라고 한다. 두 벡터의 유클리드 거리는 벡터의 차의 길이로 구할 수 있다.
벡터의 놈의 정의와 벡터의 차의 정의에서 유클리드 거리는 다음처럼 구한다.
벡터의 내적과 삼각함수
두 벡터의 내적은 다음처럼 벡터의 길이 ∥a∥, ∥b∥ 와 두 벡터 사이의 각도 θ의 코사인 함수값으로 계산할 수도 있다.
aTb=∥a∥∥b∥cosθ
직교(orthogonal)와 정규직교(orthonormal), 그리고 직교행렬(orthogonal matrix)
orthogonal: v1·v2 = 0
orthonormal: v1·v2 = 0 & ∥v1∥ = 1, ∥v2∥ = 1
직교행렬(orthogonal matrix)의 수학적 정의는 자신의 전치행렬(transpose)를 역행렬로 갖는 정방행렬이다.
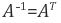
직교행렬의 열벡터들은 서로 orthonormal(정규직교)한 성질을 가지고 있다. 즉, 직교 행렬를 구성하는 열벡터들을 v1, v2, ..., vn이라 했을 때 이들은 모두 단위벡터(unit vector)이면서 또한 서로 서로 수직인 성질을 갖는다.
