문제

N개의 수가 주어졌을 때, XOR한 값이 가장 큰 두 수를 찾는 프로그램을 작성하시오.

즉, A1, A2, ..., AN 중에서 i ≠ j이면서 Ai XOR Aj 가 가장 큰 것을 찾아야 한다.

입력

첫째 줄에 N (2 ≤ N ≤ 100,000)이 주어진다.

둘째 줄에는 N개의 수가 주어진다. 입력으로 주어지는 수는 1,000,000,000보다 작거나 같은 음이 아닌 정수이다.

출력

첫째 줄에 XOR한 값이 가장 큰 두 수의 XOR한 결과를 출력한다.

https://www.acmicpc.net/problem/13505

풀이

먼저 정수의 XOR를 계산하자하면 먼저 2진수간의 XOR연산이 어떻게 이루어지는지 생각해볼 수 있다.
결국 서로다른 비트일경우 XOR값이 1이되므로,
하나의 정수를 변환한 2진수와
모든 자릿수의 비트를 반전시키면 그 결과는 최댓값이 되는것이다.
여기서

• 2진수의 맨끝자리의 비트가 반전되면 결과값이 더 크다.
• 10억까지의 수는 30개의 비트로 표현가능하다.

이 두가지를 생각해보면 2진수를 구현할때 무조건 30비트를 갖게하며, 역전시켜서 저장하면 되야함을 알 수 있다.
또 각 자리의 비트를 탐색해야하므로 트리구조를 이용하는 Trie자료구조를 만들면 쉽게 계산가능하다.
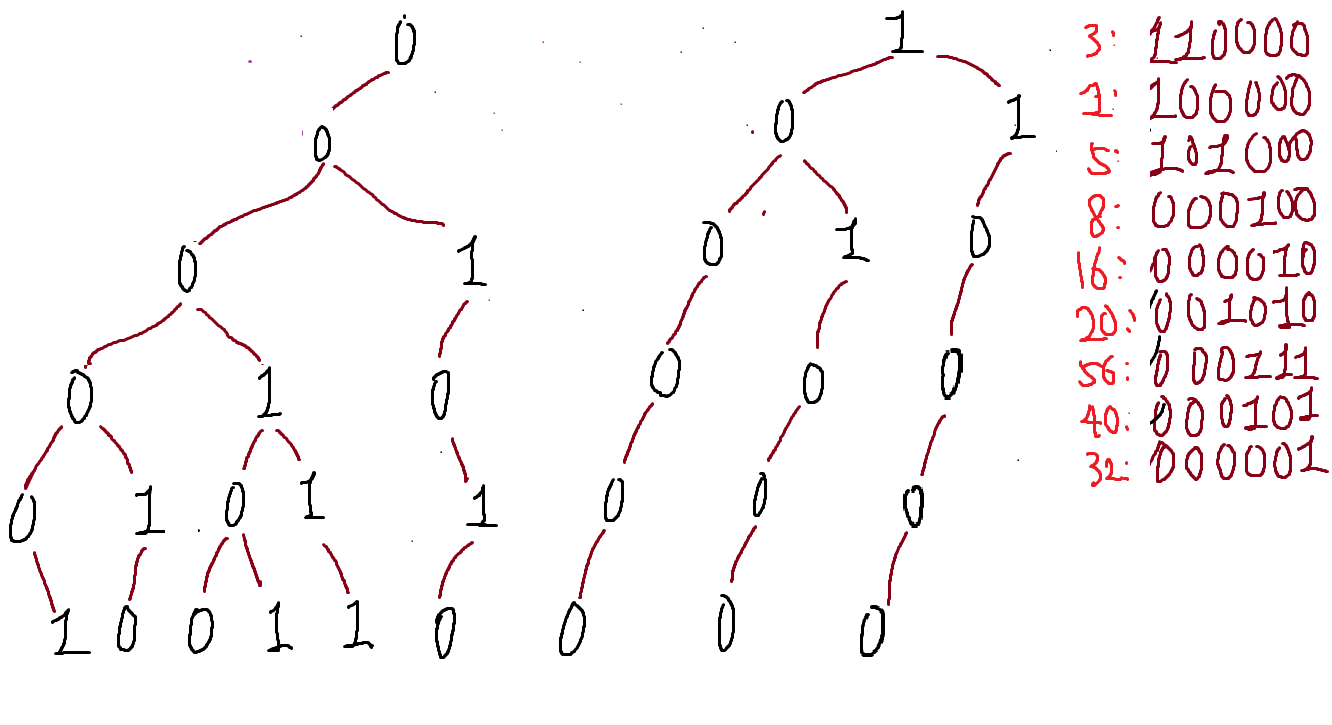
아래의 그림을 보자.

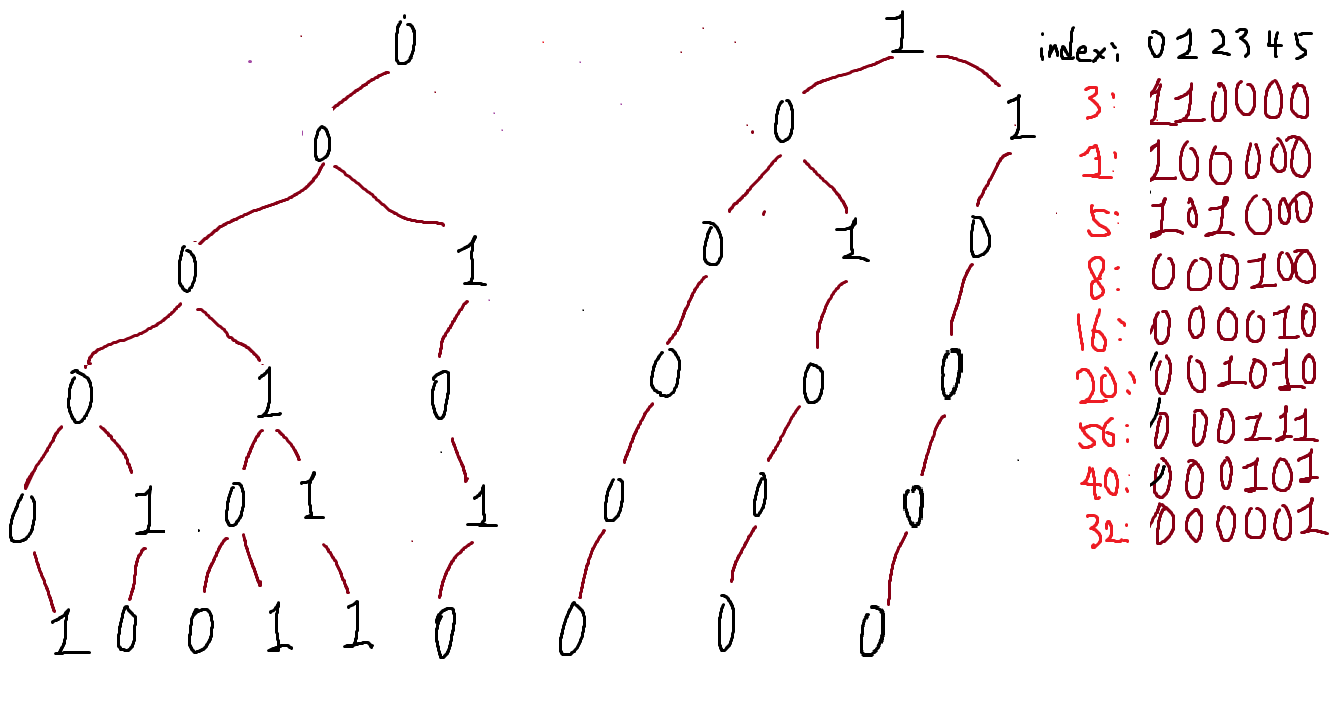
오른쪽에 빨간색으로 적힌 정수를 2진수로 변환한다음 역순으로 적은것이 갈색 2진수고,
그것을 0번째인덱스부터 차례대로 그려내려가면
왼쪽의 트리가 된다. 이것이 저장될 Trie구조이다
모든 2진수를 30비트로 표현할것이므로, 빈자리에는 0이 계속채워져서
이 Trie구조는 완전이진트리 형태를 띄게된다.

자세한 설명은 코드에 주석으로 남겨 놓았다.

#define _CRT_SECURE_NO_WARNINGS 
#include <bits/stdc++.h>
#define mp std::make_pair 
#define mt std::make_tuple
#define dq std::deque
#define pq std::priority_queue
#define sw std::swap
#define ts(x) std::to_string(x)
#define tc() c_str()
#define sc(x, ...) scanf(x, ##__VA_ARGS__) 
#define pr(x, ...) printf(x, ##__VA_ARGS__) 
#define ins(x) insert(x)
#define pb(x) push_back(x)
#define pf(x) push_front(x)
#define PB() pop_back()
#define PF() pop_front()
#define ph(x) push(x)
#define TT() top()
#define PP() pop()
#define BB() back()
#define FF() front()
#define cls() clear()
#define emp() empty()
#define len(x) x.length()
#define sz(x) ((int)x.size()) //컨테이너에서 사용
#define ms(a) memset(a, 0, sizeof(a)) //0으로 초기화
#define rep(i, n) for(int i = 0; i < n ; i++)
#define rrep(i, r, n) for(int i = r; i < n ; i++)
#define rrrep(i, r, n) for(ll i = r; i < n ; i++)
#define _rrep(i, r, n) for(int i = r; i >= n; i--)
#define _rrrep(i, r, n) for(ll i = r; i >= n; i--)
#define each(x, a) for (auto& x: a)
#define all(x) x.begin(),x.end() //STL에서 전체 처리할때 사용
#define range(x, r, n) x.begin() + r, x.begin() + n //STL에서 구간설정
#define ct continue
#define br break
#define rt return
#define _TYF typedef //코드줄이기
#define _UG using
#define _TCE template <class T> inline
//#define MAX 
const int IMAX = INT32_MAX; const int IMIN = INT32_MIN;
const long long LMAX = LLONG_MAX; const long long LMIN = LLONG_MIN;
const long double PI = 3.141592653589793238462643383279502884197;
_UG std::vector; _UG std::stack; _UG std::queue; _UG std::tuple; _UG std::set; _UG std::list; _UG std::bitset; _UG std::string; _UG std::pair; _UG std::greater;
_UG std::tie; _UG std::sort; _UG std::max_element; _UG std::min_element; _UG std::fill; _UG std::stoi; _UG std::stod; _UG std::stof; _UG std::stol; _UG std::stold; _UG std::stoll; _UG std::stoul; _UG std::stoull; _UG std::to_string;
//_UG std::max; //_UG std::min; //_UG std::map;
_TYF long long ll; _TYF unsigned long long ull;
_TYF pair<int, int> pii; _TYF pair<double, int> pdi; _TYF pair<int, double> pid; _TYF pair<double, double> pdd; _TYF pair<int, ll> pil;
_TYF pair<ll, int> pli; _TYF pair<ll, ll> pll; _TYF pair<ull, ull> pullull; _TYF pair<int, char> pic; _TYF pair<char, int> pci;
_TYF pair<char, char> pcc; _TYF pair<long, char> plc; _TYF pair<char, long> pcl; _TYF pair<ll, char> pllc; _TYF pair<char, ll> pcll;
_TYF pair<ull, char> pullc; _TYF pair<char, ull> pcull; _TYF pair<int, string> pis; _TYF pair<string, int> psi; _TYF pair<long, string> pls;
_TYF pair<string, long> psl; _TYF pair<ll, string> plls; _TYF pair<string, ll> psll; _TYF pair<ull, string> pulls;
_TYF pair<string, ull> psull; _TYF pair<string, string> pss;
_TYF tuple<int, int, int> tiii; _TYF tuple<int, int, int, int> tiiii;
_TYF tuple<ll, ll, ll> tlll; _TYF tuple<ll, ll, ll, ll> tllll;
_TYF vector<string> vs; _TYF queue<string> qs; _TYF stack<string> ss; _TYF dq<string> dqs; _TYF pq<string> pqs; _TYF dq<string> dqs;
_TYF vector<char> vc; _TYF queue<char> qc; _TYF stack<char> sc; _TYF dq<char> dqc; _TYF pq<char> pqc; _TYF dq<char> dqc;
_TYF vector<int> vi; _TYF queue<int> qi; _TYF stack<int> si; _TYF dq<int> dqi; _TYF pq<int> pqi; _TYF dq<int> dqi;
_TYF vector<pii> vii; _TYF queue<pii> qii; _TYF stack<pii> sii; _TYF dq<pii> dqii; _TYF pq<pii> pqii; _TYF dq<pii> dqii;
_TYF vector<tiii> viii; _TYF queue<tiii> qiii; _TYF stack<tiii> siii; _TYF dq<tiii> dqiii; _TYF pq<tiii> pqiii; _TYF dq<tiii> dqiii;
_TYF vector<tiiii> viiii; _TYF queue<tiiii> qiiii; _TYF stack<tiiii> siiii; _TYF dq<tiiii> dqiiii; _TYF pq<tiiii> pqiiii; _TYF dq<tiiii> dqiiii;
_TYF vector<pll> vll; _TYF queue<pll> qll; _TYF stack<ll> sll; _TYF dq<pll> dqll; _TYF pq<pll> pqll; _TYF dq<pll> dqll;
_TYF vector<tlll> vlll; _TYF queue<tlll> qlll; _TYF stack<tlll> slll; _TYF dq<tlll> dqlll; _TYF pq<tlll> pqlll; _TYF dq<tlll> dqlll;
_TYF vector<tllll> vllll; _TYF queue<tllll> qllll; _TYF stack<tllll> sllll; _TYF dq<tllll> dqllll; _TYF pq<tllll> pqllll; _TYF dq<tllll> dqllll;
_TCE T sq(T num) { rt num* num; }//제곱함수
_TCE T GCD(T num1, T num2) { if (num2 == 0) rt num1; rt GCD(num2, num1 % num2); }
_TCE T LCM(T num1, T num2) { if (num1 == 0 || num2 == 0) rt num1 + num2; rt num1* (num2 / GCD(num1, num2)); }
//STL 전용 초기화 함수들 ( ms~~ )
_TCE void msq(T& a) { while (!a.empty()) a.PP(); }//queue clear
_TCE void msv(T& a) { a.cls(); }//vector clear
_TCE void msdq(T& a) { a.cls(); }//deque clear
_TCE void msm(T& a) { a.cls(); }//map clear
_TCE void mss(T& a) { while (!a.empty()) a.PP(); }//stack, set clear
_TCE void mspq(T& a) { while (!a.empty()) a.PP(); }//priority_queue clear
//pii operator - (pii a, pii b) { rt pii(a.first - b.first, a.second - b.second); }
//bool operator <= (pii a, pii b) { rt a.first <= b.first && a.second <= b.second; } 
//bool operator >= (pii a, pii b) { rt a.first >= b.first && a.second >= b.second; } 
//bool operator < (pii a, pii b) { if (a == b) return false; rt a <= b; } 
//bool operator > (pii a, pii b) { if (a == b) return false; rt a >= b; }

int N;
vi number; //입력받은 정수들
int binary[31]; //10억까지의정수는 30개의 비트로 저장가능. 31번째비트는 맨끝을 나타낼것

struct BinaryTrie {
private:
	BinaryTrie* node[2];

public:
	BinaryTrie() : node() {}

	//2진수인 binaryArr배열을 Trie구조로 만듬
	void insert(int *binary) {
		if (*binary == -1) rt;

		if (node[*binary] == nullptr)
			node[*binary] = new BinaryTrie();

		node[*binary]->insert(binary + 1);
	}

	//Trie구조내의 하나의 2진수를 선택해
	//해당 2진수와 XOR결과가 최댓값이 되는 다른 2진수를 찾는 함수
	//선택한 2진수의 각 비트마다 반전시킨비트가 있으면 찾고 없으면 같은비트를 탐색
	//즉 0, 1비트는 모두 존재하니 둘중 최적의 비트(XOR결과가 1되는)를 따라감
	void search(int *binary) {
		if (*binary == -1) rt;

		int bit = *binary; //현재 비트

		//XOR값이 크려면 2진수 맨끝비트부터 탐색할때 XOR값이 최대가 될려면
		//각자리 비트마다 반전시킨 비트를 찾으면됨 (서로다른비트는 XOR결과 1, 같으면 0)
		//우리는 2진수를 역순으로 넣었으니 binary의 0번인덱스부터 탐색하는게 맨끝비트부터 탐색하는것
		//가능한 XOR가 최대가되는 노드를 선택해 따라가면
		//Trie구조로 편입된 2진수중 하나를 택하게됨.
	
		//1순위 : 반전시킨 비트가 있으면 따라감 (XOR 결과 1, 최댓값임)
		if (node[bit ^ 1] != nullptr) { 
			*binary = bit ^ (bit ^ 1); //원래비트와 반전시킨 비트가 있으니 XOR한 결과는 1
			node[bit ^ 1]->search(binary + 1); //찾은 비트의 노드를 따라가 탐색
			
		}//2순위 : 반전시킨 비트가 없으면 남은 비트를 따라감(XOR결과 0)
		else { 
			*binary = bit ^ bit; //원래비트와 같은비트만 있으니 XOR한 결과는 0
			 node[bit]->search(binary + 1); //찾은 비트의 노드로..
		}
	}
};

//프로그램 메인 로직
void func() {
	BinaryTrie bt;
	sc("%d", &N);
	binary[30] = -1;

	rep(_, N) { //정수를 입력받아 2진수로 Trie구조로 편입
		int n;
		sc("%d", &n);
		number.pb(n);
		_rrep(i, 29, 0) { //2진수로 변환하되 역순으로 Trie구조에 편입
			n & 1 ? binary[i] = 1 : binary[i] = 0;
			n >>= 1;
		}
		//입력받은 정수를 2진수로바꾸어 Trie구조에 편입
		bt.insert(binary);
	}

	int maxXOR = 0; //XOR최댓값
	rep(k, sz(number)) {
		int n = number[k];
		//정수를 2진수로 변환해서 binary에 저장
		_rrep(i, 29, 0) {
			n & 1 ? binary[i] = 1 : binary[i] = 0;
			n >>= 1;
		}
		//binary와 XOR결과가 최대가되는 2진수를 찾아서 다시 binary에 덮어씌움
		bt.search(binary); 

		int decimal = 0; //변환된 정수
		int digit = 1; //각자리를 확인하기위한 비트
		_rrep(i, 29, 0) {
			if (binary[i]) decimal |= digit; //각 자릿수마다 정수로 변환
			digit <<= 1; //다음 자릿수를 탐색
		}

		maxXOR = std::max(maxXOR, decimal);
	}
	pr("%d", maxXOR);
}


int main(void) {
	func();

	rt 0;
}