개요

정렬된 자료를 절반씩 나눠가며 원소k의 위치를 찾는 탐색 알고리즘이다.
그리디 방법으로 탐색을 진행하면 O(N)이 걸릴것을 O(log N)에 마칠 수 있기때문에, 이후에 다른 알고리즘등에서 재사용이 많이되는 기본 탐색 알고리즘이다.

작동원리

정렬된 연속된 자료가 필요하다.
탐색범위의 양 끝 인덱스를 left, right로 둔다.
이때 가운데 인덱스에 해당하는 원소가
찾으려는 원소 k와 같은지, 작은지, 큰지에 따라 탐색 범위를 줄여나가는 원리이다.
arr = {0, 10, 20, 30, 40, 50, 60}인 자료와, 찾는원소 k=50이라고 하면 아래와 같은 그림이다.

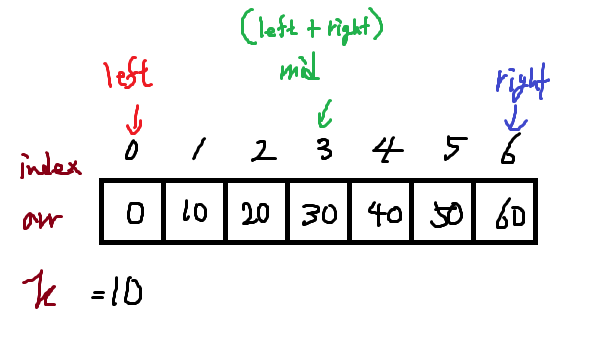
이때 매 탐색마다 arr[mid] == k ? 인지 확인하게된다.

위 그림에선 arr[3] == 10 ? ==> 30 > 10 이므로 왼쪽범위를 살피어 아래와 같다.

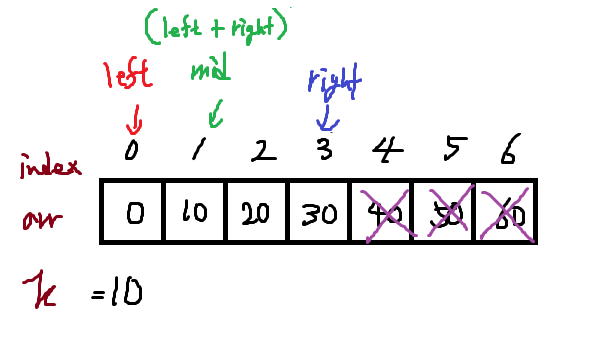
이번에는 arr[1] == 10 ? 일치하므로 찾은것이다.

이때 반대로 arr[mid] < k 이 나온다면은 오른쪽 범위를 탐색하게되어
left = mid + 1로 인덱스를 바꾸고 탐색을 이어가게 된다.

Lower Bound

이진탐색이 특정원소 k의 위치를 찾는것이라면,
Lower Bound, Upper Bound는 특정원소 k가 들어갈 정절한 위치를 찾는 알고리즘이다.

위와같은 수열 arr={1, 3, 5, 7, 9, 11, 13}과 k=8일때 lower bound를 수행해보자.

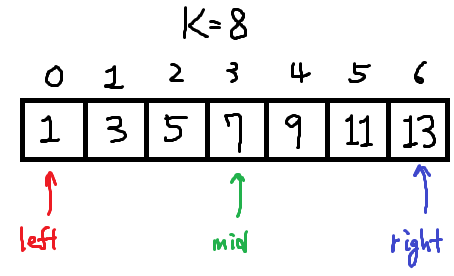
arr[mid] == k ? : arr[mid] < k
right 유지, 이진탐색과달리 left = mid + 1로 수정하고 탐색을 이어 진행한다.
(이진탐색에서는 같은 조건일때 left = mid 였었다.)

arr[mid] == k ? : arr[mid] > k
left 유지, 이진탐색과 달리 right = mid로 수정한다.
(이진탐색이면 right = mid-1 이다)
이것은 원소k가 처음 들어갈 수 있는 위치를 구하는것으로. 현재
arr[mid] = 11 즉 11이 지워지고 k가 들어갈 수 도 있다!!
탐색을 이어가자.

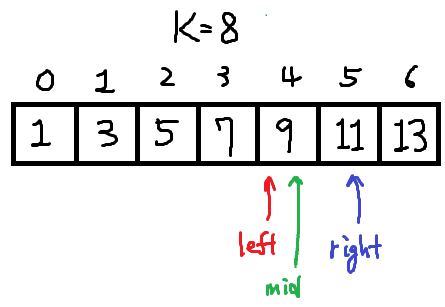
arr[mid] == k ? : arr[mid] > k
left 유지. right = mid로 수정한다.
이 또한 arr[mid] = 9인데 9자리에 k=8이 삽입될 수 도 있다.
공교롭게도 left == right이므로 탐색은 종료되고,
9가 있던 인덱스4가 k=8이 들어갈 수있는 최소 인덱스가 된다.
찾은 인덱스 = 4

왜냐면 Lower Bound는 원하는값 k이상(같거나 큼) 값이 처음 나오는 위치 인덱스를 찾는것이기 때문이다.

아래는 소스코드이다.

//arr에서 k이상인 값이 처음나오는 인덱스를 찾는 함수
	int LowerBound(vector<int>& arr, int k) {
		int left = 0, right = arr.size() - 1;

		while (left < right) {
			int mid = (left + right) / 2;
			if (k <= arr[mid]) //k이상인값이 나오면
				right = mid; 
			else
				left = mid + 1;
		}

		return right;
	}

Lower Bound를 이용한 Binary Search 구현

//arr에서 원소k의 위치인덱스를 찾아서 리턴하는 함수
	int BinarySearch(vector<int> &arr, int k) {
		int left = 0, right = arr.size() - 1;
		while (left <= right) {
			int mid = (left + right) / 2;
			if (arr[mid] == k)
				return mid;
			else if (k < arr[mid])
				right = mid - 1;
			else if (arr[mid] < k)
				left = mid;
		}
		return -1; //찾지 못하였음.
	}

Upper Bound

Lower Bound와 비슷하나, 찾는값k 초과인 첫번째 인덱스를 찾는 알고리즘을 뜻한다.

if(k < arr[mid]) 로 조건하나만 수정하면되므로 바로 구현코드를 올리겠다.

//arr에서 k초과인 값이 처음나오는 인덱스를 찾는 함수
	int UpperBound(vector<int>& arr, int k) {
		int left = 0, right = arr.size() - 1;

		while (left < right) {
			int mid = (left + right) / 2;
			if (k < arr[mid])
				right = mid;
			else
				left = mid + 1;

		}

		return right;
	}

마치며

앞서 이진탐색, LowerBound, UpperBound를 살펴보았다.
정리를 하자면 수열 arr에서 원소k가 존재할때
이진탐색은 그 위치인덱스 i를 찾고
LowerBound는 i-1를, UpperBound는 i+1를 찾을 것이다. 이를 그림으로 나타내보면 아래와 같다.

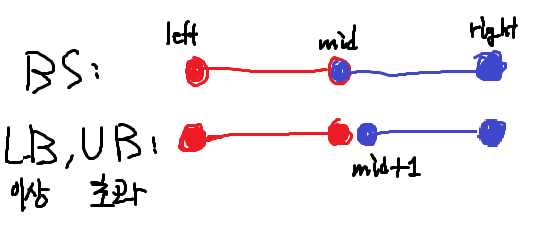
수학에서 쓰이는 포함, 초과를 그려본것이다. 각구간은
왼쪽구간으로 좁혀질때의 범위는 빨간색으로
오른족구간으로 좁혀질때의 범위를 파란색으로 그려본것이다.
LowerBound, UpperBound의 정의는 이상, 초과 인것을 잊지말자.
사실 이 두가지는
C++에 <algorith> 헤더에 std::lower_bound, std::upper_bound가 이미 구현되 있다.
하지만 다른 알고리즘에서도 종종 나오는 개념이므로
익숙해질 필요가 있다. 모든 탐색의 근간이되는 알고리즘이지 않을까 싶다.

구간을 잘 기억하자
left = mid // right = mid-1