개요

수열 arr의 모든 부분수열중 원소가 모두 증가하는 부분수열의 최대길이를 구하려는 문제가 있을때,
단순히 전부 그리디방법으로 탐색시, N N회의 연산이 필요하나,
DP를 이용하여 N N (1/2)로 절반으로 줄이거나
BS(Binary Search)를 이용하여 N log N 의 연산만에 해결 가능하다.
그외에 세그먼트트리를 이용한 방법도 있으나 여기선 DP, BS 두가지경우만 소개하려고한다.

DP를 이용한 LIS 알고리즘

DP[i] = "0~i원소로 이루어진 부분수열내의 LIS의 길이" 로 정의하면,
Bototm-up으로 DP[i]를 구해두면, i보다큰 모든인덱스k에서 DP[i+k]이 arr[i] < arr[i+k]관계를 만족하면
DP[i+k] = DP[i] + 1이라는 간단한 수식을 생각해볼 수 있다.

따라서 알고리즘으로 구현하면 아래와 같다.

int LISwithDP(vector<int>& arr) {
		if (arr.empty()) return 0;

		vector<int> dp(arr.size());

		for (int i = 0; i < arr.size(); i++) {
			//i보다 작은 j에대해 모두 감소하는관계라면 
			//최소한 자기자신으로만 이루어진 LIS가 존재가능
			dp[i] = 1; 

			for (int j = 0; j < i; j++) 
				if (arr[j] < arr[i]) 
					dp[i] = max(dp[i], dp[j] + 1);
		}
		
		return dp[arr.size() - 1];
	}

이때 arr의 모든 부분수열에서 LIS는 최소한 자기자신만으로 이루어질 수 있으므로 초깃값으로 1을 지정해주어야한다.

이분탐색을 이용한 LIS 알고리즘

먼저 수열arr을 전부 순회하기에 O(N)이 소요되는데,
이때 각 원소마다
list배열에서 lower_bound로 적절한 위치를 찾아서 (lower_bound알고리즘 >> https://velog.io/@cldhfleks2/Binary-Search)
arr의 원소를 기록하기에lower_bound를 사용해서 O(log N)
총 O(N log N)의 시간복잡도 안에 해결 가능해진다.
자세히 살펴보자.

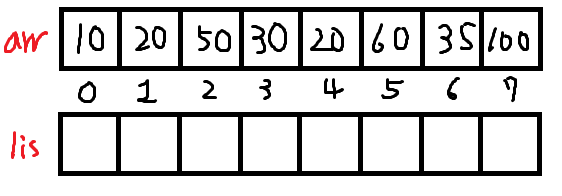
arr과 같은 크기의 lis 배열을 준비한다.
이제 두가지 동작을 수행할것이다.

1. lis의 끝원소보다 arr[i]가 크면 lis끝원소 뒤에 추가한다.
2. lis의 끝원소보다 작거나 같으면 lower_bound를 찾아 그 위치에 arr[i]를 덮어씌운다.

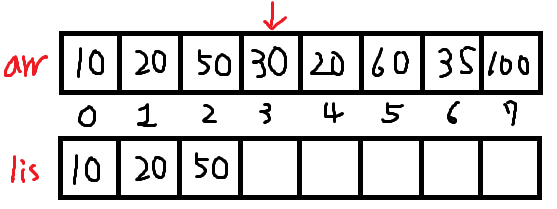
arr[0]~arr[2] 은모두 증가하므로 lis에 차례대로 넣었다.
이제 arr[3]을 보는데, 이것은 lis의 끝원소 50보다 작으니 lower_bound위치에 arr[3]을 덮어씌운다.

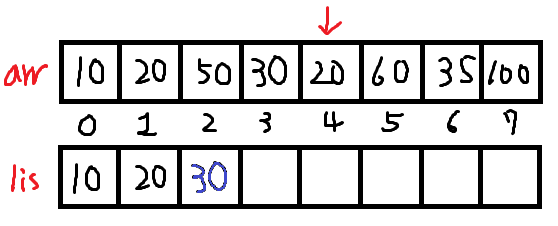
그리고 arr[4]를 보면 이 또한 작거나 같으므로 lower_bound인 lis[1]에 덮어씌운다.

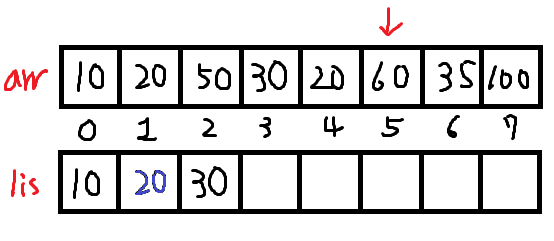
arr[5]는 크므로 lis맨뒤에 추가한다.

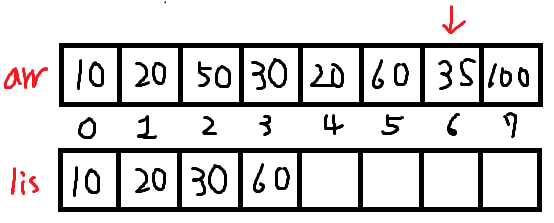
arr[6]은 60보다 작으니 lower_bound인 lis[3] 에 덮어씌웁니다.
이로써 알 수 있는것이 lis에 lower_bound를 찾아 원소를 덮어씌웠기때문에,
arr[2] = 50이 lis의 맨뒤에 존재했다면 arr[6]을 추가하지 못했으니 LIS가 아니게 됩니다.
따라서 매번 lis 배열이 증가하는 수열이 될수있도록 최적의 위치를 찾도록, 큰값은뒤, 작거나같은값은 적절한위치를 찾아 덮어씌우기에 LIS를 유지 할 수 있습니다.

이제 코드를 보자.

//아래의 LIS에 사용될 LowerBound함수
	int LowerBound(vector<int>& lis, int k) {
		int L = 0, R = lis.size() - 1;
		while (L < R) {
			int M = (L + R) / 2;
			if (k <= lis[M])
				R = M;
			else
				L = M + 1;
		}
		return R;
	}

	//2. LowerBound를 이용하여 LIS를 구하는 함수
	//만들어진 LIS배열은 순서가 뒤섞인, 
	//그저 arr의 어떤 요소가 LIS를 이루는지만 확인 가능
	int LISwithBinarySearch(vector<int>& arr) {
		if (arr.empty()) return 0;

		vector<int> lis(arr.size());
		lis.push_back(arr[0]);
		for (int i = 1; i < arr.size(); i++) {
			if (lis.back() < arr[i]) 
				lis.push_back(arr[i]);
			else //lis에 arr[i]가 들어갈 적절한위치를 LowerBound로 찾아서
				//해당위치에 arr[i]를 저장
				lis[LowerBound(lis, arr[i])] = arr[i]; 
		}
		
		return lis.size(); //만들어진 lis 배열을 리턴합니다.
	}

이방법은 DP를 활용한 LIS와 달리, 그 길이와 LIS를 이루는 원소가 무엇인지 확인 가능합니다.
다만 만들어진 LIS배열의 원소는 원래 arr에서 옮겨진 순서가 섞여있다.

관련문제

https://www.acmicpc.net/problem/11053 >> https://velog.io/@cldhfleks2/11053