Algorithm
1.[Algorithm] Seqment Tree 세그먼트트리
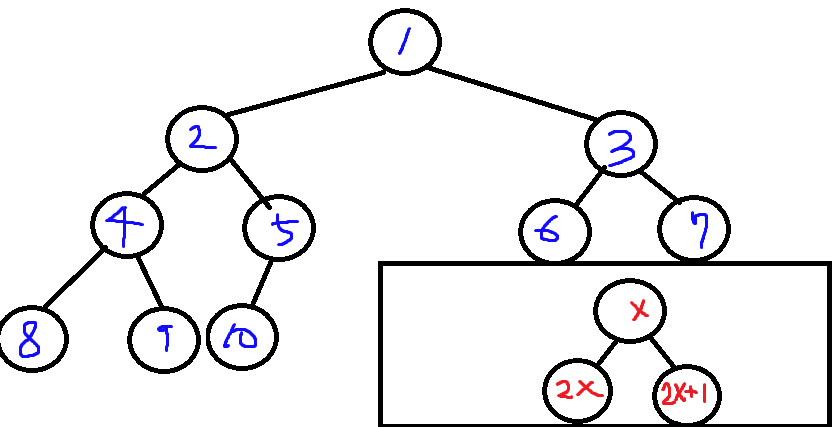
참고 : https://www.acmicpc.net/blog/view/9 개요 세그먼트트리는 배열 A가 있을때, 배열 원소를 업데이트하며 구간합을 구해야할때 사용한다. 세그먼트트리를 이용하지 않은경우, M번업데이트하는데 O(M), 구간합을 구하는데 O(N) 총 O(NM
2.[Algorithm] DFS, BFS
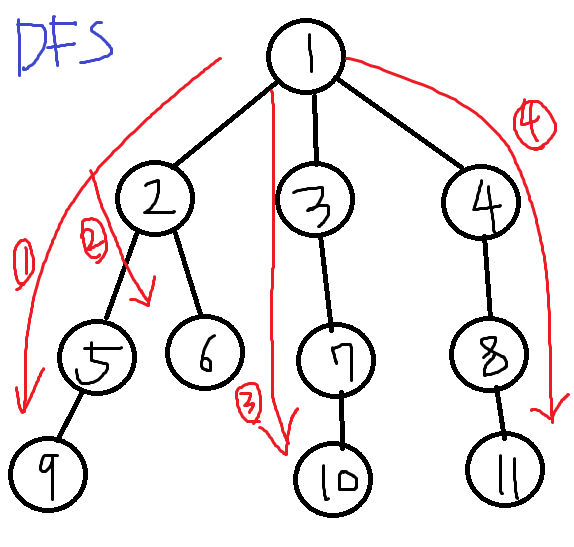
DFS, Depth First Search. 깊이우선탐색 정점의번호가 모두 유일할때, 현재 탐색중인 정점과 인접한 정점들을 정점번호가 낮은순으로 가장 깊이 탐색하는 방법이다. 그림에서보면알다싶이 같은 레벨(2-3-4, 5-6-7-8, 9-10-11)을 무시한채, 현재
3.[Algorithm] DSU, Disjoint Set Union&Find
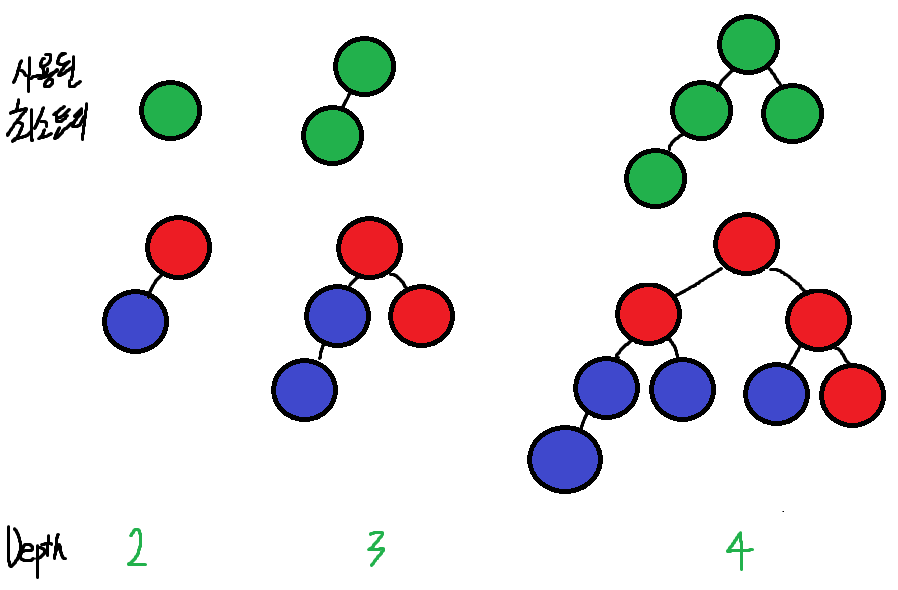
Disjoint Set(서로소 집합)은 서로 배타적인 원소를 가진 두 집합. 공통되는 원소를 가지지않은 두 집합을 말한다. 여기서 해당 알고리즘은 Disjoint Set 자료구조를 사용하여, 서로 다른 두 원소가 같은 집합에 속해있는지를 판별하는데 유용하게 사용된다.
4.[Algorithm] K-means clustering algorithm
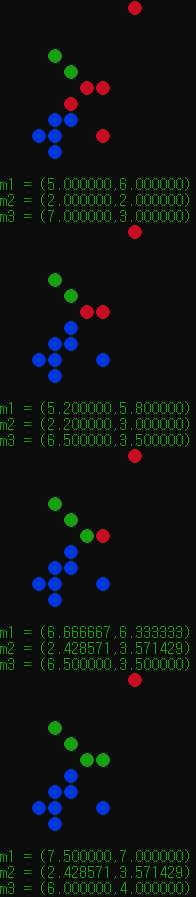
서론 기계학습 수업중에, K평균알고리즘이란것을 배웠다. 되게 직관적이고, 단순한 알고리즘이라 직접구현 해볼만하다는 생각에 C언어로 도전해봤다. 알고리즘 먼저 알고리즘의 작동 순서는 아래와같다. > 0. 각샘플들을 입력받는다.(필자는 2개의 특징벡터를 가지고 이를 각각 x, y로 제한하였다.) K개의 클러스터 중심점을 입력받은 샘플중에서 정한다. (이 또...
5.[Algorithm] Sprague-Grundy Theorem

서론 게임이론중 하나로, 단 두명의 플레이어로 이루어질때, 두 플레이어 모두 필승법을 알고있으면 누가 이길것인가? 를 다루는 이론이다. 조건 두명의 참가자만 진행 두 참가자가 차례를 번갈아 진행 두 참가자가 게임에 대한 모든 정보를 공유, 필승법을 인지 하고있음 자신의 차례에 할 수 있는 행동이 단 하나도 없다면 패배 유한한 게임 진행 알고리즘 스프라그 ...
6.[Algorithm] 분할정복을 이용한 거듭제곱 (A^n의 효율적인 계산)

A^n (n은 자연수) 을 구하는 문제를 n번 곱해 푼다면 O(n)이 걸린다. 하지만 n을 2진수로 변환하면 특정한 규칙을 찾을 수 있다. 이처럼 변환된 지수의 비트하나씩 & 1 연산해서 값이 1이나올때만 그 수를 곱해주면 곱할수 n을 2의제곱씩 묶어서 계산이 가능하므로 O(log n)로 풀 수 있다. 실제로 구현하면 아래와 같다. 홀수가나오는것은 해당...
7.[Algorithm] Dijkstra, 다익스트라

개요 그래프에서 한정점A에서 다른정점B까지의 최단거리를 구하는 문제를 종종 마주치곤한다. 이런 최단거리문제는 보통 다익스트라 알고리즘(Dijkstra Algorithm) 플로이드 워셜 알고리즘(Floyd-Warshall Algorithm) 벨만 포드 알고리즘(Bellm
8.[Algorithm] Floyd-Warshall 플로이드-워샬

개요 V개의 정점과 양의가중치를 가지는 E개의 간선이있는 그래프에서 임의의 정점s 부터 그래프내의 모든 임의의 정점 e 까지의 최단거리는 다익스트라 알고리즘을 사용하여 구했었다. 이때 1차원테이블에 그 결과를 저장했었다. 이번에는 V개의 정점과 양또는 음의 가중치를 가지는 E개의 간선이 있는 그래프에서 임의의 정점s가 고정된것이아닌 그래프 내의 모든 점과...
9.[Algorithm] SCC, Strongly Connected Component 강한연결요소
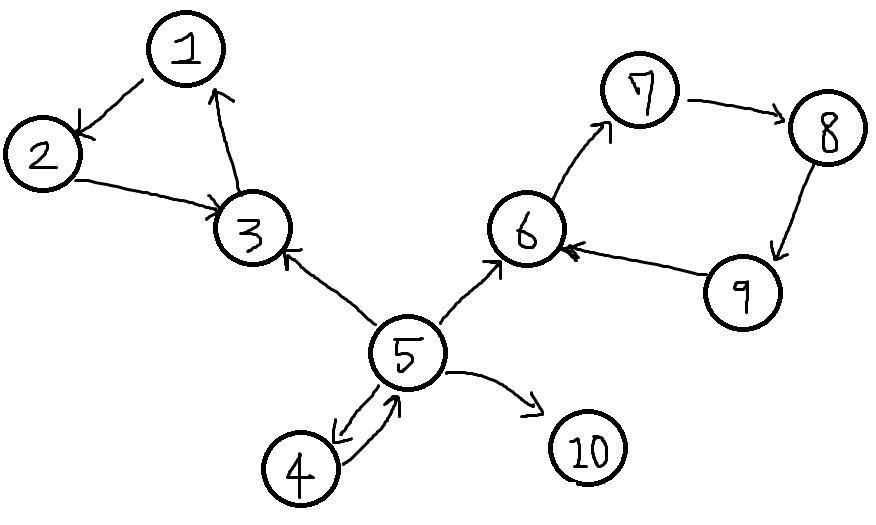
개요 SCC란. 보통 유향 그래프안에서 서로 강하게 연결되있는 부분집합을 의미합니다. 여기서 '강하게 연결되있는'이란 하나의 사이클이 형성되는 경우를 뜻하는데, 이런 하나의 SCC내의 두 정점 u, v는 서로에게 도달 할 수 있는 경로가 직접적/간접적으로 존재합니다.
10.[Algorithm] KMP, Knuth-Morris-Pratt 효율적인 문자열 탐색
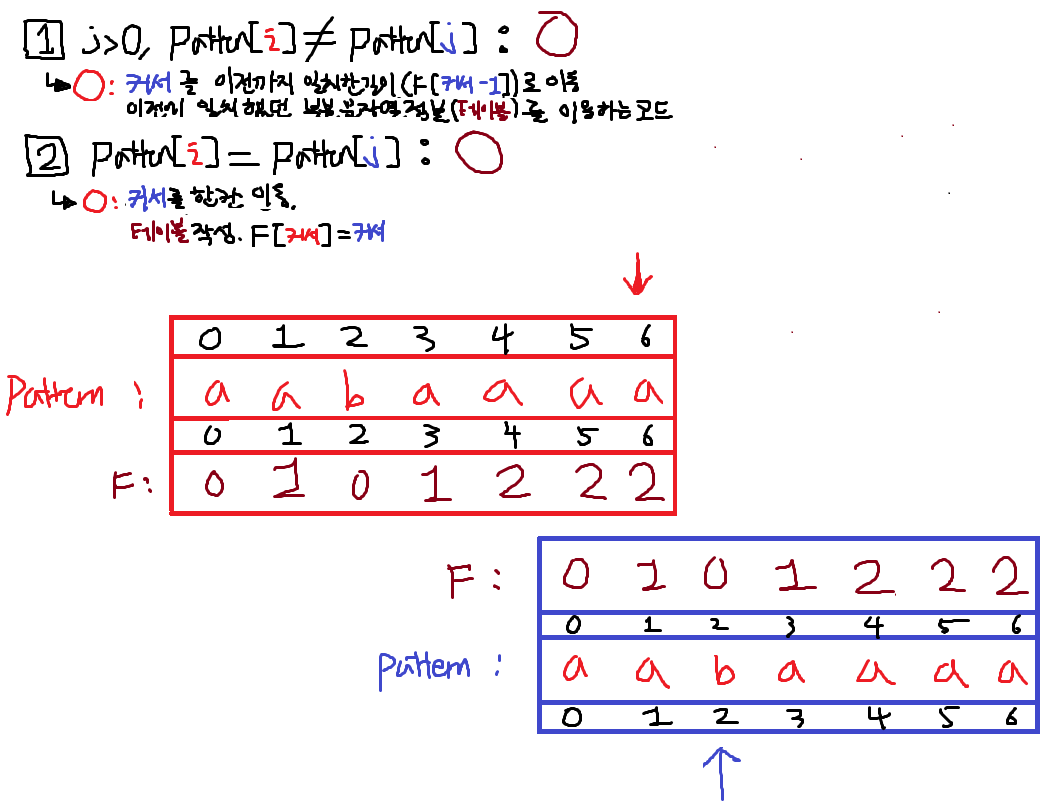
개요 보통 문자열내에서 원하는 단어(부분문자열)를 찾고자 할때 2중 for문을통해서 찾는다. (단어가 한글자인경우 이진탐색이나 트라이 자료구조를 사용한다.) 하지만 이런 연산은 본문자열의길이와 찾는문자열의길이가 길어짐에따라 비효율적인 O(N * M)이 걸리는 연산이다
11.[Algorithm] Trie자료구조
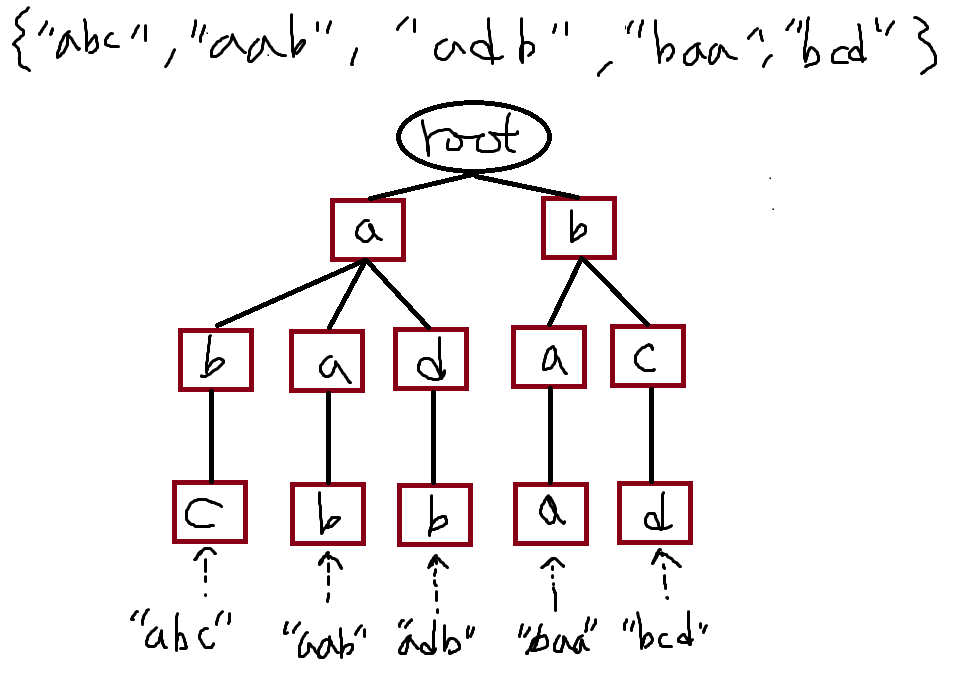
개요 문자열의 집합이 주어졌을때, 여기서 원하는 문자열을 탐색하려면 브루트포스방법으로 생각하면 문자열 갯수N, 문자열길이가 M이면 최대 O(N*M) 시간이 걸린다.(문자열길이는 제각각 다르겠지만..) 이것을 우리가 배운 이진트리를 이용하여 이진탐색을 한다고하면 한문자를
12.[Algorithm] LCS, Longest Common Substring 최장공통부분수열
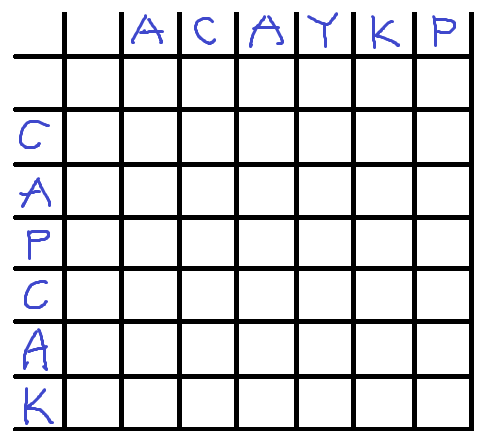
개요 주어지는 2개의 문자열의 서로 공통인 부분수열중 길이가 가장 긴것의 길이를 찾는 알고리즘이다. 이때의 부분수열은 연속되지않은 부분수열도 포함하여 LCS를 찾게된다. 이번에 소개할 LCS알고리즘을 사용하면 두 문자열의 길이 N, M에따른 O(N * M)만에 LCS를 찾을 수 있다. 작동원리 LCS알고리즘을 설명할때 자주쓰이는 두 문자열 'ACAYKP'...
13.[Algorithm] MSIS, Max Sum Increasing Subsequence

개요 수열 arr에서 연속되거나 그렇지않은 부분수열이 증가할때 해당 부분수열의 모든 원소의 합이 최댓값을 구하는 알고리즘이다. 최대 증가 부분수열 알고리즘이라고 한다. 구현 i보다 작은 j들을 하나씩 살펴보며, 현재 dp[i]값을 작성할것인데, 이때 arr[j]
14.[Algorithm] Binary Search, Lower Bound, Upper Bound
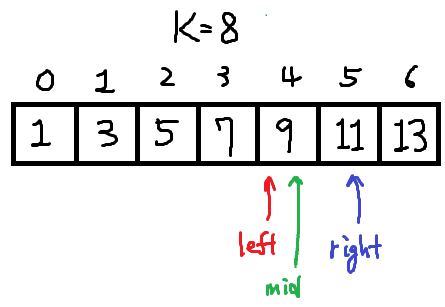
정렬된 자료를 절반씩 나눠가며 원소k의 위치를 찾는 탐색 알고리즘이다.그리디 방법으로 탐색을 진행하면 O(N)이 걸릴것을 O(log N)에 마칠 수 있기때문에, 이후에 다른 알고리즘등에서 재사용이 많이되는 기본 탐색 알고리즘이다.(정렬된 연속된 자료가 필요하다.)먼저
15.[Algorithm] LIS, Longest Increasing Subsequence
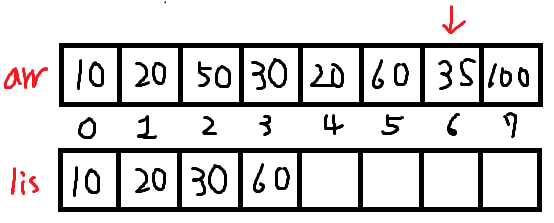
수열 arr의 모든 부분수열중 원소가 모두 증가하는 부분수열의 최대길이를 구하려는 문제가 있을때,단순히 전부 그리디방법으로 탐색시, N N회의 연산이 필요하나,DP를 이용하여 N N (1/2)로 절반으로 줄이거나BS(Binary Search)를 이용하여 N log
16.[Algorithm] Kruskal 크루스칼
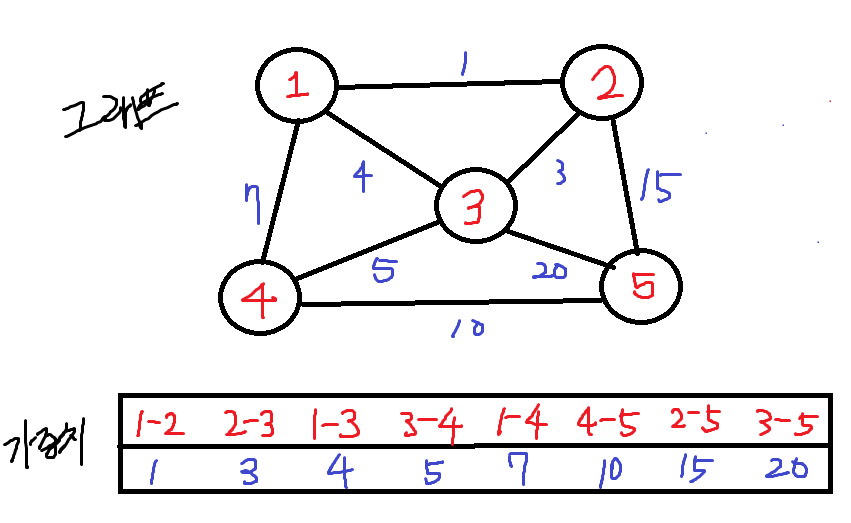
개요 여러 정점과 간선들로 이루어진 양방향 그래프가 있을때 부분 그래프가 최소한의 간선들로 이루어 졌을때 Spanning Tree, 신장트리라고 한다. 즉 Spanning Tree는 내부에 사이클이 없는 그래프를 의미하는것이다. 사이클이 생기는 순간 불필요한 간선이 하