개요
V개의 정점과 양의가중치를 가지는 E개의 간선이있는 그래프에서
임의의 정점s 부터 그래프내의 모든 임의의 정점 e 까지의 최단거리는 다익스트라 알고리즘을 사용하여 구했었다. 이때 1차원테이블에 그 결과를 저장했었다.
이번에는 V개의 정점과 양또는 음의 가중치를 가지는 E개의 간선이 있는 그래프에서
임의의 정점s가 고정된것이아닌 그래프 내의 모든 점과점 사이의 최단거리를 구하려고한다.(2차원 테이블에)
이때 쓰이는 알고리즘이 Floyd-Warshall 알고리즘이다.
실제로는 워샬의 알고리즘으로부터 영감을 받아 플로이드가 만들었다고 보아
Floyd 알고리즘이라고 줄여 부르기도 한다고 한다.
시간복잡도를 살펴보면
다익스트라알고리즘은 간선의 갯수가 E고 정점의갯수가 N이면
O(E log N) 의 시간복잡도를 가지나
플로이드워샬 알고리즘은 O(N^3)의 시간복잡도를 가진다. (간선의 갯수는 중요X)
왜냐면, 앞서말했듯이 2차원 테이블을 결과로만들며O(N^2), 이 과정을 모든 정점의 갯수 N만큼 반복하기 때문이다.
이때 2차원테이블을 갱신하는 과정에서 아래의 점화식이 쓰인다.
이 말은 즉 K가 1번부터 N번 정점까지 수행될때, 출발 정점 i로부터 해당 정점 K를 지나서 도착 정점j에 도달하는 경로의가중치합과 기존의 출발 정점i에서 도착 정점 j로 직행으로 가던 가중치값 중 최솟값으로 갱신한다는 것이다.
아래 동작과정에서 자세히 살펴보자.
동작과정
- 2차원 테이블 Wij를 i==j 인 경우에는 0, 그 외에는 무한한값으로 초기화한뒤 입력을받아서 테이블을 덮어씌운다.
(Wij = i에서 j로가는 가중치 w를 기록한것.)
결과적으로 입력받은 경로에는 유한한값이, 입력받지 않은값은 무한한값(INF)가 저장된다.
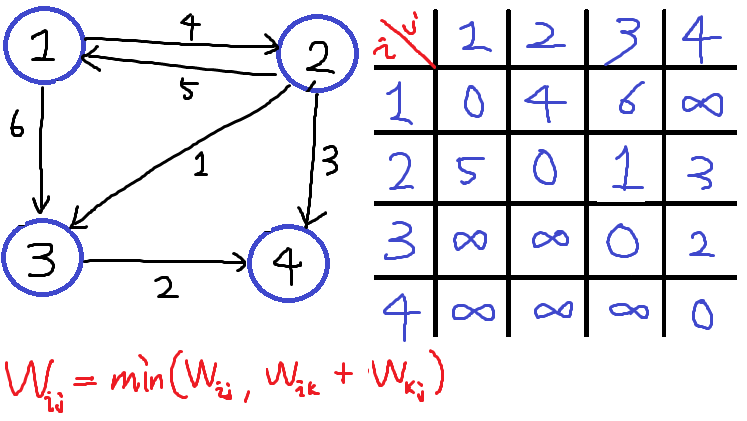
1. K=1 . 즉 1번노드를 거쳐가는 모든 경우를 살펴보자.
4x4 = 총 16개가 계산된 모습이다. 초록색 사각형이 최솟값으로 채택된 값이다. 아무것도 갱신되지 않고있다.
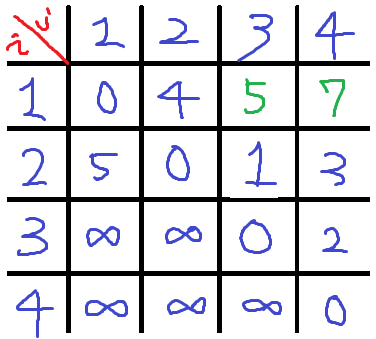
2. K=2 2번노드를 거쳐가는 경우를 살펴해보자. 이번에는 갱신되는 부분만 칠해보았다.
즉 W13 일때 중간에 2번노드를 거쳐가면 최단거리가 갱신되며,
W14일때는 2번노드를 거쳐거면 직행으로는 못가던길을 우회해서 갈 수 있음을 나타낸다.
이에 따라 테이블을 갱신해보자.
3. 위 방법대로 K=3, K=4 일때를 반복해보면 각각 아무것도 갱신되지 않음을 알 수 있다.
알고리즘의 동작 과정이 어렵진않으나 중요한점은
중간에 거쳐가는 노드 K가 1부터 N 까지 순차적으로 순회한다는 점이다.
만약 K가 N부터 1로 내림차순 순회한다면??
'답은 상관없다' 이다.
구현
W테이블에 입력을 받은뒤(입력값이 있으면 받고, 그외에 값은 i==j 일때는 0 나머지는 무한한값INF)
간단한 3중첩 반복문으로 쉽게 구현 할 수 있다.
관련 문제
https://www.acmicpc.net/problem/11404 >> https://velog.io/@cldhfleks2/11404
https://www.acmicpc.net/problem/11403 >> https://velog.io/@cldhfleks2/11403
