[Algorithm] SCC, Strongly Connected Component 강한연결요소

이성훈·2022년 10월 26일
DFSStrongly Connected Componentalgorithmscctarjan's algorithm강한연결요소재귀
3

Algorithm

목록 보기
9/16

개요

SCC란. 보통 유향 그래프안에서 서로 강하게 연결되있는 부분집합을 의미합니다.
여기서 '강하게 연결되있는'이란 하나의 사이클이 형성되는 경우를 뜻하는데, 이런 하나의 SCC내의 두 정점 u, v는 서로에게 도달 할 수 있는 경로가 직접적/간접적으로 존재합니다.

결론적으로 유향 그래프안에서의 모든 정점은 각각이 SCC가 되도록 분할이 가능합니다.

사실 무향 그래프에서도 SCC정의는 가능하나 무향 그래프 전체가 하나의 SCC로 분류되기에 큰 의미가 없습니다.


아래의 그림을 봅시다.

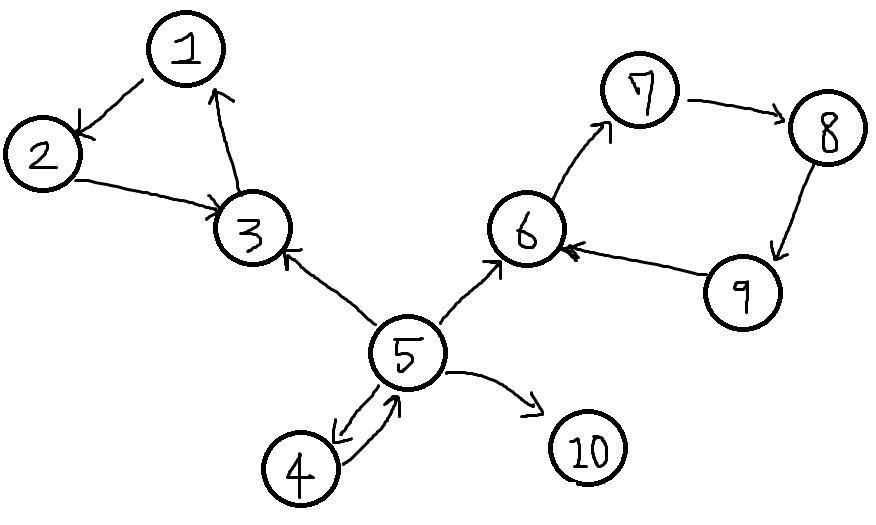
이 그래프에서 사이클이 생기는 부분집합은 {1, 2, 3}, {6, 7, 8, 9}, {4, 5}인데 이것이 SCC가 됩니다. 그리고 혼자있는 정점 10번 또한 하나의 SCC로 분류 됩니다.
따라서 위 그래프에서 각각 SCC마다 그룹핑하여 표기하면 아래와 같습니다.
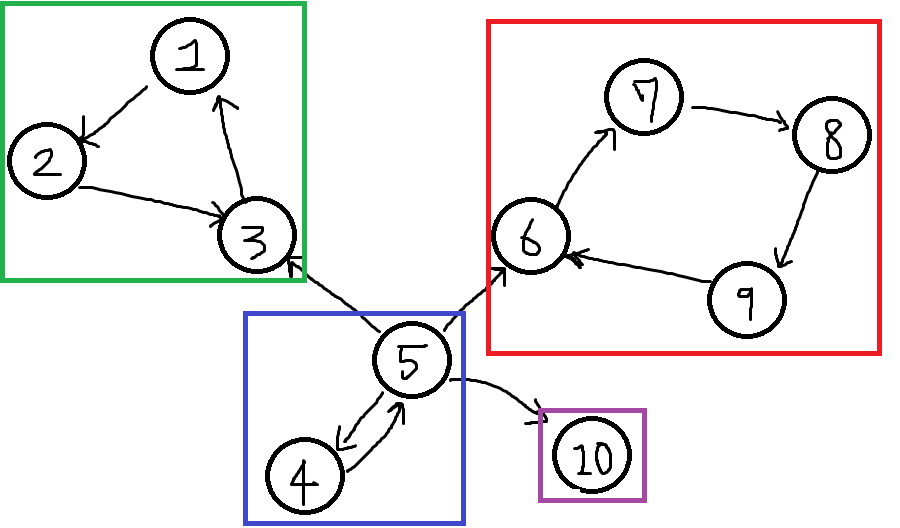만약 10번과같은 정점처럼 그냥 동떨어져 있는 정점만 존재하는 그래프라면 SCC는 어떻게 이루어질까요?

사이클이 없어도 각각 정점이 하나의 사이클처럼 SCC로 분류됩니다.

이제 이런 SCC를 추출하는 알고리즘중 대표적인 타잔 알고리즘(Tarjan's Algorithm)을 알아보겠습니다.
코사라주 알고리즘(Kosaraju's Algorithm))또한 SCC를 추출할 수 있으나, 가장 일반적인것은 타잔 알고리즘입니다.

타잔 알고리즘 개요

타잔 알고리즘은 모든 정점에대해 DFS를 수행하며 스택을 통해 SCC를 분리 해내는 알고리즘입니다.
여기서 각 정점마다의 부모노드가 무엇인지 기록하는 일이 필요합니다.
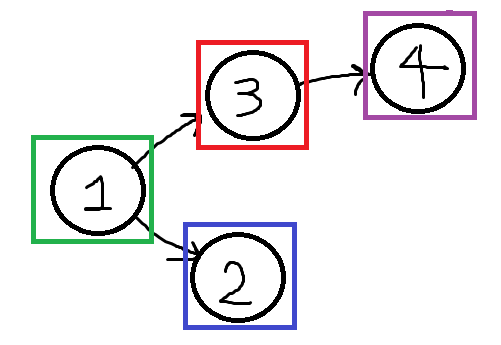
아래와 같은 경우를 봅시다.
이 경우의 {1, 2, 3, 4}는 서로 사이클이 없기에 SCC가 아닙니다.
정확히 말하자면 각 정점간 부모노드번호를 저장하는 P[x]를 설정하면(초깃값은 자기자신) P[1]=1 P[2]=1 P[3]=2 P[4]=3입니다. 이때 자기자신의 부모노드로 가는 경로가 있으면 그 정점은 SCC에 속하는것입니다.
위 경우에선 사이클이 없으므로 어느 정점을 골라도 그 끝만 4번정점을 향할뿐 P[x]번 정점에 도달 하지 못합니다.

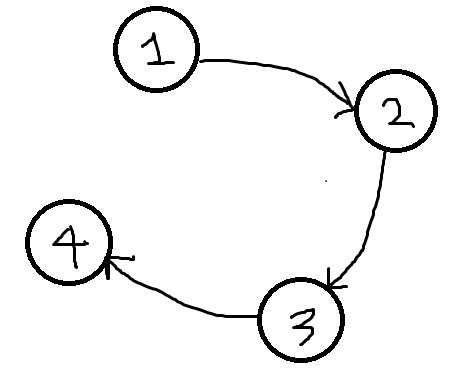
이제 4 -> 1로 가는 간선을 하나 추가하면 사이클이 생기겠죠?
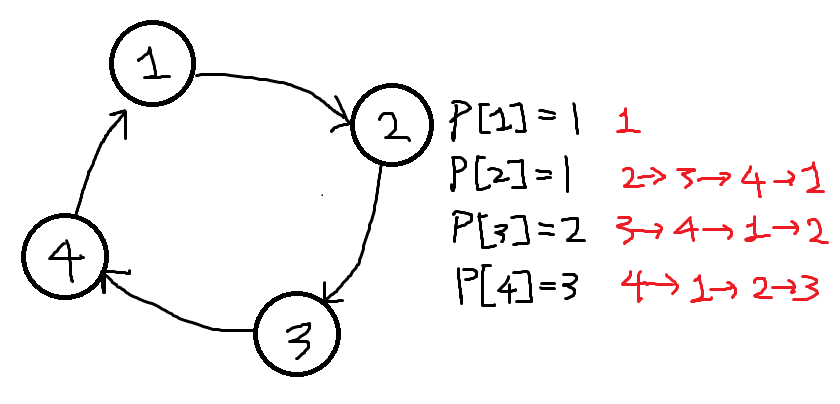이렇게 생긴 사이클 덕분에 빨간색으로 그린 경로를 따라 각각 자기부모노드로 가는 경로가 생겼습니다.
이것이 의미하는 바는, 사이클내의 두 정점 u, v은 서로 도달 가능한 경로가 있음을 의미합니다.

타잔 알고리즘 작동 방식

이제 타잔 알고리즘의 작동 방식을 살펴봅시다.

  • 정점번호가 낮은 순으로 DFS를 탐색할것입니다.
  • 현재 정점의 부모노드를 설정, 스택에 넣습니다.
  • 현재 정점으로부터 도달가능 한정점으로(연결되있고, finished == false인 정점) DFS탐색합니다.
  • DFS를 마친후에 P[x] == x인 점은 하나의 SCC입니다.
  • SCC를 찾았으니 스택에서 해당 x가 나올때까지 POP하며 동시에 finished[x] = true설정합니다.
  • 찾은 SCC를 저장하고 DFS함수는 자신의 부모노드를 리턴합니다.(그래야 DFS탐색에 사용됨)


    이제 이것을 위에서 보여준 유향 그래프를 보며 하나씩 살펴봅시다.


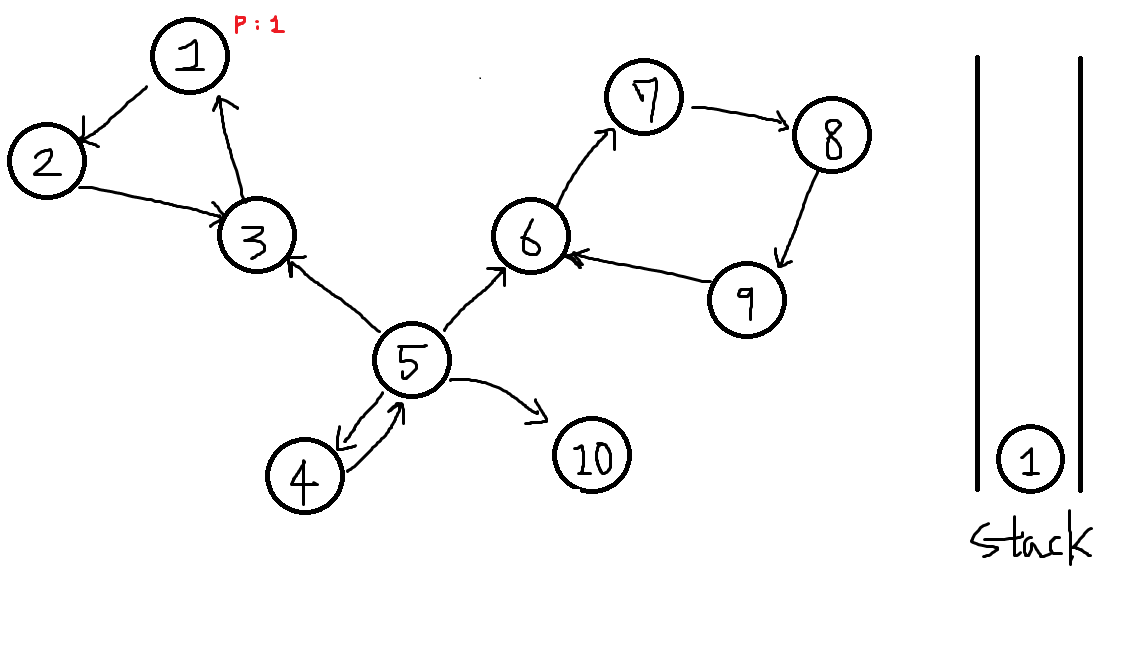
  1. 맨처음 임의의 정점으로부터 시작하며 모든 정점을 한번씩 돕니다. 여기선 1번정점부터 탐색을 시작했습니다.
    모든 정점의 finished[x] = false이고 P[x] = 0이나 음수로 설정되있습니다.

  2. 1번정점을 선택하며 도달가능한 모든 정점들에대해 DFS를 수행합니다.
    이때 정점번호가 낮은 순으로 먼저 탐색하며,
    탐색하자마자 해당 정점의 부모노드P[1] = 1. 자기자신으로 표기합니다.
    또한 스택에 자기자신을 넣습니다.

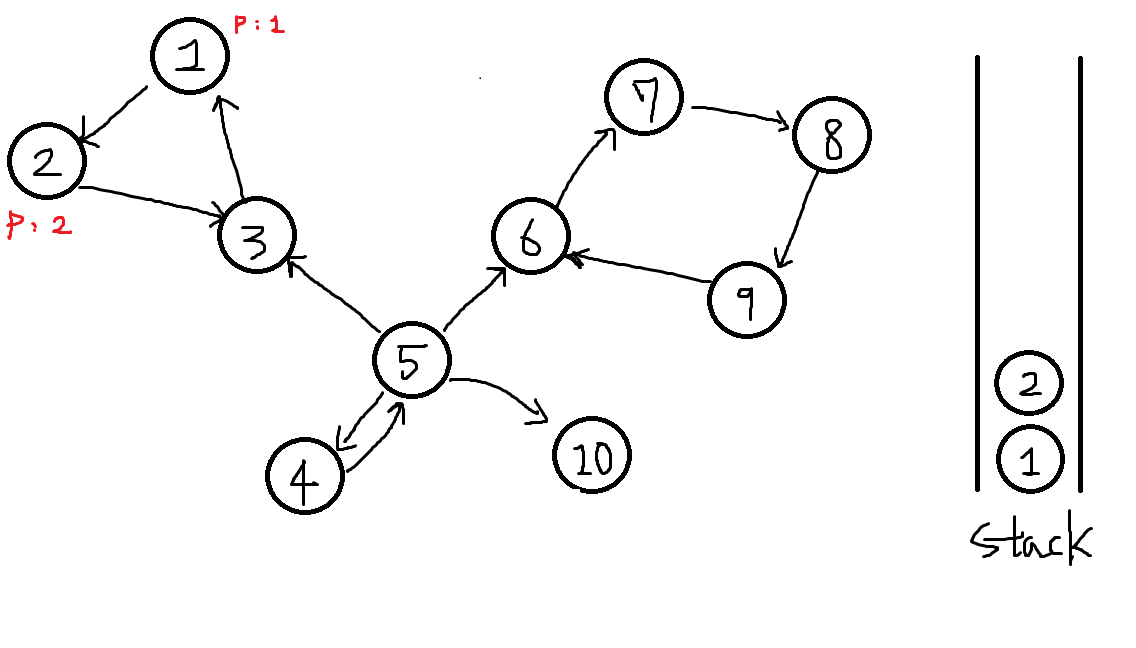
  3. 1번에서 도달가능한 2번정점을 탐색합니다.
    부모노드 P[2] = 2 자기자신입니다. 또 스택에 자기자신을 넣습니다.

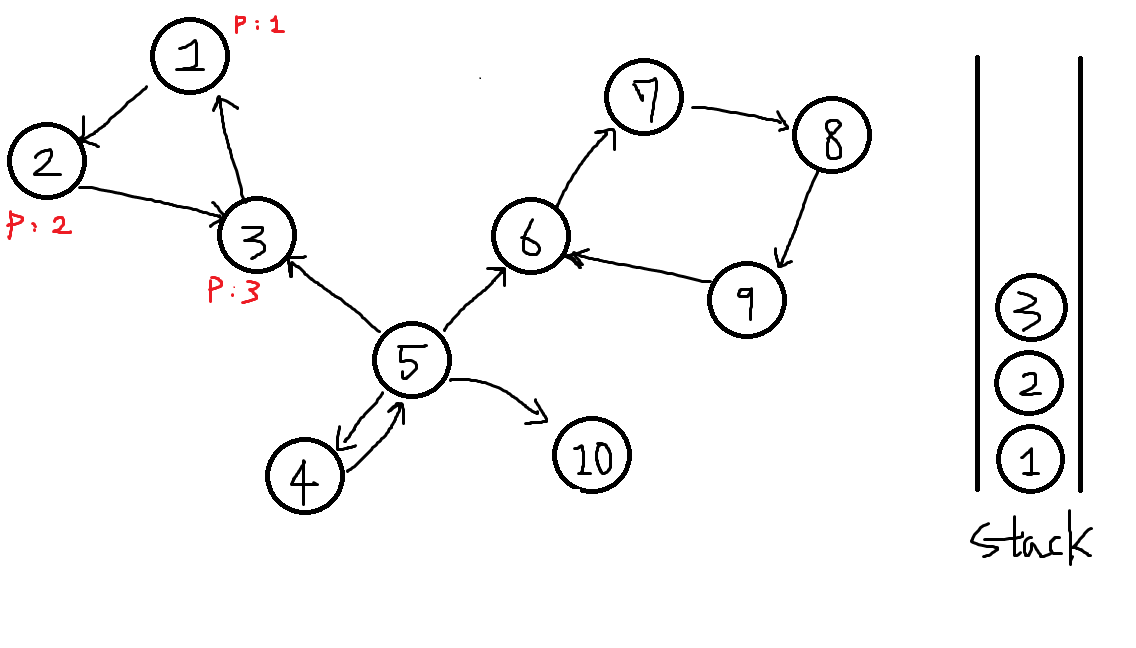
  4. 2번에서 도달가능한 3번을 탐색합니다.
    이 또한 P[3] = 3, 스택에 3을 넣습니다.

  5. 이제 3에서 도달가능한 정점중 1번을 탐색하려다가
    P[1] != 0 이므로 P[3] = P[1] = 1 로 수정됩니다.
    이제부터는 탐색하던 방향의 역순으로 거슬러가 부모노드를 전부 수정합니다.
    이때 아직 DFS가 끝나지않음을 의미하는 finished == false입니다.

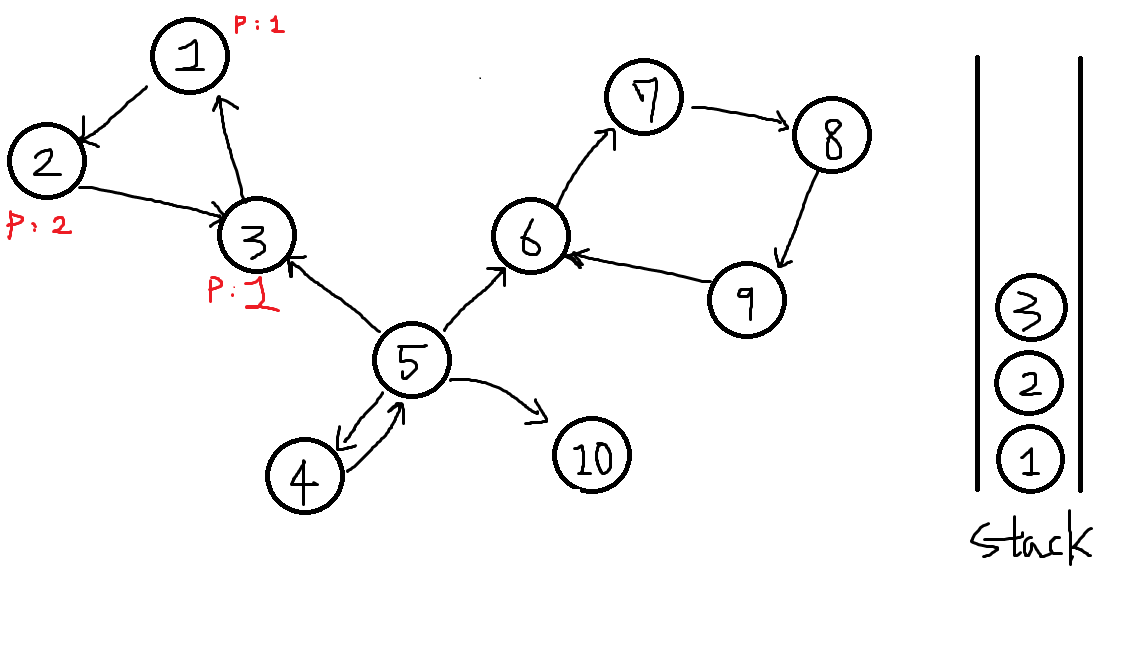
  6. 역순으로 이전에 탐색하던 2번 정점을 확인합니다.
    2번 정점의 부모값은 3번에서 넘어온 1번으로 갱신됩니다.
    P[2] = P[3] = 1

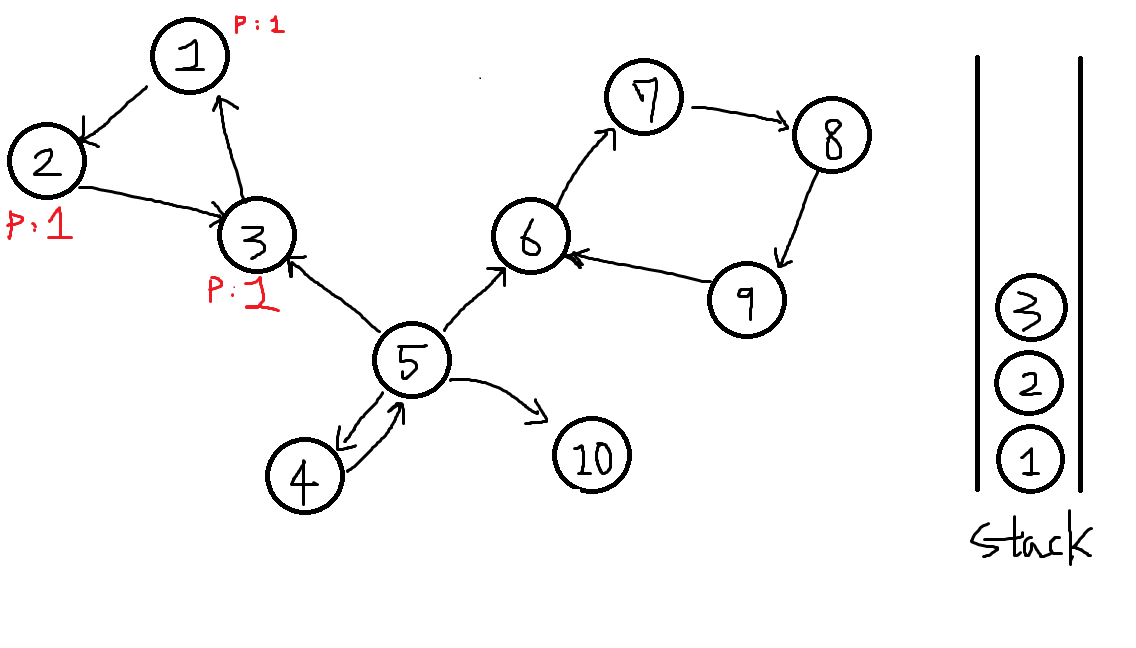
  7. 이번에도 2번에서 거슬러올라가 1번정점으로 가는데
    P[1] == 1, P[x] == x를 찾았습니다. P[x] == x 가 의미하는 것은 자기자신이 하나의 SCC에서 부모노드의 역할을 한다는것입니다.
    따라서 스택에서 자기자신이 나올때까지 하나씩 POP하면 그것이 모여 하나의 SCC가 됩니다.

    6-1. 이제 스택에서 자기자신인 1번이 나올때까지 뽑습니다.
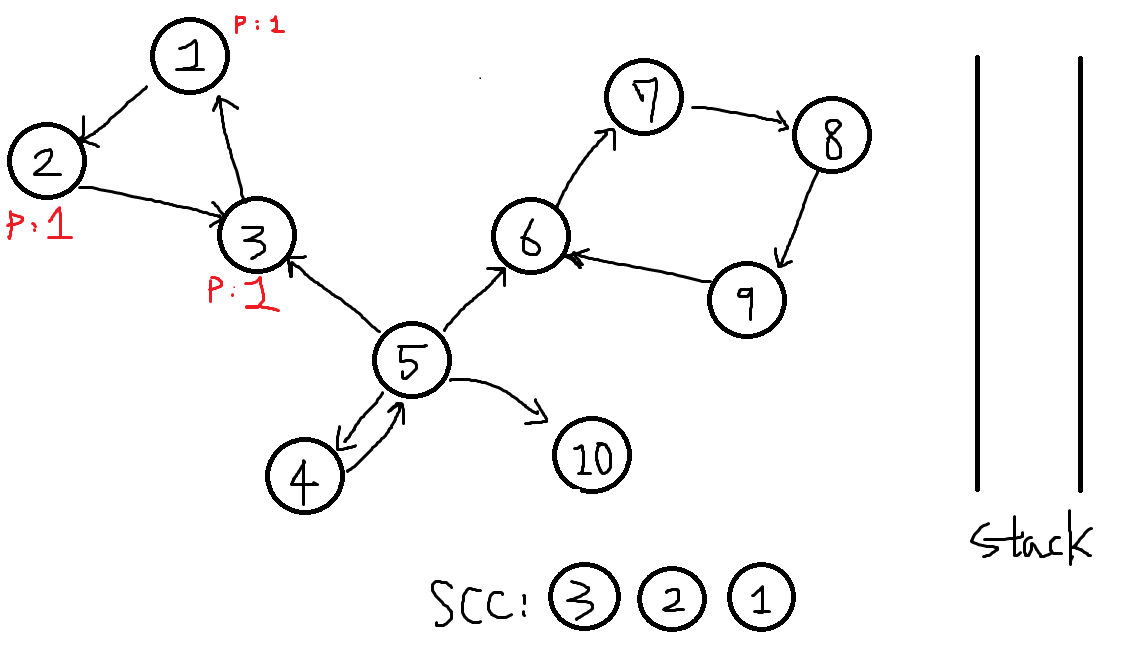    {3, 2, 1}이 하나의 SCC로 분류됩니다.

    6-2. 뽑은동시에 각 정점번호마다 finished값을 true로 바꿔줍니다.

  8. 이제 DFS를 하지않은 정점들(finished == false인 정점들)중 가장 낮은 정점인 4번을 탐색합니다.

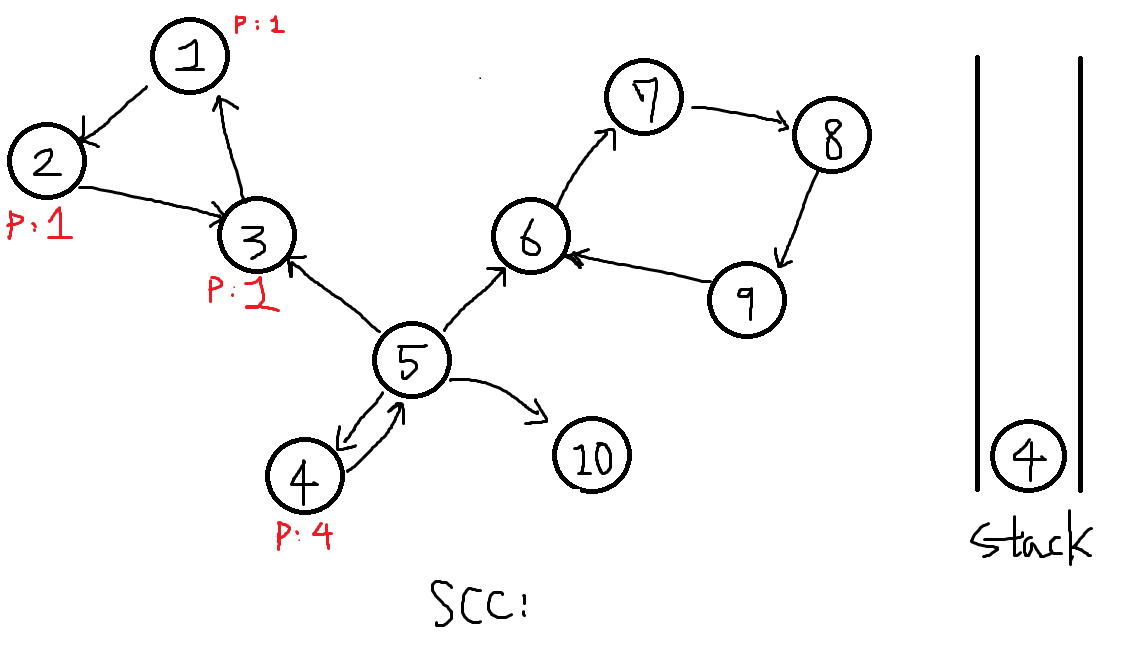
  9. 이어 도달가능한 5번 정점을 탐색합니다.

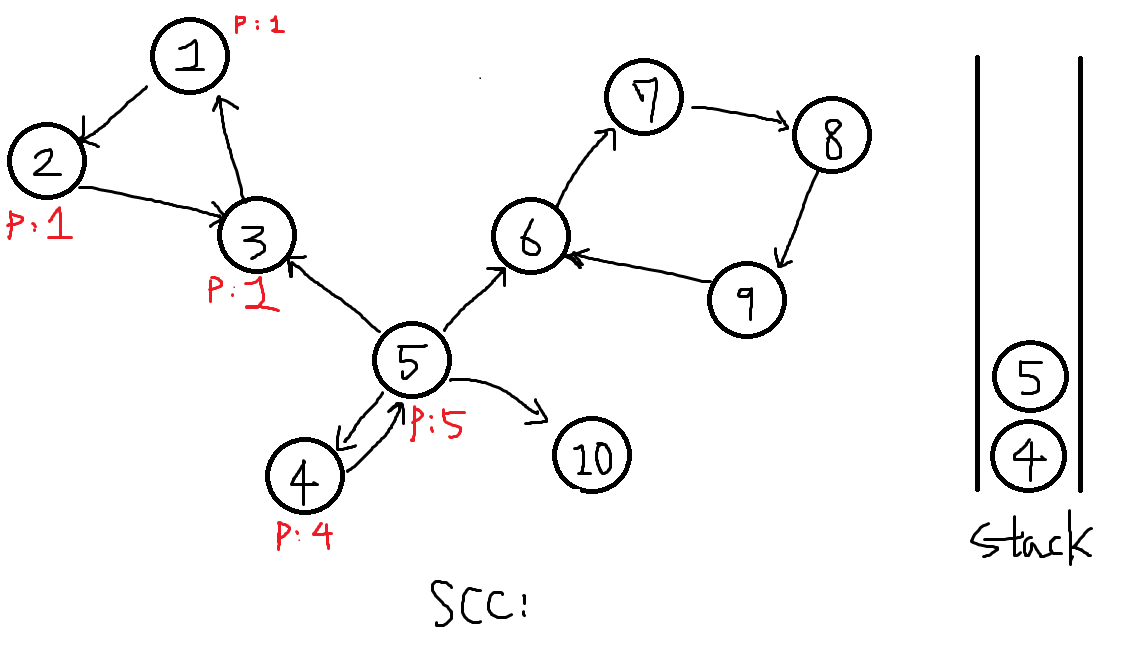
    이다음으로 도달가능 한 점은 3, 4, 6, 10 이있는데,
    이중 finished = true인 점은 제외하여 4, 6, 10입니다.
    이중 가장 낮은 번호인 4번 먼저 탐색합니다.

    8-1. 4번을 탐색하려는데 P[4] != 0 이므로 현재 정점5의 부모를 다음 정점4번으로 설정합니다.P[5] = 4

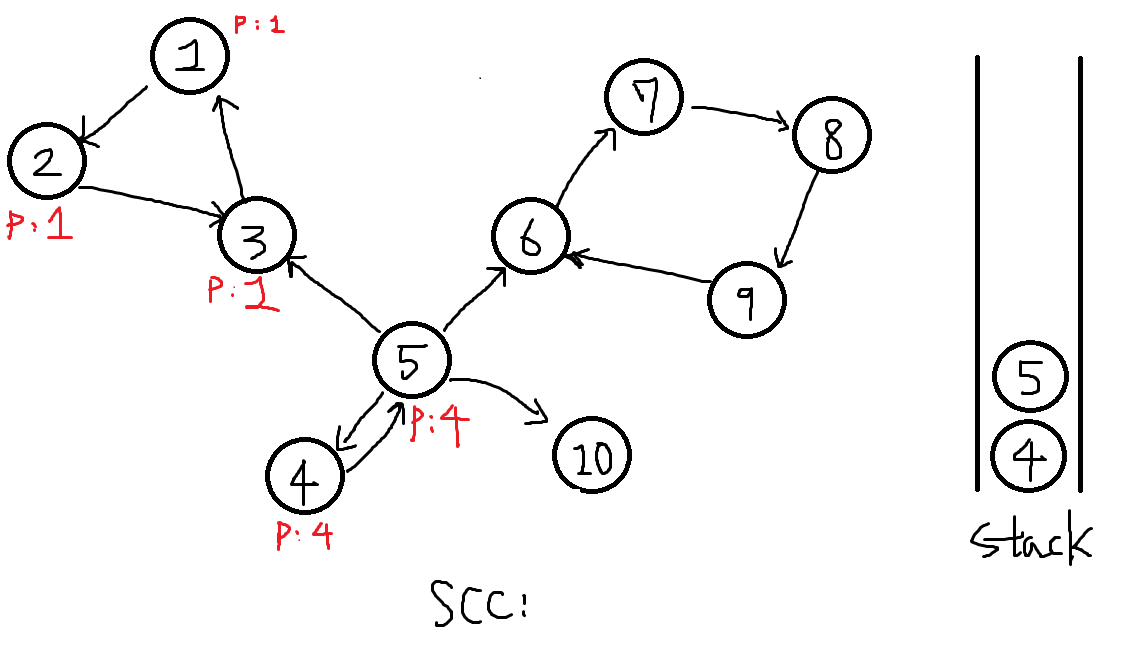
    8-2. 역순으로 거슬러서 이전 정점인 4번을 탐색합니다. 그런데 P[4] == 4, P[x] == x이므로 4번이 또 하나의 SCC의 부모노드값입니다. 이제 SCC를 추출할 차례입니다.
    스택에서 4번이 나올떄까지 POP합니다.
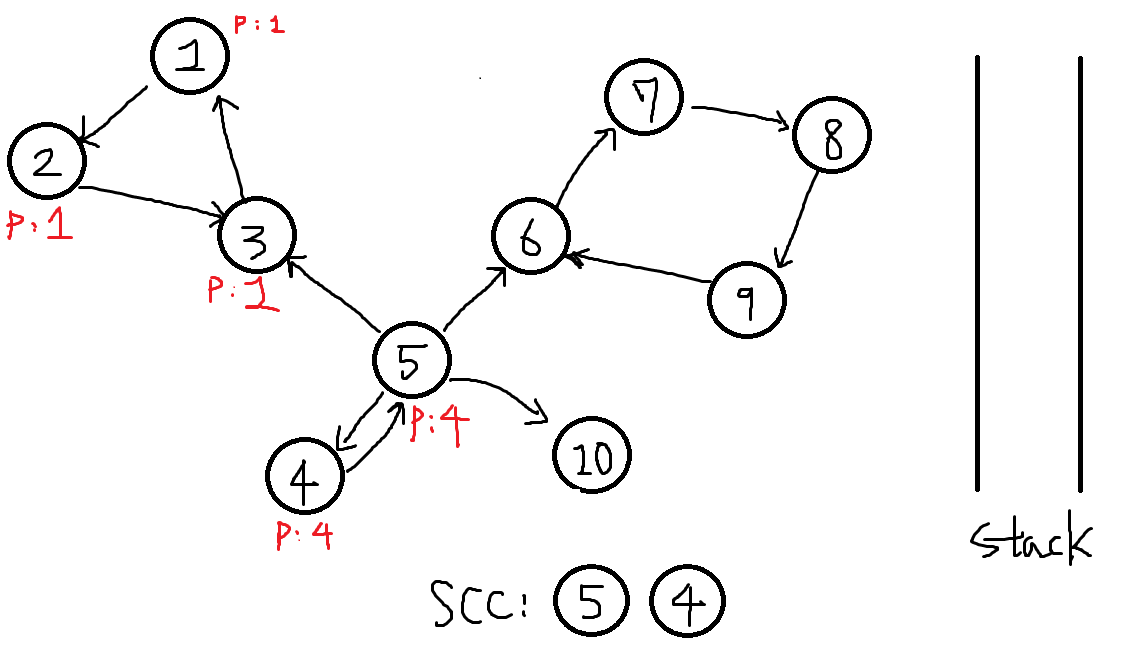    POP할때마다 뽑아낸 정점의 finished = true로 변환하는것을 잊지맙시다.

    추출한 scc를 저장합니다.

  10. 8번에서 도달가능했던 6번과 10번중 빠른 6번을 먼저탐색합니다.

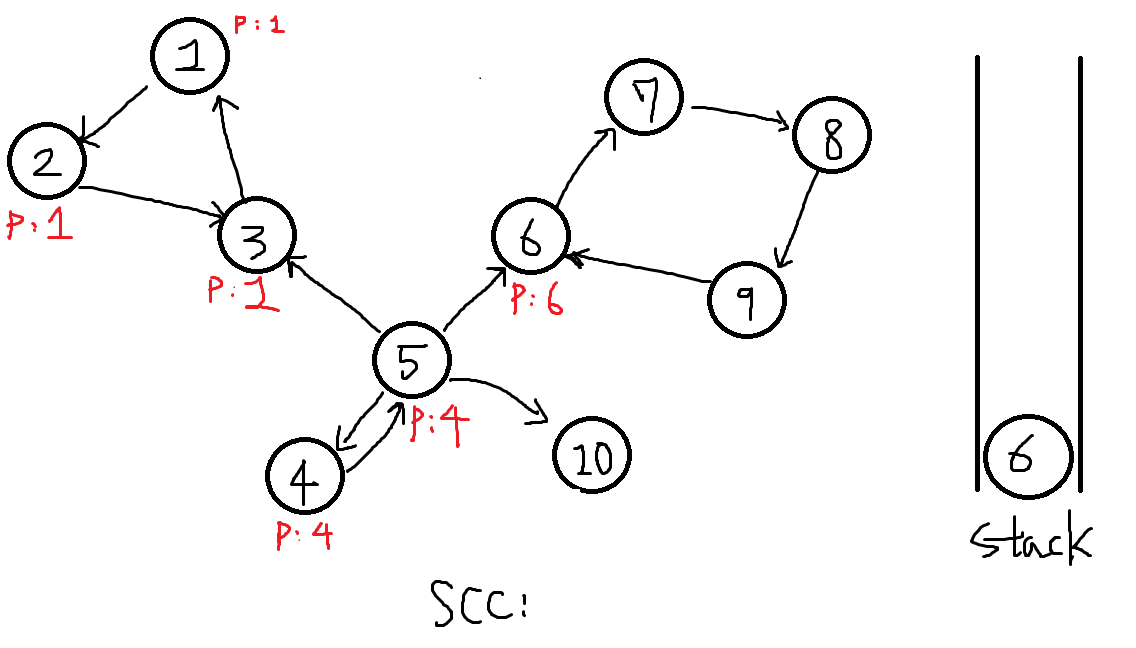
  11. 이어 7번을 탐색합니다.

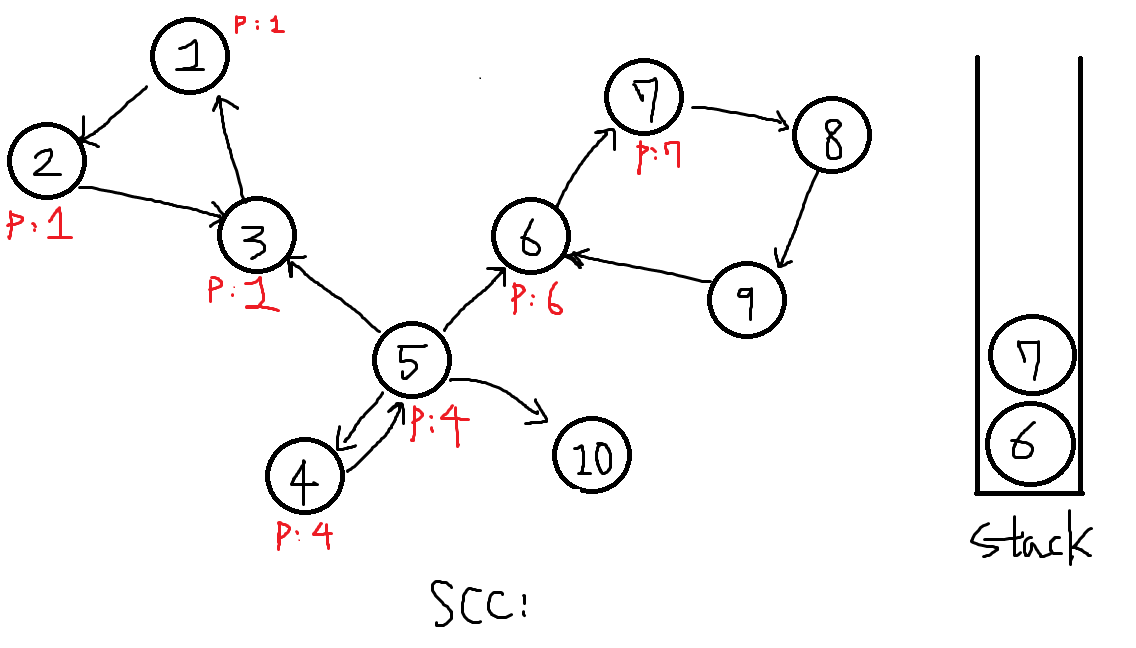
  12. 8번 탐색합니다.

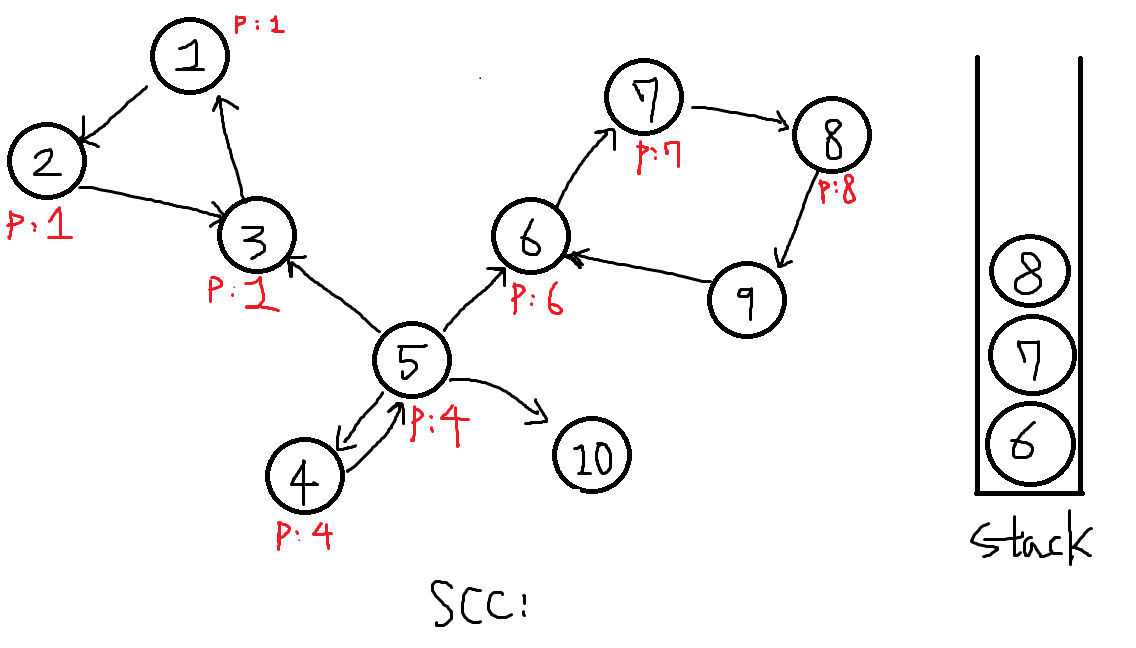
  13. 9번 탐색합니다.

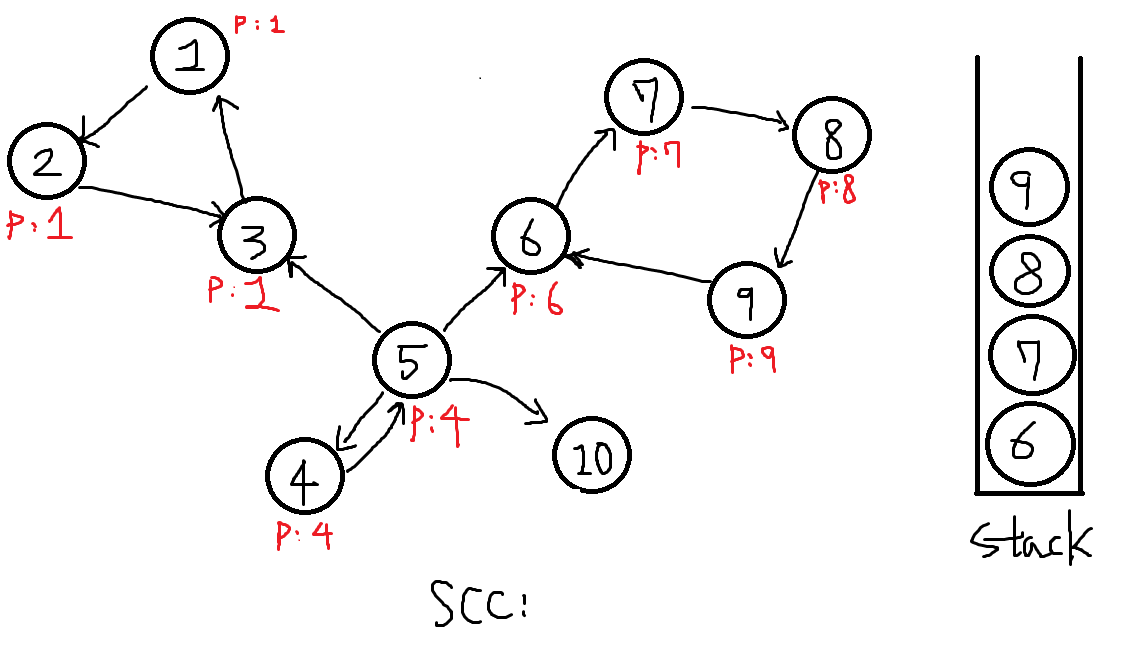
  14. 이어진 6번을 탐색하려는데 P[6] != 0입니다. 따라서 현재 정점의 부모를 P[6]으로 수정합니다. P[9] = P[6] = 6

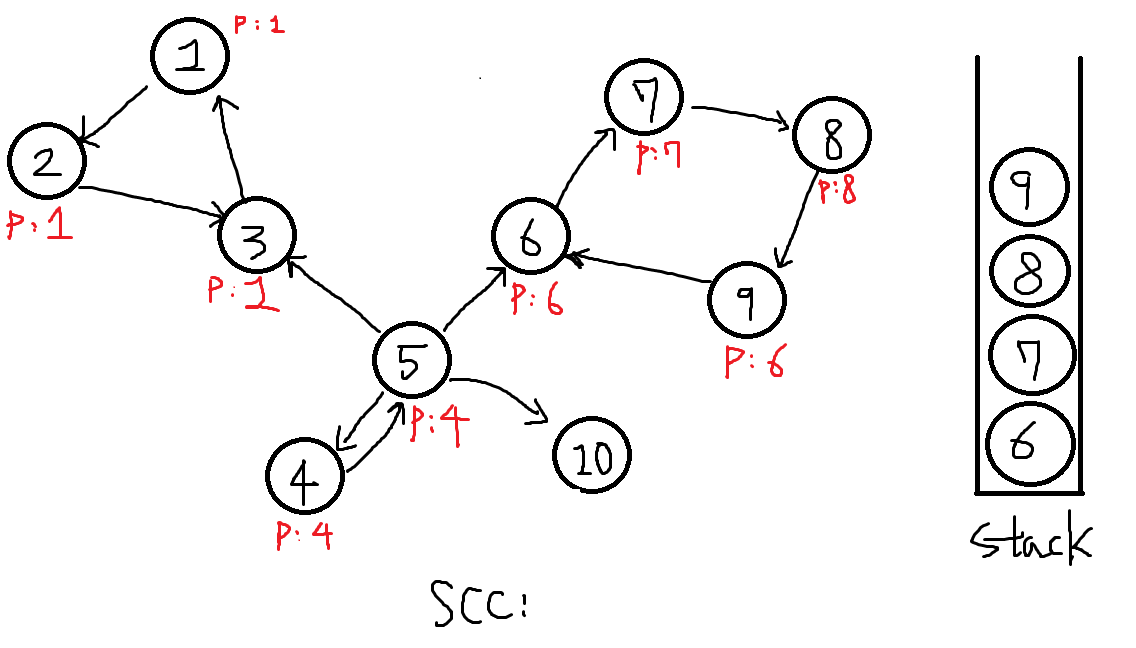
  15. 이젠 역순으로 8번을 탐색합니다. 8번의 다음이었던 9번이 P[9] != 0 이므로 8번의 부모로 P[9]를 지목합니다. P[8] = P[9] = 6

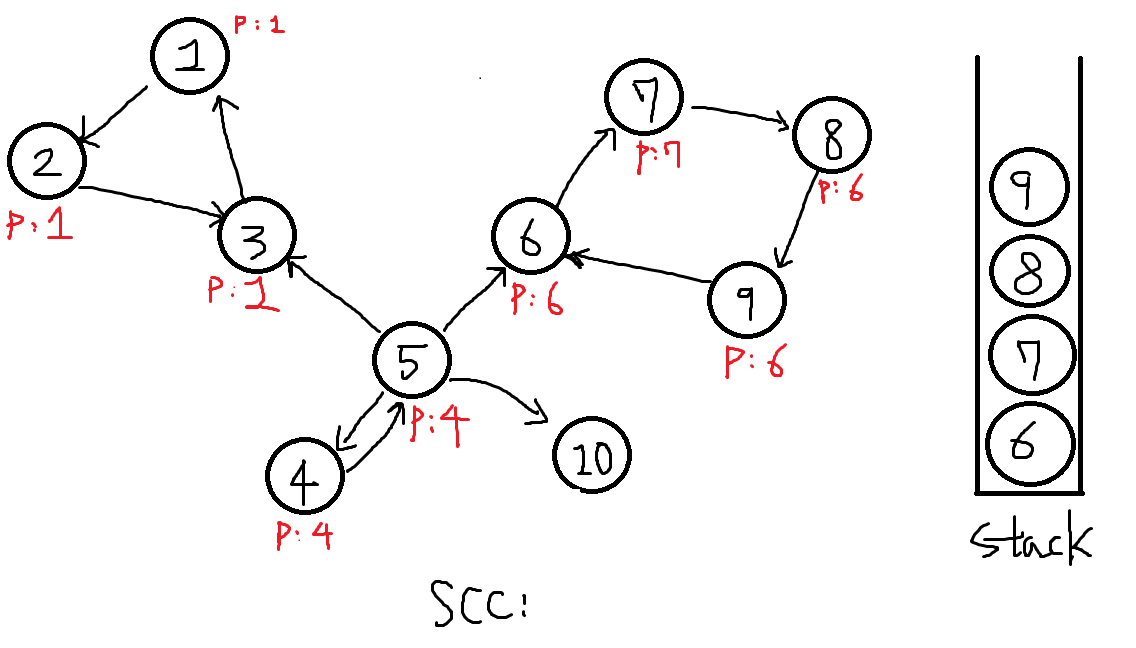
  16. 역순으로 7번을 탐색합니다. P[7] = P[8] = 6입니다.

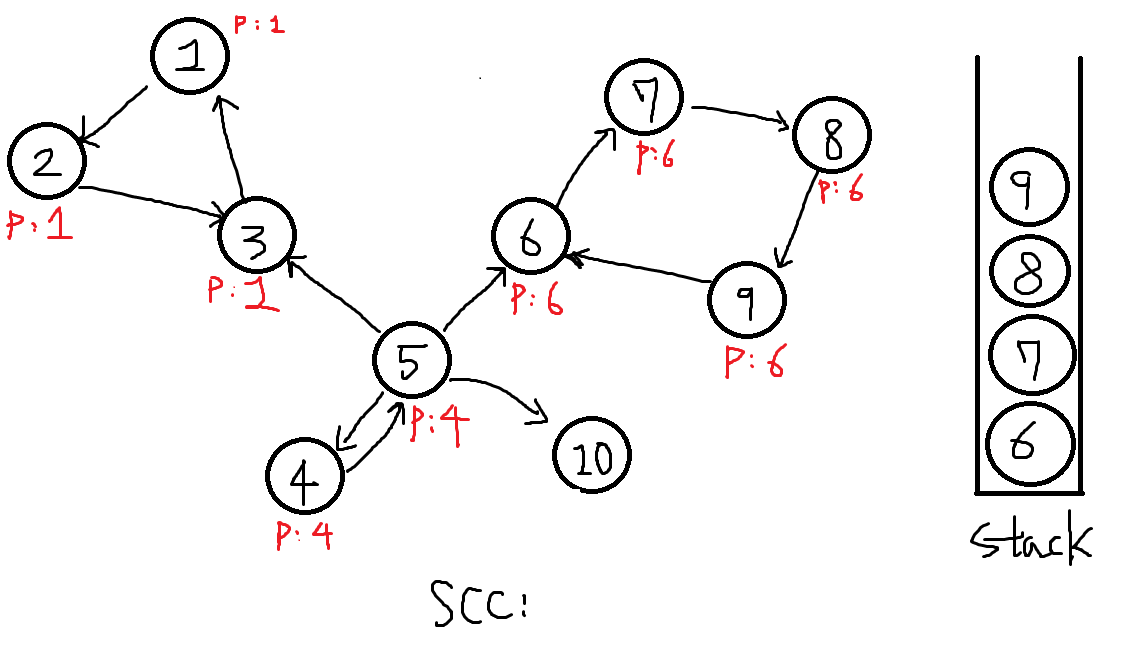
  17. 역순으로 6번을 탐색합니다. 이제 P[x] == x 인 점을 찾았습니다.
    이 또한 하나의 SCC를 찾은 것입니다.
    이제 6이 나올때 까지 스택에서 POP하며 finished를 체크합니다.

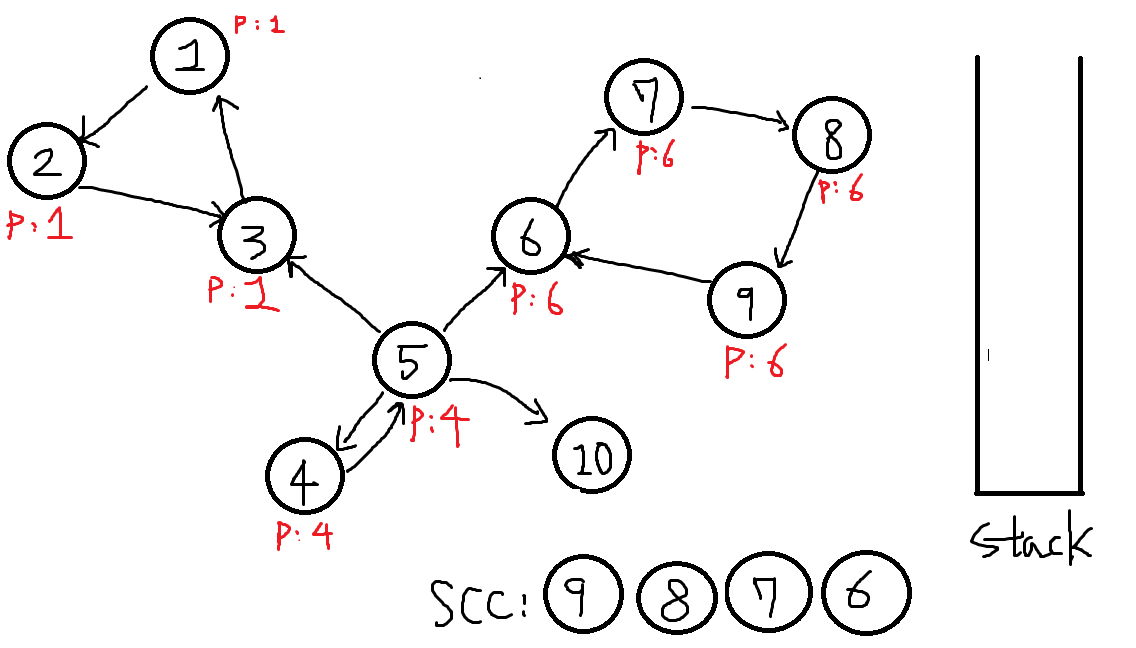
  18. 8번에서 마저 탐색하지 못한 10번을 탐색합니다.
    P[10] = 10, 스택에 넣습니다.

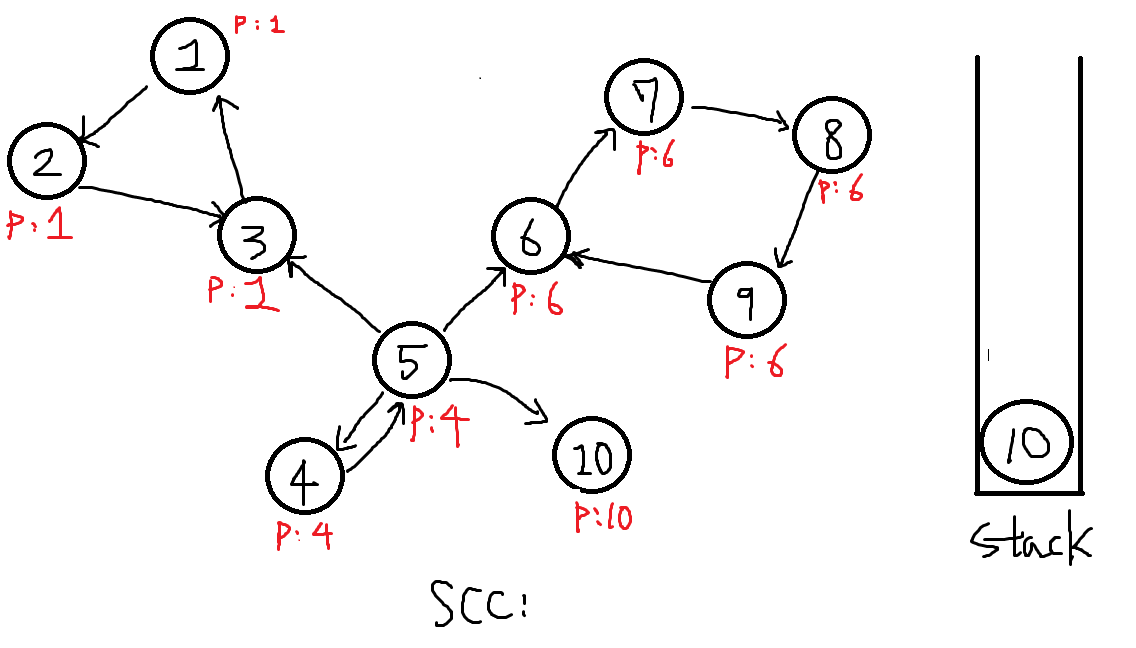
  19. 10에서는 더이상 도달가능한 정점이 없으므로 DFS를 수행하지 못하고 바로 P[x] == x 인지 체크합니다.
    결과는 P[10] == 10이므로 이또한 하나의 SCC로 분류됩니다.
    finished[10] = true.

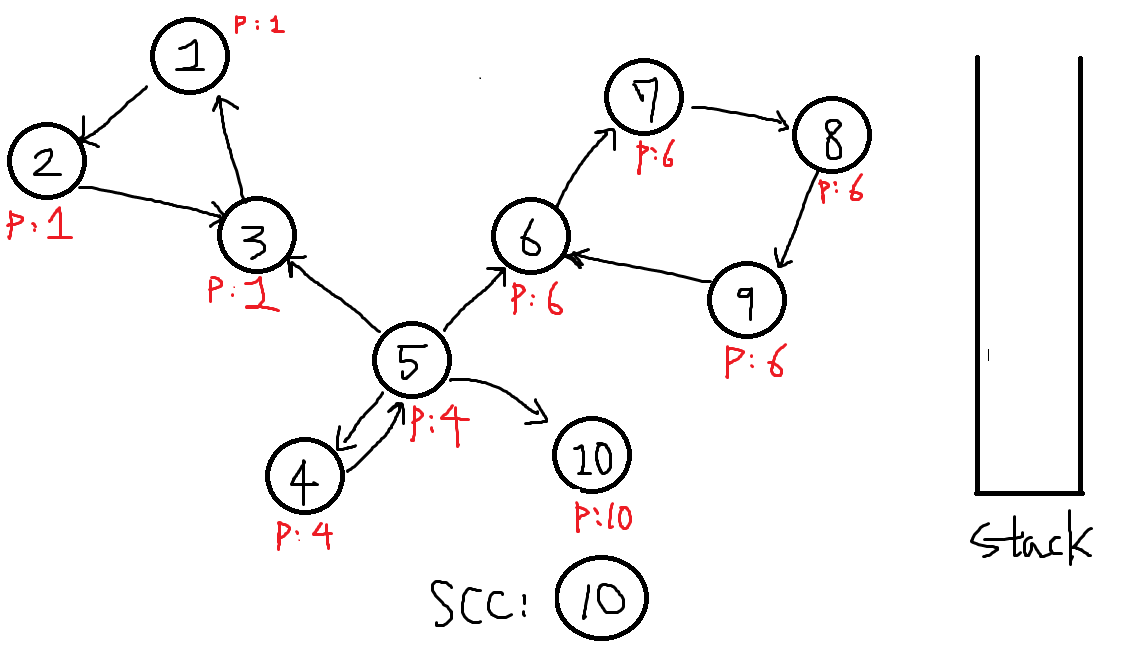
  20. 더이상 탐색할 정점이 없으므로 종료합니다.

번외 )) 만약 18번에서 10번과 이어진 또다른 정점 11번이 있었다고 칩시다. 그래프는 아래와 같습니다.

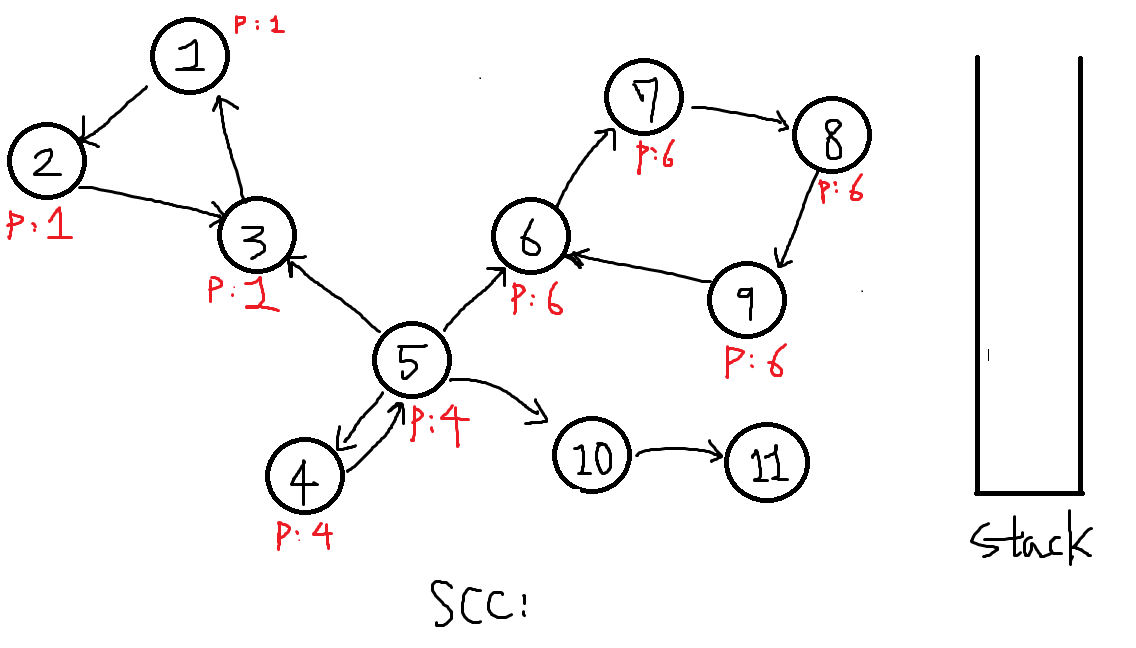
1. 여기서 10번정점부터 다시 탐색을 해봅시다.
P[10] = 10, 스택에 넣습니다.



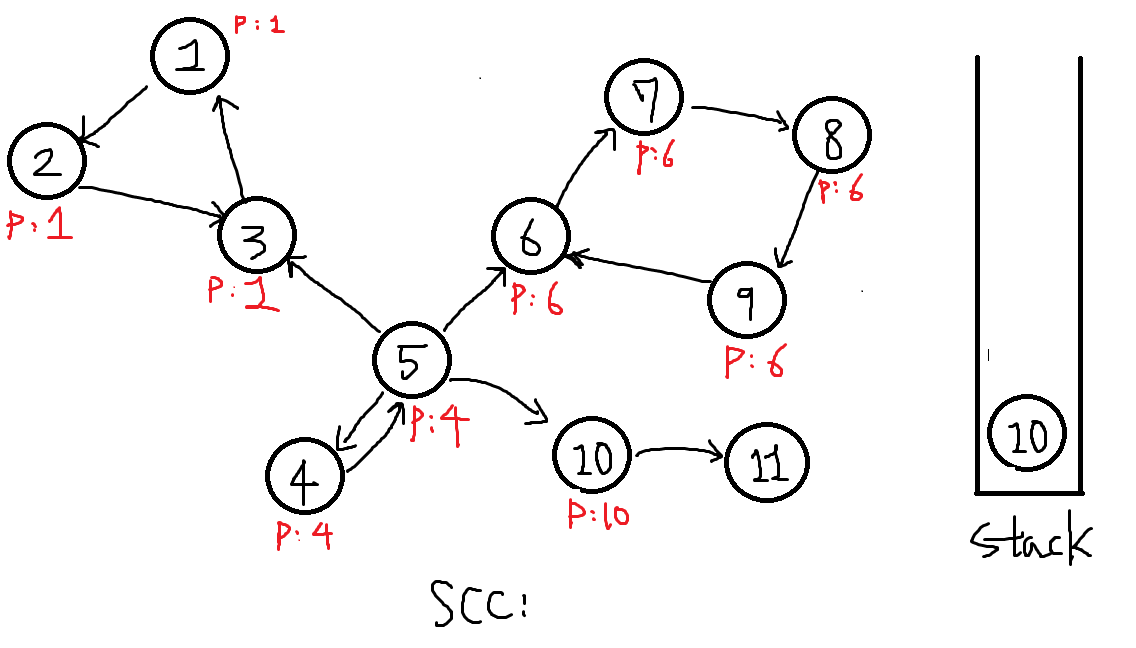
2. 이어진 정점 11이 있으니 DFS를 진행가능합니다. 11번을 탐색하여
P[11] = 11이고 스택에 넣습니다.

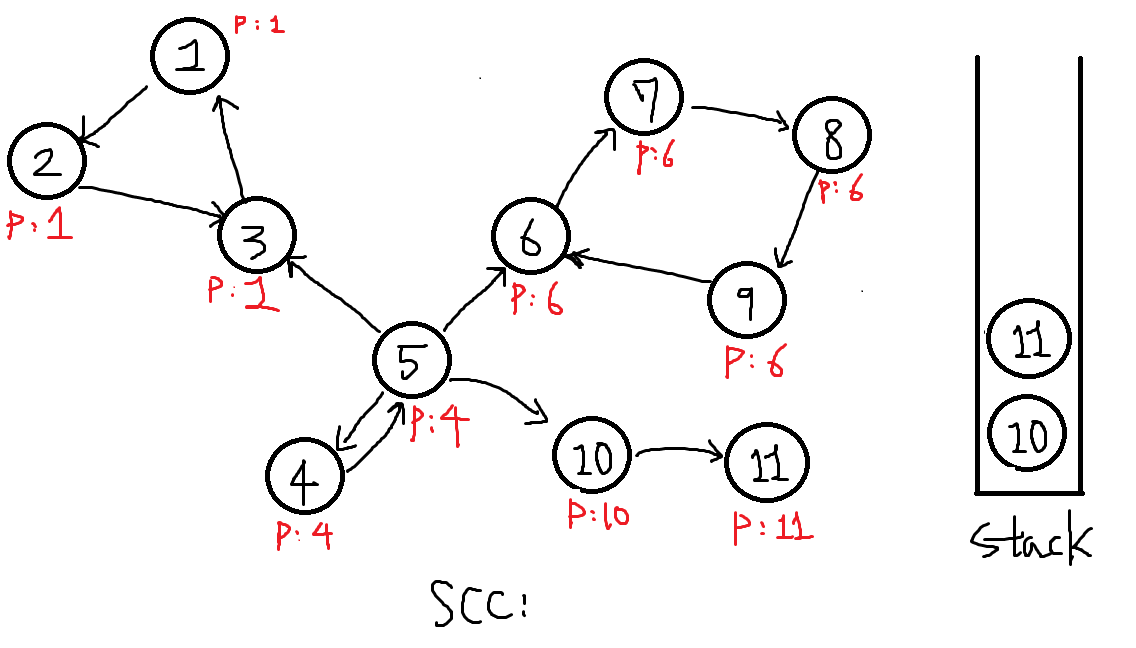
  1. 11에 이어진 정점이 이제 없으므로 DFS를 더이상 진행못합니다.
    이제 P[x] == x ? 확인결과 P[11] == 11 이므로 하나의 SCC를 찾은 것입니다.
    11번이 나올때까지 추출해서 SCC를 만들어봅시다.
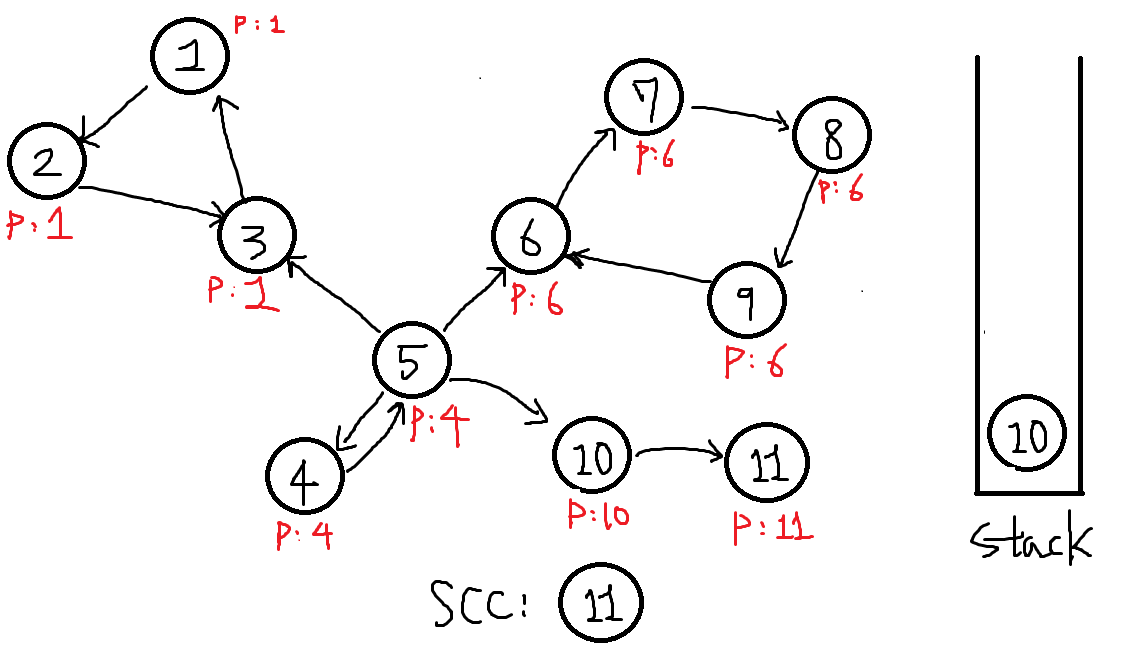    뽑음과 동시에 finished[11] = true입니다.

  2. 이제남은 10번으로 돌아갑니다. 2번으로 가능한 DFS를 모두 진행했으니 이젠 P[x] == x ? 확인할 차례입니다.
    P[10] == 10 이므로 이것도 하나의 SCC를 찾은것입니다.

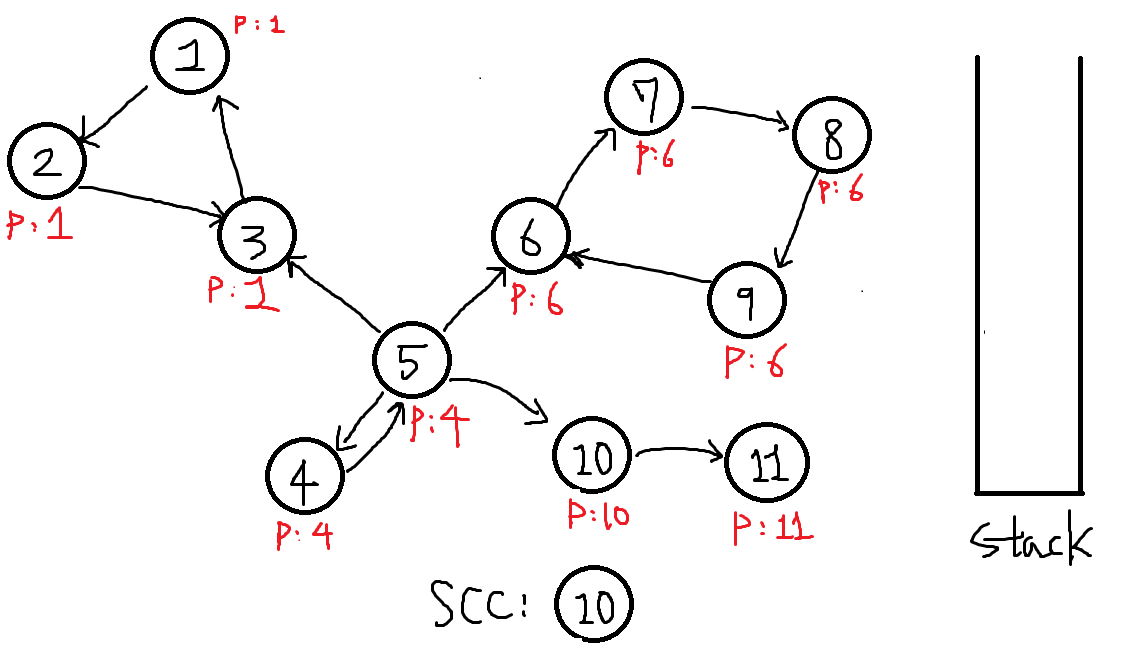
이렇게 사이클이없는 정점 10번, 11번과같은경우 각각이 하나의 SCC로 분류되며, 유향 그래프의 모든 정점은 여러 SCC로 모두 분류 될 수 있음이 확인되었습니다.!

또한 DFS를 진행하며 스택과 함께 재귀함수를 적용하므로, 10번에서 11번으로 DFS진행하다가 11번이 끝나면 다시 10번으로 와서 다음 단계인 P[x] == x인가? 를 진행하는것을 확인 했습니다.

타잔 알고리즘(DFS) 구현

사실상 SCC전체 코드입니다. 위에서 살펴본 모든 과정들이 녹아들어있습니다.

  1. 타잔 알고리즘을 이용한 DFS 구현이전에 필요한 요소들입니다. 그래프에대한 정보는 A벡터배열에 저장됩니다. A[1]에 정점1과 연결된 정점들 번호, A[N]에 정점N과 연결된 모든 정점들의 번호가 기록됩니다.
    또, 찾은 각각의 scc는 vector<vector<int>> SCC에 추가될 예정입니다.

  2. DFS코드
    설명 :
  • 91~92 : 필요한 모든 요소를 매개변수로 받았습니다. 이럴필요없이 int x로 현재 탐색중인 정점번호만 전달하고 나머지는 전역변수로 사용해도 됩니다.
  • 93 : 맨처음엔 자기자신을 부모노드P의 값으로 설정합니다.
  • 94 : 스택에 자기자신을 넣습니다.
  • 99~112 : 자신의 부모노드P를 DFS를 이용해 수정하는 과정입니다. 자세히 살펴보죠
  • 99 : 앞으로 찾은 부모노드번호는 parent에 기록할 예정.
  • 100 : 현재 정점과 연결된 모든 정점을 탐색할것입니다.
  • 101 : y는 연결된 다음 정점번호
  • 103 : 다음 정점y가 아직 DFS를 통해 방문하지 않았다면
  • 106 : 재귀적인 방법으로 방문하며, 그때의 값과 현재 parent값을 비교해 최솟값으로 parent를 갱신합니다.
    이 최소값으로 갱신하는 과정을 통해 하나의 SCC를 대표하는 부모노드값이 최소정점값이 되고, 우리는 DFS를 진행할때 가장낮은 정점부터 탐색하고, 심지어 스택에서도 가장 낮은 값이 맨아래에 존재할테니까
    갱신한 최솟값인 parent가 나올때까지 스택에서 POP을 해도 되는 조건이 완성됩니다.
  • 108 : 만약 DFS를 통해 방문했던 점이라면, SCC에 속한 정점인 지파악하는 finished를 확인합니다.
    SCC에 속하지 않았다면 현재 DFS과정을 통해 찾고있는 SCC그룹에 속한 정점이므로,
    이미 구해져있는 P[y] 값과 parent을 비교해 최솟값을 parent로 설정합니다.
  • 118 : 위에서 DFS를 통해 하나의 SCC를 그에 속하는 요소들중 최솟값인 정점번호로 P[x]를 모두 수정했으니 이를통해 스택에서 꺼내기위한 첫 단추입니다.
    재귀적구조로 이미 DFS(1), DFS(2), DFS(3), ...등 많이 호출되었으니 이중에서 해당 SCC를 대표하는 최솟값에 해당하는 DFS에서만
    스택에서 요소를 꺼내는 과정을 진행시키기 위한 조건입니다.
  • 119 : 스택에서 꺼낸 요소를 담기위한 벡터.
  • 120~126 : 스택에서 자기 자신의 값이 나올때 까지 POP하는 과정입니다. 자세히 살펴보죠.
  • 120 : while(1) { ... } 과 같습니다. x >= 1 이므로 무한 루프 시키기위함입니다.
  • 121~122 : 스택에서 요소를 꺼냅니다.
  • 123 : 꺼낸 요소를 벡터에 담습니다.
  • 124 : 꺼낸 요소를 앞으로 DFS에서 제외시키기위해 finished[x] = true로 설정해줍니다.
  • 125 : 자기 자신이 나오면 스택에서 꺼내는 행위를 멈춤니다.
  • 128 : 찾은 scc를 저장합니다.
  • 130 : DFS는 최종적으로 99~112에서 구한 parent 값을 리턴합니다.


    너무 설명이 길었지만, 그만큼 확실히 이해해야하는 과정이 많습니다.크게보면
    1번 : DFS로 하나의 SCC를 이루는 각각정점의 parent값을 최솟값으로 갱신하고
    2번 : 이후 DFS(x)의 parent==P[x]인 DFS(x)함수에서는 스택에서 요소를 꺼내어 하나의 scc로 만듭니다.
    3번 : 모든 DFS함수는 1번에서구한 parent값을 리턴합니다.
    이렇습니다.

아래는 DFS코드입니다.

#define MAX 10000
int id = 1, P[MAX]; //id: 정점번호, P: 
bool finished[MAX]; //SCC에 속한 정점 체크
vector<int> A[MAX]; //정점x와 인접한 정점들을 가지는 리스트
stack<int> S; //DFS에 사용될 스택
vector<vector<int>> SCC; //찾은 SCC들을 저장

//정점x에서부터 DFS를 진행해서 SCC를 찾는다.
//각 정점마다 한번씩 실행.
int findSCCusingDFS(int x, int& id, int (& P)[MAX], bool(&finished)[MAX],
	stack<int> &S, vector<int> (& A)[MAX], vector<vector<int>>& SCC) {
	P[x] = id++;
	S.push(x);

	//1. 정점x와 인접한 정점들의 부모노드를 결정
	//사이클이돌면(1-> 2-> 3-> 1 같은경우) 
	//findSCCusingDFS의 호출(1-1)을 멈추고 1-2번을 체크후 밑의 2번과정을 실행하게됨
	int parent = P[x];
	for (int i = 0; i < A[x].size(); i++) {
		int y = A[x][i]; //다음 요소
		//1-1. 아직 방문하지않은 정점X의 이웃정점들
		if (P[y] == 0)
			//ex) 1 -> 2 -> 3 까지 findSCC를 호출하면 각각 parent = 1, 1, 1로 고정되다가
			//3 -> 1 을 호출하면  P[x] != 0이니 아래 else if 로 넘어감
			parent = std::min(parent, findSCCusingDFS(y, id, P, finished, S, A, SCC)); 
		//1-2. 방문을 했으나 아직 SCC로 추출되지않은 정점X의 이웃정점들
		else if (!finished[y])
			//위에서 3 -> 1을 호출한상태면 아직 밑의 2번과정이 실행안되서
			//finished[1]=false이고 따라서 parent=1, P[y]=P[1]=1 인상태로 최솟값인 1이채택
			parent = std::min(parent, P[y]); 
	}
	//2. 찾은 부모노드가 자기자신인경우 SCC를 찾은것이니
	//자기자신이 나올떄까지 Stack 에서 POP
	//ex) 1 -> 2 -> 3 -> 1 인경우 위 1번과정에서 
	//findSCCusingDFS(1), findSCCusingDFS(2), findSCCusingDFS(3)을 실행했으나
	//이중에서 findSCCusingDFS(1)에서만 2번과정을 실행시키기 위한 조건이 parent == P[x]
	if (parent == P[x]) {  //부모정점에서만 SCC를 추출하는 2번과정을 실행시킨다.
		vector<int> scc;
		while (x) {
			int y = S.top(); 
			S.pop(); //스택에서 하나씩 POP
			scc.push_back(y); //뽑은 정점을 하나의 scc로 추가
			finished[y] = true; //POP한 정점이 SCC에 속해있음을 체크
			if (y == x) break; //자기자신이 나오면 멈춤
		}
		std::sort(scc.begin(), scc.end()); //찾은 scc내 원소들 정렬
		SCC.push_back(scc); //찾은 scc를 저장
	}
	return parent;
}

SCC 사용(전체 코드)

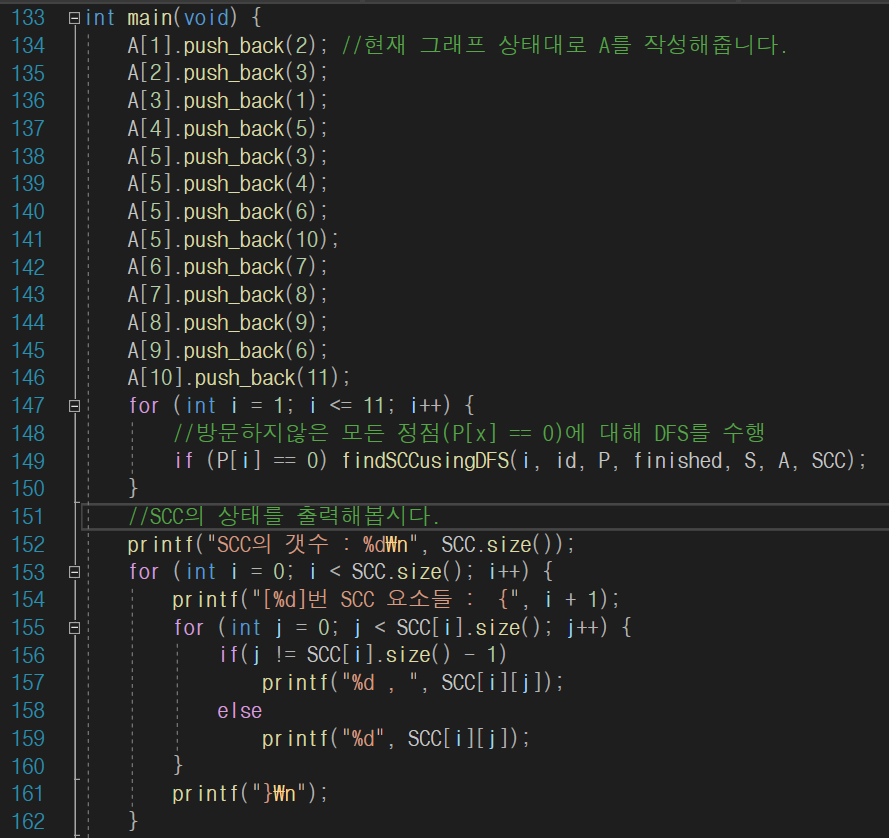
위에서 타잔 알고리즘을 DFS로 구현했으면 간단합니다.
방문하지 않은 모든정점에대해 1번부터 순차적으로 DFS를 실행시켜주면 됩니다.

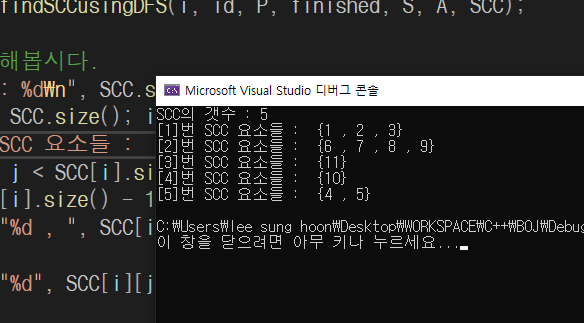실제 출력해본결과 잘 분류된 모습입니다.

아래는 전체 코드입니다.

#include <iostram>
#include<vector>
#include<stack>
#define MAX 10000
int id = 1, P[MAX]; //id: 정점번호, P: 
bool finished[MAX]; //SCC에 속한 정점 체크
vector<int> A[MAX]; //정점x와 인접한 정점들을 가지는 리스트
stack<int> S; //DFS에 사용될 스택
vector<vector<int>> SCC; //찾은 SCC들을 저장

//정점x에서부터 DFS를 진행해서 SCC를 찾는다.
//각 정점마다 한번씩 실행.
int findSCCusingDFS(int x, int& id, int (& P)[MAX], bool(&finished)[MAX],
	stack<int> &S, vector<int> (& A)[MAX], vector<vector<int>>& SCC) {
	P[x] = id++;
	S.push(x);

	//1. 정점x와 인접한 정점들의 부모노드를 결정
	//사이클이돌면(1-> 2-> 3-> 1 같은경우) 
	//findSCCusingDFS의 호출(1-1)을 멈추고 1-2번을 체크후 밑의 2번과정을 실행하게됨
	int parent = P[x];
	for (int i = 0; i < A[x].size(); i++) {
		int y = A[x][i]; //다음 요소
		//1-1. 아직 방문하지않은 정점X의 이웃정점들
		if (P[y] == 0)
			//ex) 1 -> 2 -> 3 까지 findSCC를 호출하면 각각 parent = 1, 1, 1로 고정되다가
			//3 -> 1 을 호출하면  P[x] != 0이니 아래 else if 로 넘어감
			parent = std::min(parent, findSCCusingDFS(y, id, P, finished, S, A, SCC)); 
		//1-2. 방문을 했으나 아직 SCC로 추출되지않은 정점X의 이웃정점들
		else if (!finished[y])
			//위에서 3 -> 1을 호출한상태면 아직 밑의 2번과정이 실행안되서
			//finished[1]=false이고 따라서 parent=1, P[y]=P[1]=1 인상태로 최솟값인 1이채택
			parent = std::min(parent, P[y]); 
	}
	//2. 찾은 부모노드가 자기자신인경우 SCC를 찾은것이니
	//자기자신이 나올떄까지 Stack 에서 POP
	//ex) 1 -> 2 -> 3 -> 1 인경우 위 1번과정에서 
	//findSCCusingDFS(1), findSCCusingDFS(2), findSCCusingDFS(3)을 실행했으나
	//이중에서 findSCCusingDFS(1)에서만 2번과정을 실행시키기 위한 조건이 parent == P[x]
	if (parent == P[x]) {  //부모정점에서만 SCC를 추출하는 2번과정을 실행시킨다.
		vector<int> scc;
		while (x) {
			int y = S.top(); 
			S.pop(); //스택에서 하나씩 POP
			scc.push_back(y); //뽑은 정점을 하나의 scc로 추가
			finished[y] = true; //POP한 정점이 SCC에 속해있음을 체크
			if (y == x) break; //자기자신이 나오면 멈춤
		}
		std::sort(scc.begin(), scc.end()); //찾은 scc내 원소들 정렬
		SCC.push_back(scc); //찾은 scc를 저장
	}
	return parent;
}

int main(void) {
	A[1].push_back(2); //현재 그래프 상태대로 A를 작성해줍니다.
	A[2].push_back(3);
	A[3].push_back(1);
	A[4].push_back(5);
	A[5].push_back(3);
	A[5].push_back(4);
	A[5].push_back(6);
	A[5].push_back(10);
	A[6].push_back(7);
	A[7].push_back(8);
	A[8].push_back(9);
	A[9].push_back(6);
	A[10].push_back(11);
	for (int i = 1; i <= 11; i++) {
		//방문하지않은 모든 정점(P[x] == 0)에 대해 DFS를 수행
		if (P[i] == 0) findSCCusingDFS(i, id, P, finished, S, A, SCC);
	}
	//SCC의 상태를 출력해봅시다.
	printf("SCC의 갯수 : %d\n", SCC.size());
	for (int i = 0; i < SCC.size(); i++) {
		printf("[%d]번 SCC 요소들 :  {", i + 1);
		for (int j = 0; j < SCC[i].size(); j++) {
			if(j != SCC[i].size() - 1)
				printf("%d , ", SCC[i][j]);
			else
				printf("%d", SCC[i][j]);
		}
		printf("}\n"); 
	}

	return 0;
}

여담

위 코드에서 int id=0으로 선언한뒤 DFS에서 P[x] = id++; 로 썼었는데, 보통은 int id;로 선언하고 P[x] = ++id; 사용한다고합니다. 이유는 시작정점번호가 1번으로 고정되있지 않을 수 도 있어서..
후자의 방법으로 id값을 설정하고 사용할 일이있으면 수정해서 사용하길 바랍니다.

관련 문제

https://www.acmicpc.net/problem/2150 >> https://velog.io/@cldhfleks2/2150
https://www.acmicpc.net/problem/4196 >> https://velog.io/@cldhfleks2/4196
https://www.acmicpc.net/problem/4013 >> https://velog.io/@cldhfleks2/4013
https://www.acmicpc.net/problem/6543 >> https://velog.io/@cldhfleks2/6543
https://www.acmicpc.net/problem/3977 >> https://velog.io/@cldhfleks2/3977
https://www.acmicpc.net/problem/11097 >> https://velog.io/@cldhfleks2/11097
https://www.acmicpc.net/problem/4305 >> https://velog.io/@cldhfleks2/4305

profile
이성훈
I will be a socially developer
이전 포스트

[Algorithm] Floyd-Warshall 플로이드-워샬

다음 포스트

[Algorithm] KMP, Knuth-Morris-Pratt 효율적인 문자열 탐색

0개의 댓글