개요

보통 문자열내에서 원하는 단어(부분문자열)를 찾고자 할때 2중 for문을통해서 찾는다. (단어가 한글자인경우 이진탐색이나 트라이 자료구조를 사용한다.)
하지만 이런 연산은 본문자열의길이와 찾는문자열의길이가 길어짐에따라 비효율적인
O(N * M)이 걸리는 연산이다.
이를 O(N + M)으로 개선 하기위해 고안된 알고리즘이 KMP(Knuth-Morris-Pratt)알고리즘이다.
사실 문자열이 문자들의 배열이기에 가능한 알고리즘으로, 이외에 수열에서도 대부분 같은 원리로 적용시킬 수 도 있다.

실패함수 작동원리

위에서 설명한 2중 for문으로 원하는 문자열을 찾는경우, 탐색에 실패한경우, 부분문자열의 처음위치(인덱스 0)에서부터 다시 탐색을 시작한다.
여기서 부분문자열의 맨처음이아니고, 그동안 일치했던 기록을 토대로, 특정인덱스까지만 되돌아가서
탐색을 이어나가면 어떨까? 해서 나온 알고리즘이다.
여기서 일치했던 기록을 실패함수, 배열로 구현된것을 실패테이블이라고 부른다.
이 실패 테이블을 만드는 과정을 그림으로 설명하겠다.


0. 먼저 찾고자하는 문자열내의 두 인덱스 i=1, j=0인 채로 시작하며 실패테이블인 1차원배열 F를 작성하는것을 목표로한다. 그림을 보면서 설명하겠다.
pattern[i] =?= pattern[j] 을 주로 확인하므로 빨간색카드 파란색카드가 서로 같은 pattern문자열임에도 두 인덱스 i, j가 마주보게 그린 모습이다.
여기서 두 카드에 F배열. 즉 실패 테이블 F를 같이 표현하였다.(두 카드의 F테이블도 같은것이다.)
1번을 가능한만큼 연달아 적용한다음 2번을 참이면 적용한다. 그리고 i를 +1하며 이어서 다시 1번 조건부터 확인하는 과정을 겪을 것이다.
이제 한단계 씩 살펴보자.


1. i == 1 ; 1번False 2번True
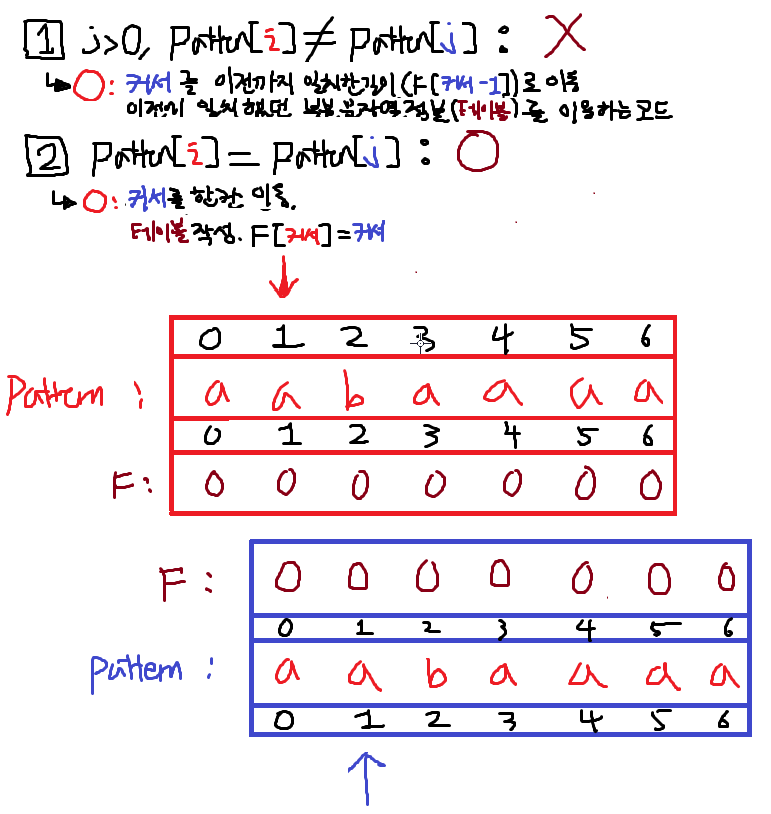F[i] = ++j 이므로 j(파란색커서)를 +1 한뒤
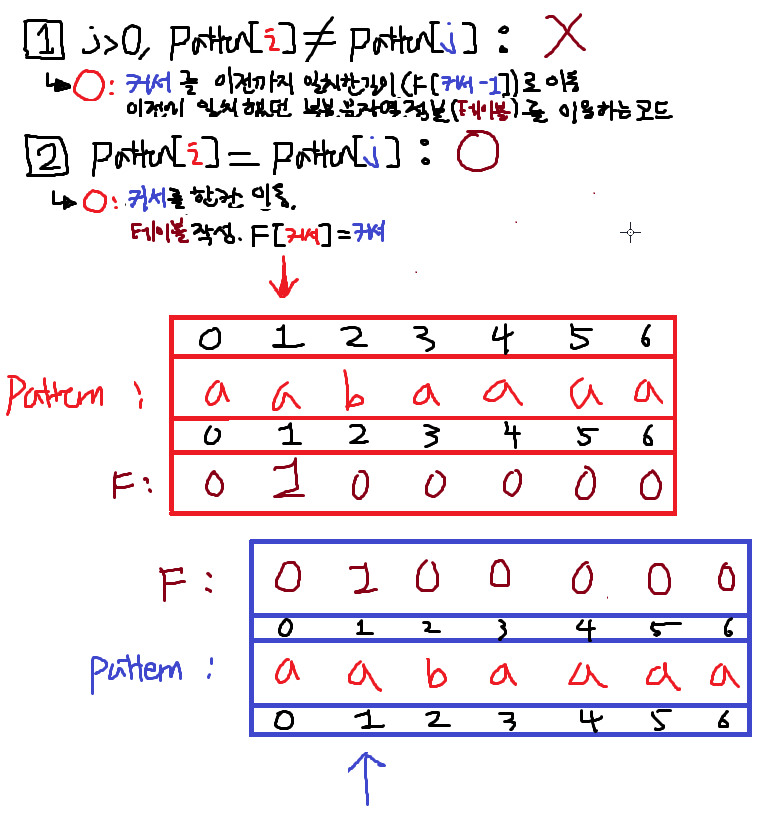F테이블에 그값을 적는다.



2. i == 2; 1번True
j되돌린다. F[j-1]의 위치는 갈색박스영역의 값이다.
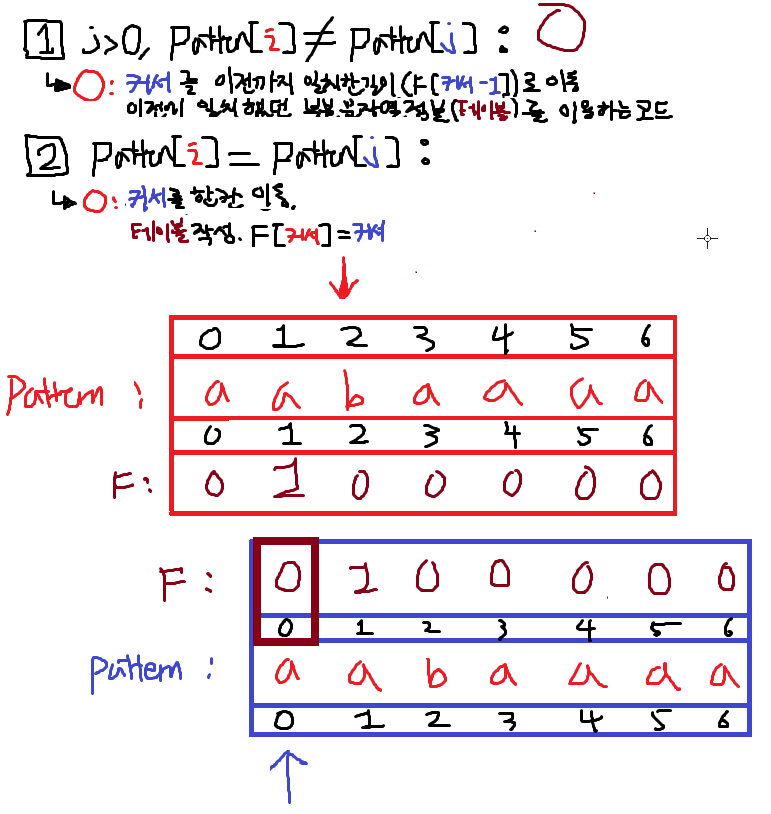이 값으로 j를 수정한다.


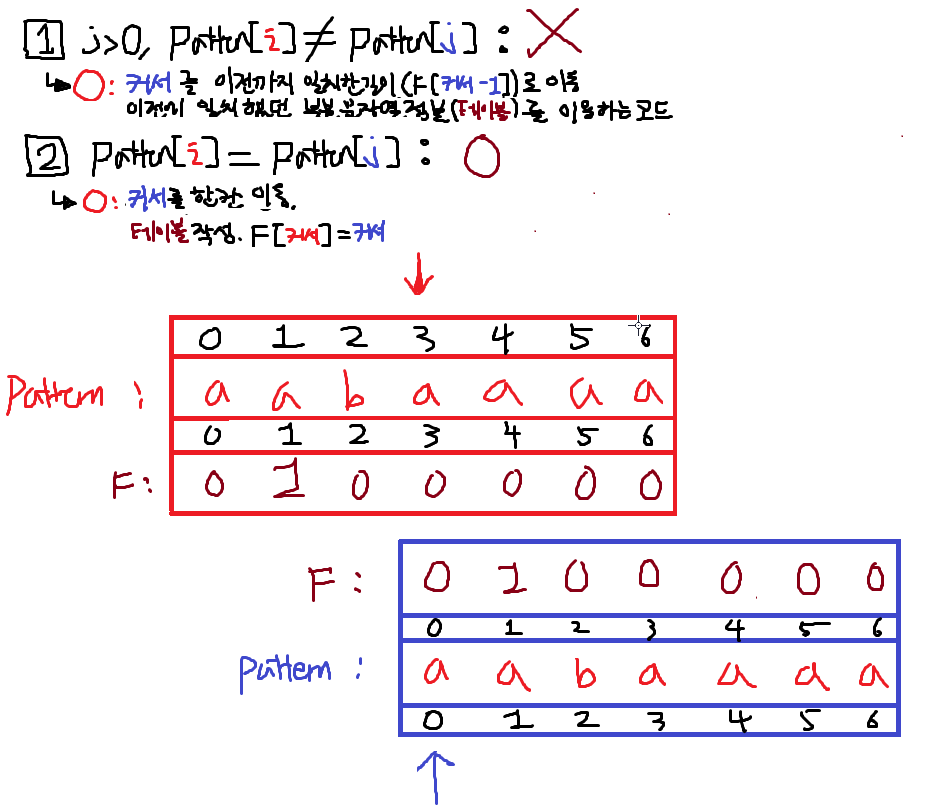
3. i == 2; 2번False
j를 변함이 없다.


4. i == 3; 1번False 2번True
j를 +1 한뒤 F테이블에 값을 적는다.



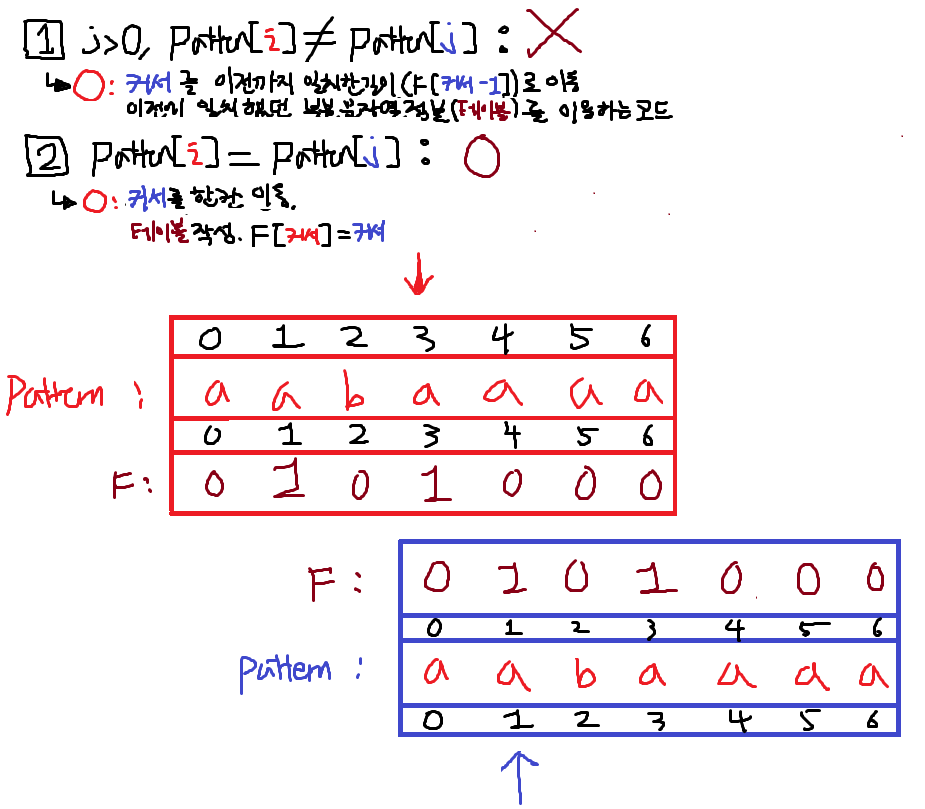
5. i == 4; 1번False 2번True
똑같다. j를 + 1, F[i] = j.



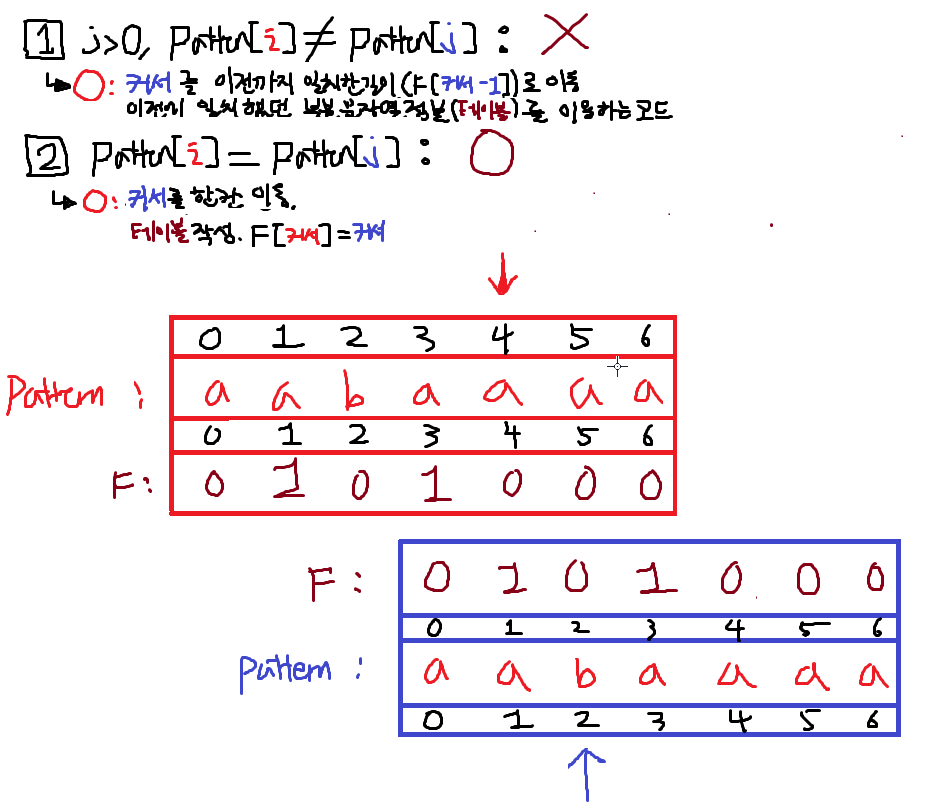
6. i == 5; 1번True
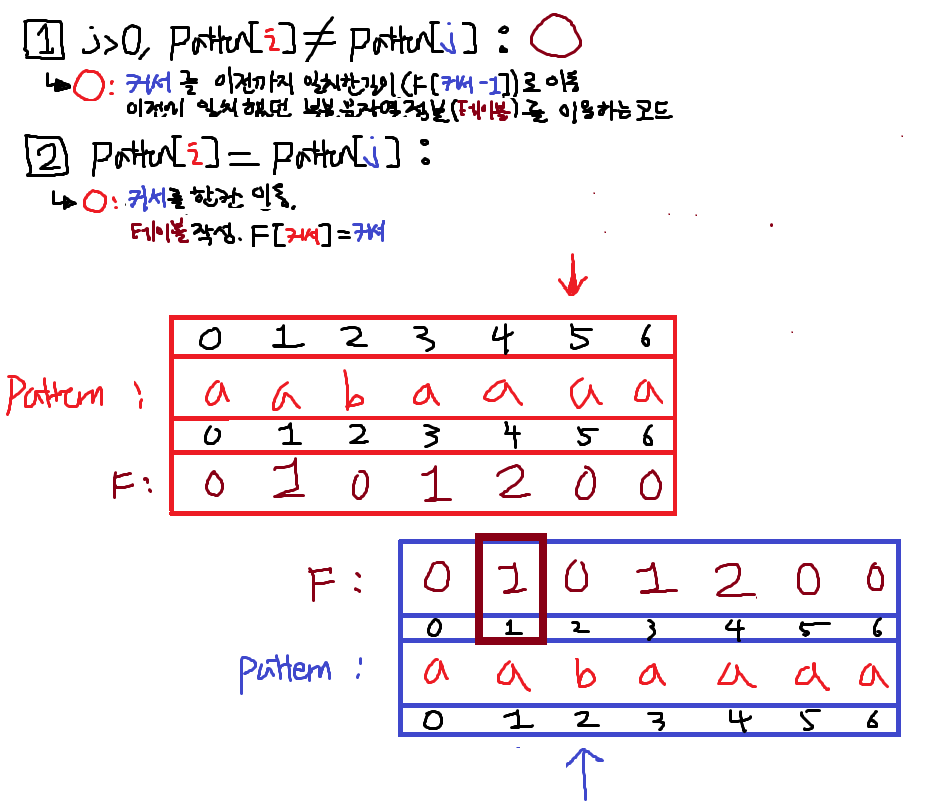j를 되돌린다. 갈색박스값이 F[j-1]의 값이다. 이것으로 j를 수정한다.
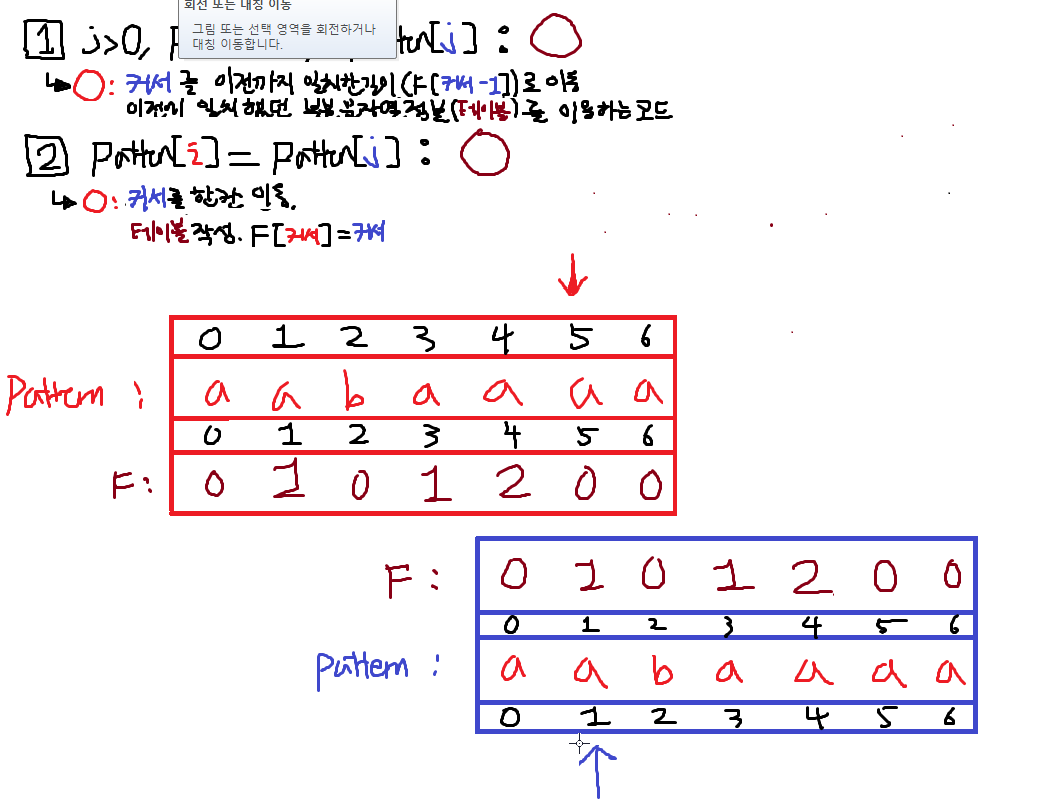이동하고나니까 2번조건이 True가 되었다.
따라서 j를 +1한뒤 실패테이블F[i]에 적는다.



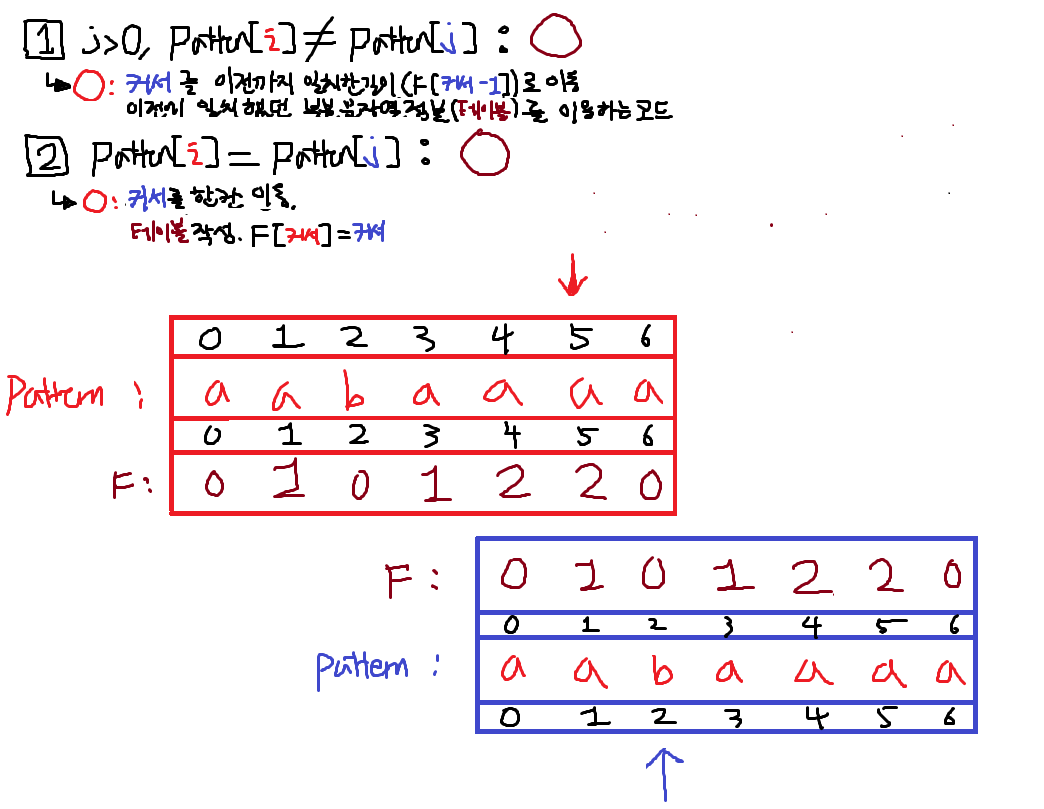
7. i == 6; 1번True
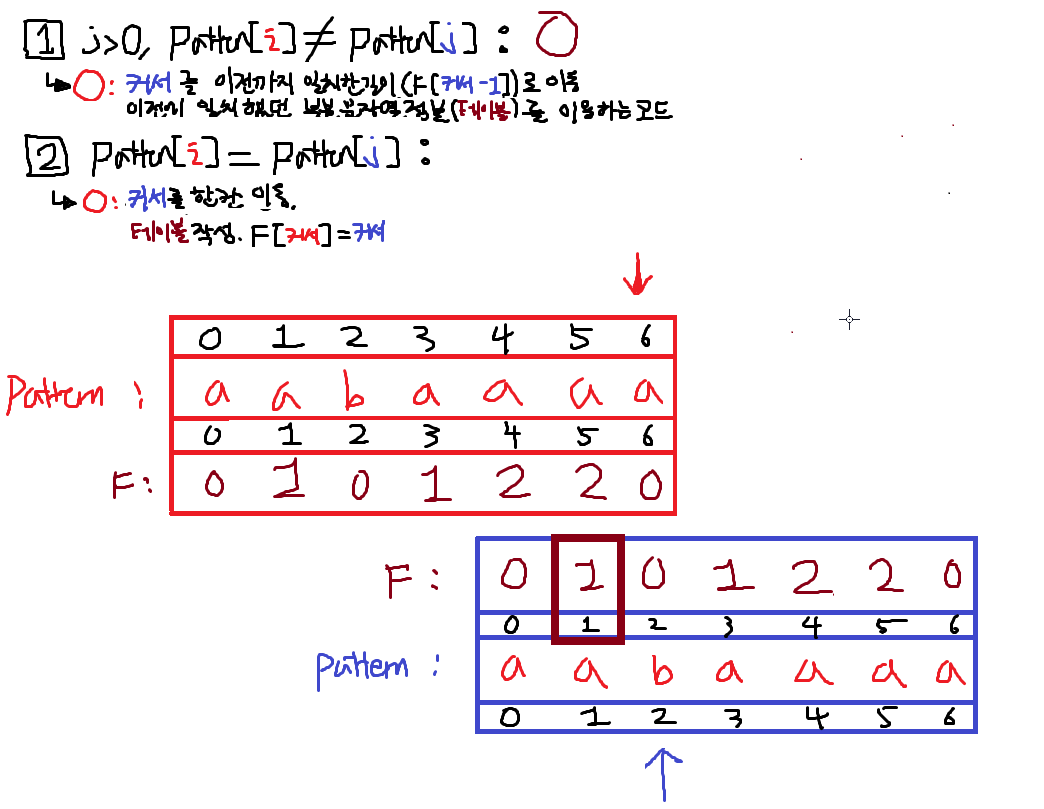이번에도 F[j-1]값을 갈색박스로 표시했다. j를 이 값으로 바꾼다면
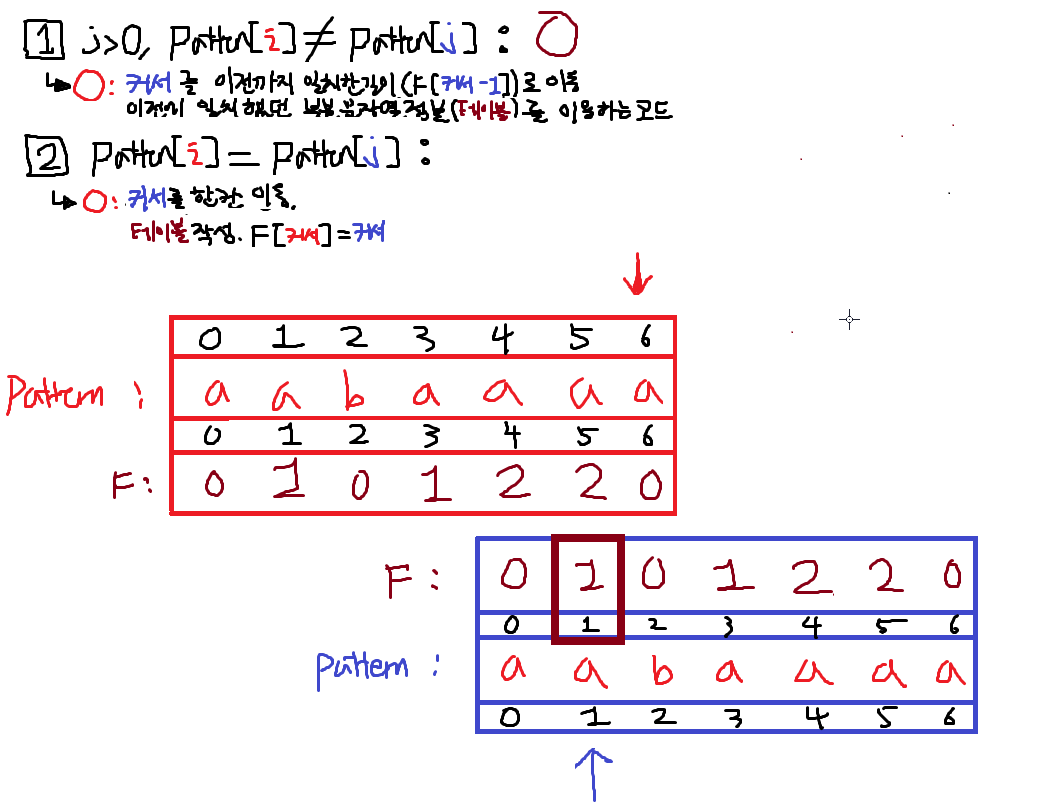이렇게될것이다. 이제 1번 조건이 False가 되었으므로 2번을 확인해보자.
2번조건이 True이므로 똑같이 j를 +1한뒤 F[i]에 적는다. 끝.




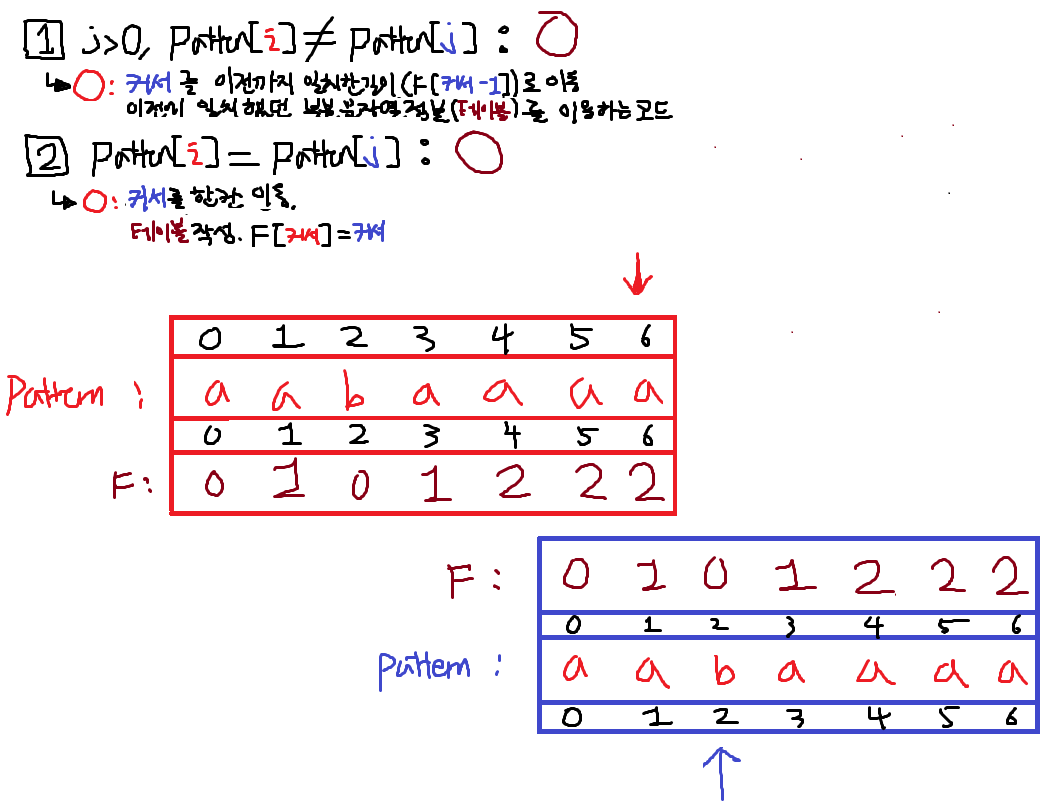이러면 실패테이블 F가 완성되었다.

이런식으로 실패테이블을 작성함과 동시에, 탐색에 실패할경우 while문을통해
작성하던 실패테이블을 역이용해서 재탐색위치를 효율적으로 찾아내어 결국 부분문자열에대한 실패 테이블을 완성시켰다.

왜 KMP알고리즘 이전에 부분문자열에대한 실패테이블을 먼저 설명하냐하면, 사실상 여기서 사용된 원리가 본문자열에서 부분문자열을 탐색하는과정에서 똑같이 쓰이기 때문이다.

실패함수 구현

코드를 본뒤에 설명을 하겠다.

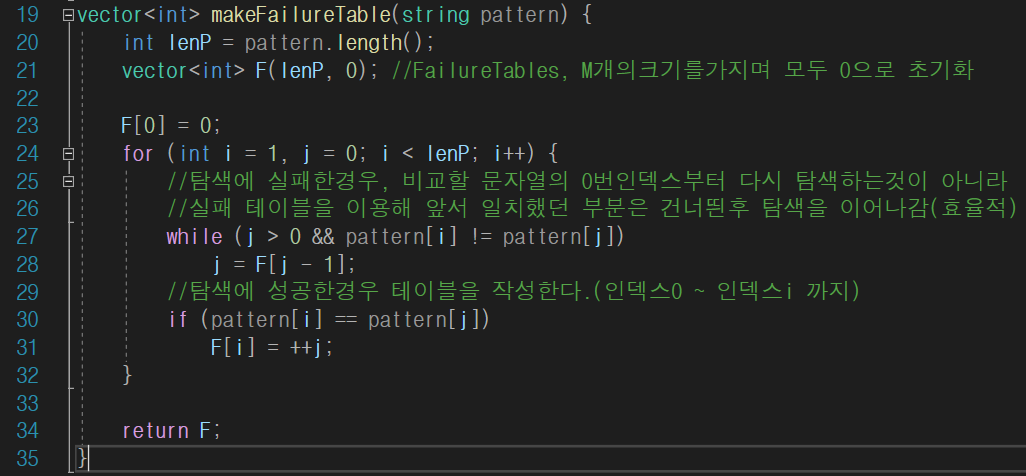
• line 24 : i=1, j=0에서 시작한다.
• line 27 : 앞서 그림에서본 1번과정이다. 여기서 while문을통해 건너띌 수 있는 최대인덱스까지 j를 수정한다. 따라서 작성된 테이블을 토대로 j의 위치를 확정시키는 부분이다.
• line 30 : j위치가 확정된후에, i와 j가 가리키는 문자를 확인한다.
  이때 둘이 같다면 실제로 테이블을 작성하는 부분이다.

막상 그림을 보다가 코드를 보면 사실상 2가지 조건만 확인하는 생각보다 간단하게 느껴진다.

아래는 실패함수 소스코드이다.

vector<int> makeFailureTable(string pattern) {
	int lenP = pattern.length();
	vector<int> F(lenP, 0); //FailureTables, M개의크기를가지며 모두 0으로 초기화

	F[0] = 0;
	for (int i = 1, j = 0; i < lenP; i++) {
		//탐색에 실패한경우, 비교할 문자열의 0번인덱스부터 다시 탐색하는것이 아니라
		//실패 테이블을 이용해 앞서 일치했던 부분은 건너띈후 탐색을 이어나감(효율적)
		while (j > 0 && pattern[i] != pattern[j])
			j = F[j - 1];
		//탐색에 성공한경우 테이블을 작성한다.(인덱스0 ~ 인덱스i 까지)
		if (pattern[i] == pattern[j])
			F[i] = ++j;
	}

	return F;
}

KMP 구현

사실상 위에서 구한 실패함수를 조금 손질하면 구현할 수 있다.
작동원리는 실패함수와 같으나 한가지 다른점은 실패테이블을 수정하지않고 활용만 한다는점이다. 코드를 보며 설명하겠다.

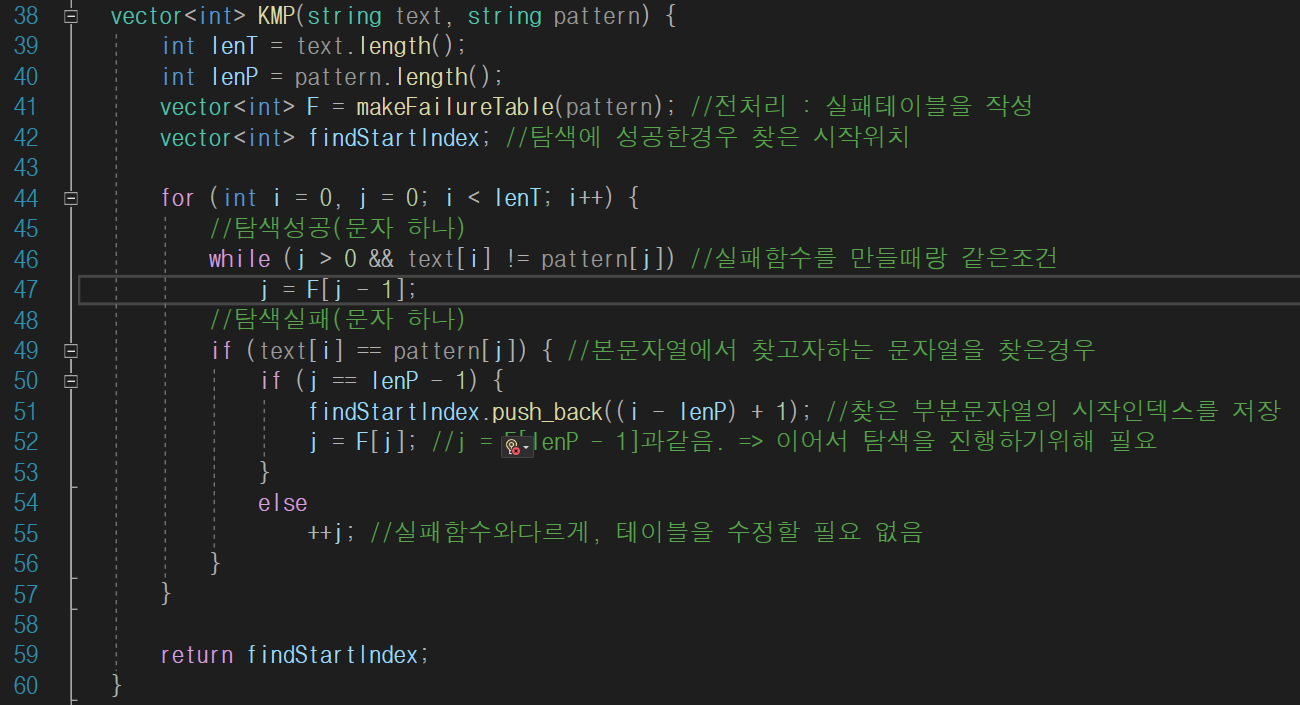
• line 46 : 실패함수의 1번과정과 같은부분이다. j가 적절한 위치를 찾아 되돌아가는 코드이다.
• line 49 : 실패함수의 2번과정과 같다.
• line 50 : 한가지 다른점으로, 찾고자하는 문자열을 찾았는가를 j가 찾는문자열의 끝부분일때로 정하였다.
  내부에 탐색을 성공한경우 할 작업을 지정해주면된다.
• line 52 : text에 pattern이 여럿존재하는경우 j를 다시 수정해주어야 정확하게 찾을 수 있다. 중요!!
• line 55 : i와 j가 가리키는 문자가 같으나, 문자열전체를 찾지않은경우는
  간단하게 j를 더해준다. 여기서 실패함수와 다른점이 실패테이블은 수정하지 않는다는점이다.

전체 코드

//1. 실패함수 : 실패테이블 작성하는 함수
//F[i] : 인덱스0 ~ 인덱스i까지의 접두사와 접미사가 일치하는 최대길이
vector<int> makeFailureTable(string pattern) {
	int lenP = pattern.length();
	vector<int> F(lenP, 0); //FailureTables, M개의크기를가지며 모두 0으로 초기화

	F[0] = 0;
	for (int i = 1, j = 0; i < lenP; i++) {
		//탐색에 실패한경우, 비교할 문자열의 0번인덱스부터 다시 탐색하는것이 아니라
		//실패 테이블을 이용해 앞서 일치했던 부분은 건너띈후 탐색을 이어나감(효율적)
		while (j > 0 && pattern[i] != pattern[j])
			j = F[j - 1];
		//탐색에 성공한경우 테이블을 작성한다.(인덱스0 ~ 인덱스i 까지)
		if (pattern[i] == pattern[j])
			F[i] = ++j;
	}

	return F;
}

//2. KMP : 실패테이블을 가지고 실제 문자열을 탐색한다.
vector<int> KMP(string text, string pattern) {
	int lenT = text.length();
	int lenP = pattern.length();
	vector<int> F = makeFailureTable(pattern); //전처리 : 실패테이블을 작성
	vector<int> findStartIndex; //탐색에 성공한경우 찾은 시작위치

	for (int i = 0, j = 0; i < lenT; i++) {
		//탐색성공(문자 하나)
		while (j > 0 && text[i] != pattern[j]) //실패함수를 만들때랑 같은조건
			j = F[j - 1];
		//탐색실패(문자 하나)
		if (text[i] == pattern[j]) { //본문자열에서 찾고자하는 문자열을 찾은경우
			if (j == lenP - 1)
				findStartIndex.push_back((i - lenP) + 1); //찾은 부분문자열의 시작인덱스를 저장
			else
				++j; //실패함수와다르게, 테이블을 수정할 필요 없음
		}
	}

	return findStartIndex;
}

관련 문제

https://www.acmicpc.net/problem/11585 >> https://velog.io/@cldhfleks2/11585
https://www.acmicpc.net/problem/1305 >> https://velog.io/@cldhfleks2/1305
https://www.acmicpc.net/problem/4354 >> https://velog.io/@cldhfleks2/4353
https://www.acmicpc.net/problem/1893 >> https://velog.io/@cldhfleks2/1893