개요

주어지는 2개의 문자열의 서로 공통인 부분수열중 길이가 가장 긴것의 길이를 찾는 알고리즘이다.
이때의 부분수열은 연속되지않은 부분수열도 포함하여 LCS를 찾게된다.
이번에 소개할 LCS알고리즘을 사용하면 두 문자열의 길이 N, M에따른
O(N * M)만에 LCS를 찾을 수 있다.

작동원리

LCS알고리즘을 설명할때 자주쓰이는 두 문자열 'ACAYKP', 'CAPCAK'로 설명하겠다. 두 문자열로 아래와 같은 테이블을 만든다.
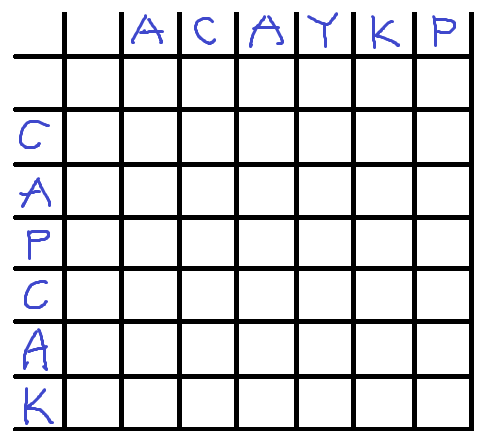테이블은 공집합인부분부터 각 문자열의 한글자씩해서 총 (N+1)*(M+1)칸으로 만드는데,
이 테이블이 dp[i][j]에 해당한다.
가장먼저 공집합간의 공통부분은 0 이므로 공집합을 포함한 칸은 모두 0으로 채운다.

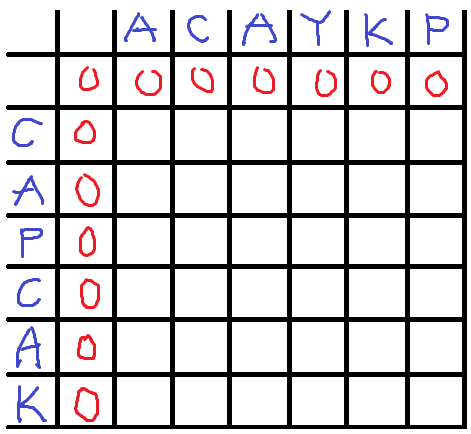
그다음 (1,1)부터 dp[i][j]를 아래의 두 규칙으로 채운다.
(두 문자열을 str1, str2로 설명하겠다.)

• str1 == str2 : 두 문자열의 각각 현재 문자가 같은경우
  공통된 부분의 갯수가 하나 늘어난것이므로, 현재문자 이전까지의 최장공통부분길이(dp[i-1][j-1]) + 1 이 현재 dp[i][j]가 된다.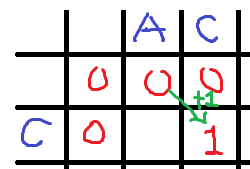 str1[1] == str2[0] 이므로 dp[1][2] = dp[0][1] + 1;
  
  
• str1 != str2 : 두 문자열의 현재 문자가 서로 다른 경우.
  위에서처럼 기존의 최댓값을 찾아서 dp테이블을 작성하면된다.
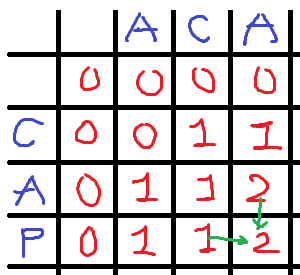  이때 기존의값은 두 문자열에서 현재문자를 하나씩 없앤 두 경우(dp[i-1][j] 와 dp[i][j-1])가 있을 수 있는데 이중 최댓값으로 dp[i][j]를 작성하면된다.

이처럼 기존의값을 참고하며 테이블을 작성해가므로 DP방법으로 풀리는 문제이다.

LCS 구현

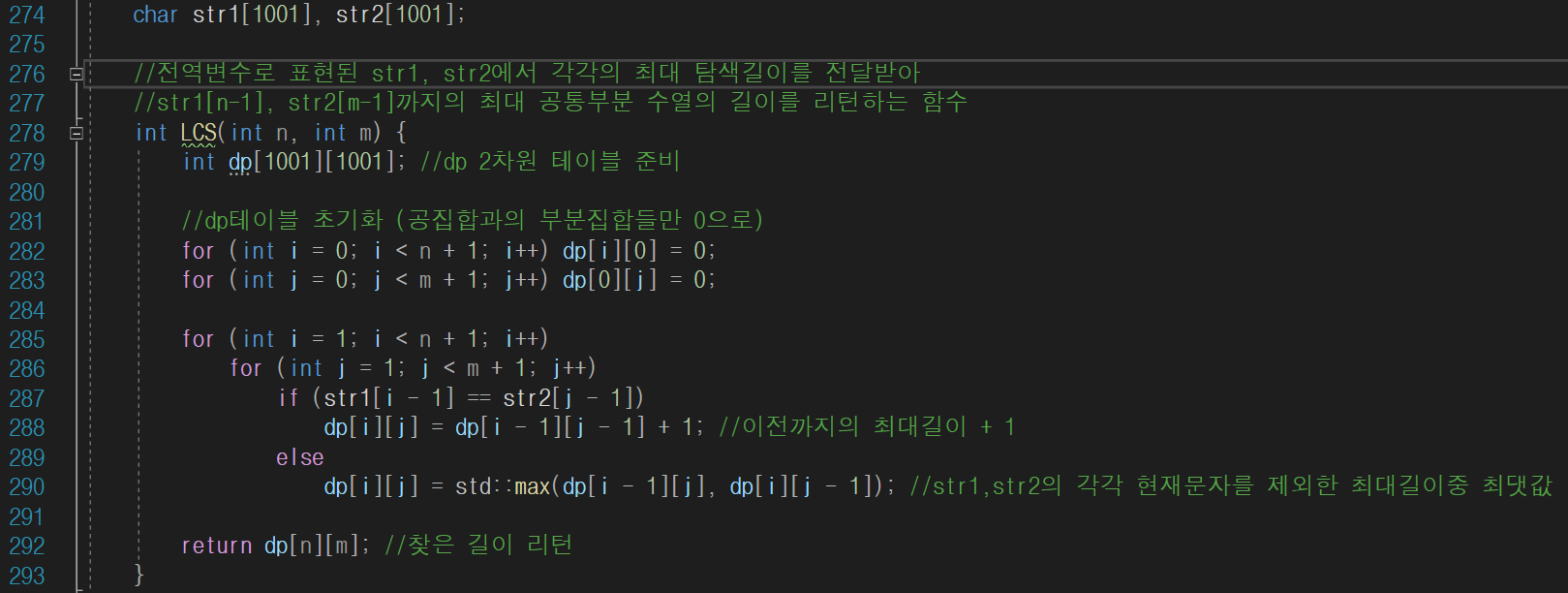
line 282,283 : 공집합과 비교되는 dp테이블의 칸은 모두 0으로 초기화한다.
line 285~290 : 문자열의 문자하나씩 비교하며 dp테이블을 작성하는 부분이다.

관련문제

https://www.acmicpc.net/problem/9251 >> https://velog.io/@cldhfleks2/9251