참고 : https://www.acmicpc.net/blog/view/9

개요

세그먼트트리는 배열 A가 있을때, 배열 원소를 업데이트하며 구간합을 구해야할때 사용한다.
세그먼트트리를 이용하지 않은경우, M번업데이트하는데 O(M), 구간합을 구하는데 O(N) 총 O(NM)의 시간복잡도가 걸린다.
이는 세그먼트트리를 이용할경우 업데이트, 구간합모두 O(logN)로 해결가능하다.
N = 5인경우의 세그먼트트리는 아래와 같다.

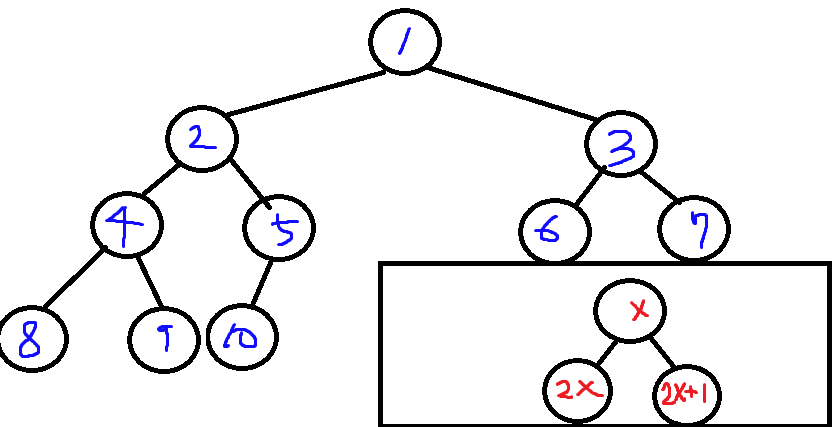
노드의 번호들이며, 오른쪽아래는 부모노드에서 자식노드로의 접근법이다.

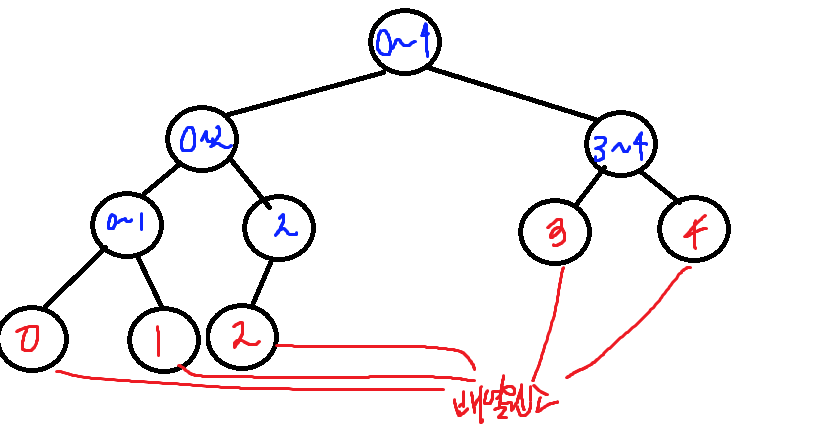
구간합을 나타내는 세그먼트트리

트리만들기

long long makeTree(vector<long long>& a, vector<long long>& tree, int node, int start, int end) {
	if (start == end) {
		return tree[node] = a[start];
	}
	else {
		return tree[node] = makeTree(a, tree, node * 2, start, (start + end) / 2) +
			makeTree(a, tree, node * 2 + 1, (start + end) / 2 + 1, end);
	}
}

• start == end : node가 리프노드인경우. 리프노드는 구간합이아닌 해당배열의 원소를 리턴해야함.
• node의 왼쪽자식은 node2, 오른쪽자식은 node2+1이다.따라서 왼쪽자식의 구간은 [start, (start+end)/2] 오른쪽자식은 [(start+end)/2+1, end]로 나눠지게된다.
• 재귀함수를 이용하여 왼쪽과 오른쪽자식 트리를 만들어 그합을 tree에 저장하게된다.

합 구하기

구간 left, right가 주어질때 구간합을 구하기 위해서는 루트부터 트리를 순회하며 각노드가 담당하는구간(start, end)과 left, right사이 관계를 주목해야한다.

1. [left, right] 와 [start, end] 가 겹치지 않는 경우
2. [left, right] 와 [start, end] 를 완전히 포함하는 경우
3. [start, end] 와 [left, right] 를 완전히 포함하는 경우
4. [left, right] 와 [start, end] 가 겹쳐져있는경우 (위 과정을 제외한 정상범주)

1번 : if (left > end || right < start) 이때는 탐색을 할 수 없으므로 탐색종료
2번 : if (left <= start && end <= right) 이때는 구할 합의 범위가 [left, right]인데 [start, end]와 그 노드의 자식도 모두 포함되기때문에 더이상의 호출은 비효율적
3번, 4번 : 왼쪽자식, 오른쪽자식을 루트로하는 트리에서 다시 탐색을 반복

long long sum(vector<long long>& tree, int node, int start, int end, int left, int right) {
	if (left > end || right < start) {
		return 0;
	}
	else if (left <= start && end <= right) {
		return tree[node];
	}
	else {
		return sum(tree, node * 2, start, (start + end) / 2, left, right) +
		sum(tree, node * 2 + 1, (start + end) / 2 + 1, end, left, right);
	}
}

배열 원소 업데이트

우리는 구간합을 구하는것이 세그먼트트리의 사용목적임을 아므로, 어떤원소가 얼마만큼 변했는가를 알아야한다. 이 수가 diff라면 diff = 변한값 - a[index] 으로 구할 수 있다.

1. [start, end]에 index가 포함된 경우
2. [start, end]에 index가 포함되지 않은 경우

node의 구간([start, end])에 포함되는경우 diff만큼 노드를 모두 증가시켜 변경해줄 수 있다.
tree[node] += diff.
하지만 포함되지 않은경우는 그 자식도 index를 포함하지 않으므로, 탐색을 종료한다.

void update(vector<long long>& tree, int node,
	int start, int end, int index, long long diff) {
	if (index  < start || index > end) return; //포함X 종료
	tree[node] += diff;
	//리프노드가 아닐때만 아래의 과정으로
	// 모든 자식의 구간합을 변경
	if (start != end) { 
		update(tree, node * 2, start, (start + end) / 2, index, diff);
		update(tree, node * 2 + 1, (start + end) / 2 + 1, end, diff);
	}
}

마지막으로, 세그먼트트리를 이용한 대표적인 백준사이트 문제풀이이다.
https://velog.io/@cldhfleks2/2042