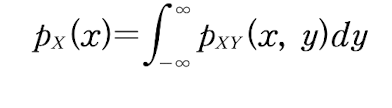[AI 기초] 확률

표본 공간

• 이산 표본 공간: 표본 공간을 구성하는 원소가 유한개
• 연속 표본 공간: 표본 공간을 구성하는 원소가 무한개

랜덤 변수(random variable)

X = X(e)는 표본 공간을 구성하는 각 원소(e)에 하나의 실숫값(real number)를 대응시키는 함수로 정의된다

랜덤 변수의 정의역(domain): 표본 공간
랜덤 변수의 치역(range): 전체 실수 영역

PDF, CDF

PDF(probabilty distribution function)
CDF(cumulative distribution function): 누적 분포 함수라고 부르며, 랜덤 변수 X가 x보다 작은 값을 가질 확률을 의미한다. 정의는 아래와 같다.

• CDF의 특징:
  - 단조증가함수
  • x->양의무한대이면 CDF = 1
  • x->음의무한대이면 CDF = 0
• PDF와 CDF의 관계
  

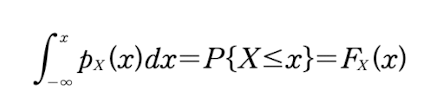
CDF가 미분이 가능하다면

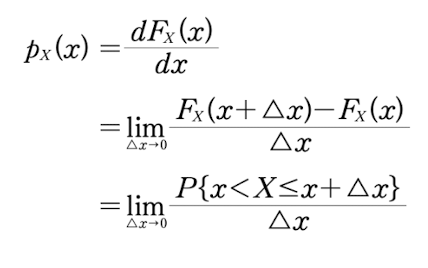
랜덤 변수 X가 어떤 실수 구간 (a, b]에 속할 확률을 CDF와 PDF를 이용해 나타내면

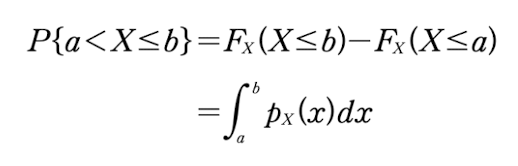
즉 (a, b] 구간의 PDF의 면적이 된다.

PMF

이산 표본 공간에서는 PDF 대신 PMF를 쓴다
PMF(Probability mass function)

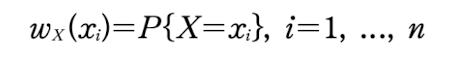
dirac delta 함수를 이용한 CDF 표현

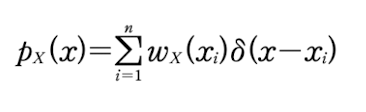
결합 확률 함수

랜덤 변수 X, Y의 결합 CDF는 다음과 같이 정의를 한다

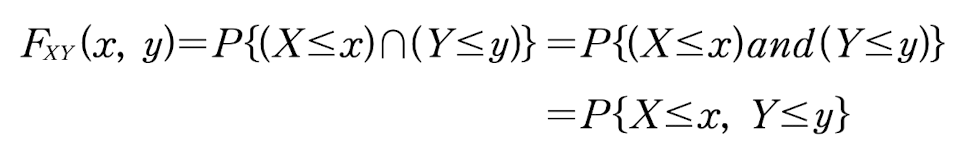
결합 CDF의 성질

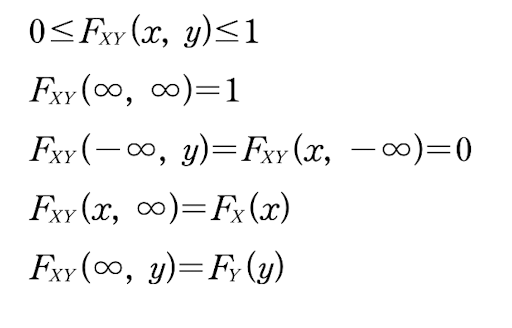
결합 CDF, PDF의 관계

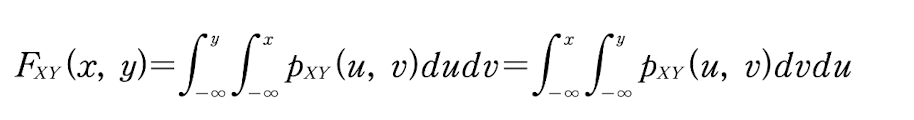
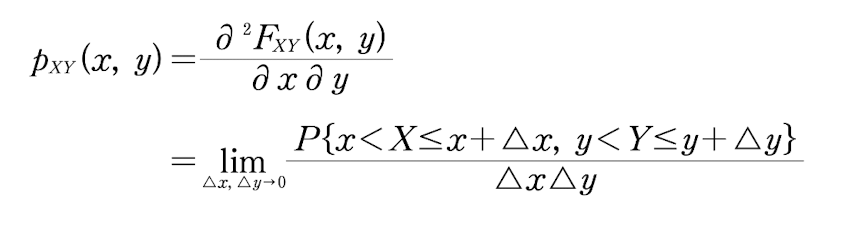
• marginal density function
  X, Y의 결합 PDF를 적분하여 X 또는 Y 중 하나에 대한 결합 PDF를 구할 수 있다.
  이를 Marginal Density Function, 한계 밀도 함수라고 한다.