본 포스트를 보기 전에 이전 포스트를 먼저 보시면 도움이 됩니다.
본 포스트를 작성하는데 아래 링크들의 내용을 참고하였습니다. 그리고 본 포스트에 사용되는 모든 이미지는 1번 링크에서 가져왔습니다.
1. Four Ways to Compute an Inverse FFT Using the Forward FFT Algorithm
2. DSP Tricks: Computing inverse FFTs using the forward FFT
3. FFT로 IFFT 변환하기 - (1): Time-Reversed/Complex Conjugated Input
Method-I
- FFT 입력 이전에 Time-Reversal을 적용
- FFT 이후 배 scaling
- 원리는 이전 포스트 참고
 * source: https://www.dsprelated.com/showarticle/800.php
* source: https://www.dsprelated.com/showarticle/800.php
Method-II
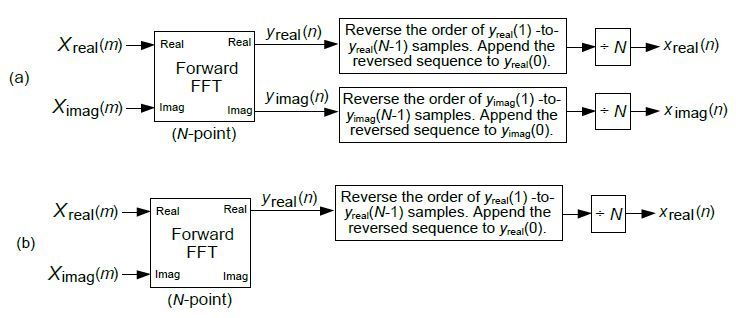
- Method-I에서는 입력 샘플에 time-reversal을 적용하였으나 method-II에서는 출력 샘플에 time-reversal 적용
- FFT와 IFFT가 서로 반대 방향으로 위상 회전을 측정하는 것이기 때문
- 자세한 내용은 이전 포스트 참고
- 만약 입력 샘플이 conugate symmetric하다면 아래 그림의 (b)번과 같이 real output에만 time-reversal을 적용하면 됨.
- 참고로 conjugated symmetry란, 입력 샘플이 을 만족하는 것을 의미 - 마지막으로 배 scaling
Method-III
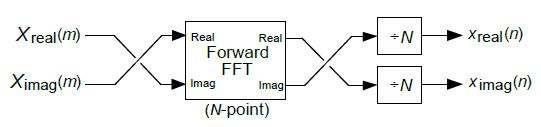
- 입력 샘플을 IQ swap 한 후 FFT 변환
- FFT 출력에 다시 IQ swap 적용
- 마지막으로 배 scaling
- 이런 연산이 가능한지 간략히 검토해보면, FFT와 IFFT의 weight 값은 서로 complex conjugate 관계이므로 입력이 IFFT weight 값이 라 할 때,
- No swap + IFFT:
- IQ swap + FFT:
- 따라서 IQ swap FFT IQ swap 배 scaling을 하면 IFFT 변환 결과를 얻을 수 있음. - 개인적으로 이 방법을 가장 선호
Method-IV
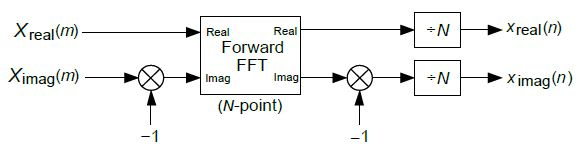
- 입력 샘플을 complex conjugate 후 FFT 변환
- FFT 출력에 다시 complex conjugate 적용
- 자세한 내용은 이전 포스트 참고
- 마지막으로 배 scaling
마치며
IFFT로 FFT를 계산하려면 위 로직을 그대로 사용할 수 있는지 아니면 무엇인가 바꾸어 주어야 하는지 각자 고민해보자^^
