알고리즘의 목적

평면 상에서 고정된 격자 구조가 아닌 임의의 지점에 분포한 유한한 점들의 집합(즉, 포인트 군)의 경계를 찾는 알고리즘이다. 2차 평면상에서 여러 개의 점이 있을 때 그 점 중에서 일부를 이용하여 볼록 다각형을 만들고, 볼록 다각형 내부에 포인트 군의 모든 점을 포함시키킨다. 즉, 볼록 껍질(convex hull)을 찾는 알고리즘으로 연산 복잡도 $O(N\log N)$으로 문제를 풀 수 있는 그라함 스캔 (Graham's Scan) 알고리즘을 사용한다.

참고로 pixel 혹은 격자 구조에 적용할 수 있는 알고리즘으로는 Moore-Neighbor Tracing 알고리즘 등이 있다.

그리고 여기서는 편의상 cross product를 외적으로 번역한다. 실제로 cross product와 outer product를 모두 외적이라 번역하지만 둘의 동작은 다르다.

벡터의 외적으로 CW/CCW 판단하기

Convex Hull 알고리즘의 이해를 돕기 위해 벡터의 외적에 대하여 간단히 리뷰해보자. 3차원 공간에 다음과 같이 두 벡터가 있다고 하자.

두 벡터의 외적은 정의에 의해 다음과 같이 주어진다. 자세한 내용은 위키를 참고하자.

위 식에서 외적의 의미를 보다 명확히 보기 위해 $a_z=b_z=0$이라고 가정하자. 이 가정은 매우 타당하며, 해석의 일반성을 해치지 않는다. 왜냐하면 3차원 공간에서 두 벡터가 span하는 공간은 2차원 평면이고, 이 평면이 $a_z=b_z=0$이 되도록 벡터를 회전해주면 위 가정이 항상 성립하기 때문이다. 좌우지간, $a_z=b_z=0$라고 가정하면, 식 (2)는 다음과 같게 된다.

위 결과로부터 우리는 다음과 같이 중요한 두 가지 사실을 알 수 있다.

• 두 벡터의 외적으로 얻어진 벡터는 두 벡터 $\mathbf{a}$와 $\mathbf{b}$를 포함하는 평면과 항상 직교한다. (법선벡터가 된다.)
• 외적으로 얻어진 벡터의 크기는 외적의 정의에 의해 $\|\mathbf{a}\|\|\mathbf{b}\|\sin(\theta)=a_xb_y-a_yb_x$와 같이 주어진다. 여기서 $\theta$는 두 벡터 간의 사잇각이다. 따라서 다음과 같은 결론을 도출할 수 있다.

  $a_xb_y-a_yb_x$이 양수이면 두 벡터의 사잇각($\theta$)은 양수이다.
  따라서 벡터 $\mathbf{b}$가 벡터 $\mathbf{a}$로부터 반시계 방향(CCW)에 위치한다.

이러한 성질은 이미 잘 알려져있는데 우리는 이것을 아래 그림과 같이 벡터 외적의 오른손 법칙으로 시각화할 수 있다. 아래 그림에서와 같이 벡터 $\mathbf{b}$가 벡터 $\mathbf{a}$로부터 CCW에 위치하면 법선벡터의 부호가 양수이므로 벡터의 방향은 윗쪽을 향하게 된다. 반대의 경우에는 외적의 결과로 얻어진 법선벡터가 아래를 바라보게 된다.

$\|\mathbf{a} \times \mathbf{b} \|$의 기하학적 의미

사실 이 내용은 기초적인 내용이기도 하지만 convex hull을 이해하는데 앞에서 결론을 도출하였기 때문에 별도로 설명할 필요는 없다. 그렇지만 읽는 사람의 편의와 나중을 위해 외적의 결과로 주어진 벡터의 크기가 $\|\mathbf{a} \times \mathbf{b} \|=\|\mathbf{a}\|\|\mathbf{b}\|\sin(\theta)$임을 보이고, 나아가 $\|\mathbf{a}\|\|\mathbf{b}\|\sin(\theta)=a_xb_y-a_yb_x$가 정말 맞는지 확인해보자. 참고로 아래 내용 정리를 위해 아래 링크의 내용을 일부 참고하였다.
참고링크

식 (2)에서 얻은 결과에 의해 $\|\mathbf{a} \times \mathbf{b} \|^2$는 다음과 같다.

따라서 다음이 성립한다.

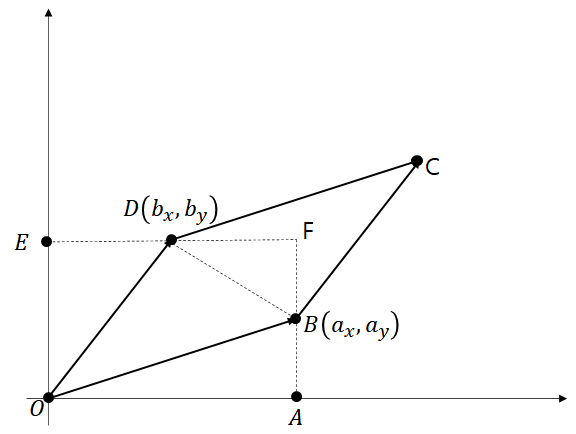
식 (5)는 기하학적으로 위 그림에서 두 벡터 $\mathbf{a}$와 $$\mathbf{b}$의 합벡터로 이루어진 평행사변형의 넓이를 의미한다. 그리고 이 평행사변형의 넓이는 아래 식과 같이 표현할 수도 있다.

따라서 다음이 성립한다.

생각보다 이번 장의 내용이 길어졌다. Convex hull 알고리즘의 이해를 위해서는 두 벡터의 외적으로 얻어진 법선 벡터의 부호에 의해 CW와 CCW가 결정된다는 사실만 기억하면 된다.

Convex Hull 알고리즘

Convex hull 알고리즘을 구현하는 방법은 유일하지 않다. 대표적으로 Jarvis 알고리즘이나 그라함 스캔 방법 등이 있으며, 여기서는 상대적으로 낮은 복잡도로 구현이 가능한 그라함 스캔 방법만을 다룬다.

위와 같은 점들의 집합이 있다고 할 때, Convex hull은 최소의 포인트로 모든 점들이 포함된 경계면을 찾는다. 알고리즘의 동작은 다음과 같다.

알고리즘 수행 절차

2개 이하의 점들로는 다각형을 만들 수 없고 3개의 점으로 만들 수 있는 다각형은 삼각형이 유일하므로 알고리즘의 수행을 위해 최소 4개의 점이 있어야 한다.
1. $y$값이 가장 작은 점을 찾는다. 만약, 둘 이상의 점이 동일한 $y$값을 갖는다면 이들 중 가장 작은 $x$ 값을 갖는 점을 찾는다. 그리고 이 점을 기준점($p_0$)으로 사용한다.
2. $p_0$를 원점으로하여 $p_0$와 나머지 점들 간의 편각을 구한다. 이때, $x$축과 평행한 선을 0도(혹은 최하각도)로 잡는다.
3. 계산된 각도 값을 기준으로 점들을 오름차순 정렬한다.(결과를 Stack 'P'에 저장하였다고 하자. 가장 각도가 작은 점이 stack 상단에 위치한다.)
4. 만약, 둘 이상의 점이 동일한 각도를 갖는다면 기준점과 거리가 가장 멀리 떨어진 점만 남기고 나머지는 'P'에서 제거한다.
5. Stack 'S'를 만들고, $p_0$와 'P'에서 두개의 점 $p_1$과 $p_2$를 꺼내어 'S'에 넣는다.
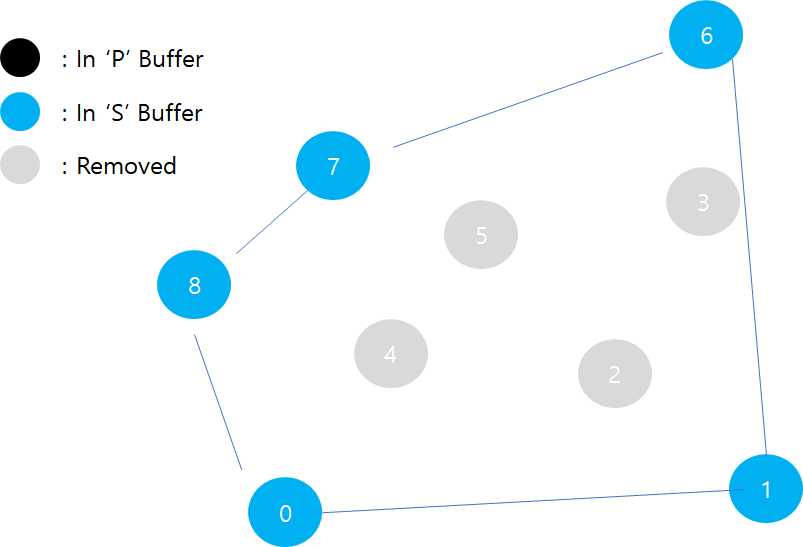
6. 총 $N$개의 점이 있다고 할 때, 'P'에 저장된 나머지 $N-3$개의 점들에 대하여 아래의 절차를 수행한다.

• 'S'의 상단(끝)에서 두 번째로 저장된 포인트를 $x$라 하고, 가장 최근에 저장된 포인트를 $y$라 하자. 그리고 'P' 버퍼의 상단에 저장된 포인트를 $z$라고 하자.
• 두 벡터 차를 $v_1 = y - x$, $v_2 = z - x$와 같이 구하고, $v_1$과 $v_2$의 외적을 계산하여 $v_2$가 $v_1$보다 CCW에 위치해 있는지 확인한다.
• CCW라면 $z$를 'P'에서 꺼내어 'S'에 추가한다.
• CCW가 아니라면 'S'에서 $y$를 꺼내어 버린다. (stack에 마지막으로 저장된 포인트가 $x$가 됨)
• 상기 과정을 반복하고, 'P'에 저장된 모든 점을 방문하면 알고리즘이 종료된다.

7. 'S'에 저장된 값이 convex hull이 된다.

예제

글보다는 그림이 이해하는데 더 도움이 된다. 따라서 알고리즘 수행절차를 예제를 통해 알아보자.

추가: 아래 그림에서 0번 포인트와 6번 포인트를 잇는 벡터가 x축과 이루는 각도가 0번 포인트와 5번 포인트를 잇는 벡터가 x축과 이루는 각도보다 약간 작은데 이것은 그림의 오류이니 감안해서 봐주시기 바랍니다. 알고리즘을 이해하는데 지장은 없습니다.

• 아래와 같은 점들의 집합이 있을 때, y값이 가장 작은 점을 $p_0$로 잡고, $p_0$를 기준으로 각도가 작은 순으로 정렬한다. (번호가 정렬된 순서를 의미)

• $p_0$, $p_1$, $p_2$를 순서대로 'S'에 넣는다. 이하의 모든 예시에서 stack 'S'에 저장된 포인트들은 숫자가 클수록 최근에 저장된 포인트들을 의미한다. 반면, stack 'P'는 숫자가 작을수록 최근에 저장된 포인트들이다.
  

• 아래와 같이 'S'의 상단에서 두 번째로 저장된 1번 포인트를 기준으로 'S' 상단에 저장된 2번 포인트와 'P'의 상단에 저장된 3번 포인트 간의 차벡터(difference vector)를 계산한다. $v_2$가 $v_1$보다 시계 방향에 위치하므로 'S'에서 2번 포인트를 제거한다.
  

• 이제 'S'에는 0번 포인트와 1번 포인트가 저장되어 있다., 따라서 이번에는 0번 포인트를 기준으로 아래와 같이 차벡터를 계산한다. 이번에는 CCW를 만족하므로 3번 포인트를 'S'에 추가한다. (추가한 그림은 다음 step에서 반영하기로 한다.)
  

• 'S'에 포인트가 추가되었으므로 차 벡터를 계산할 때 이제는 1번 포인트를 기준으로 계산한다. CCW를 만족하므로 4번 포인트도 'S'에 추가될 것이다.
  

• 'S'에 포인트가 추가 되었으므로 차벡터를 계산함에 있어 기준이 되는 포인트가 3번 포인트로 변경된다. 아래 그림과 같이 CCW를 만족하지 못하므로 'S'에 최근에 저장한 4번 포인트를 'S'에서 제거한다.
  

• 'S'에서 4번 포인트를 제거하였으므로 이제 'S'에는 0번, 1번 3번 포인트가 순서대로 저장되어 있다. 따라서 아래와 같이 1번 포인트를 기준으로 stack 'S'와 stack 'P' 각각의 상단에 저장된 포인트와의 차벡터를 구한다. CCW를 만족하므로 'P'에 저장된 5번 포인트를 'S'에 추가할 것이다.
  

• 'S'에 5번 포인트를 추가한 후 차벡터를 구해보니 CCW를 만족하지 못하였다. 따라서 'S'에서 5번 포인트를 다시 제거한다.
  

• 바로 이전 단계에서 3번 포인트를 기준으로 경로를 계산하였는데 유효하지 않아 'S'에서 5번 포인트를 제거하였따. 이는 3번 포인트를 기준으로 찾은 경로가 유효않음을 의미한다. 따라서 기준 점을 1번 포인트로 변경 후 차벡터를 구해보면 CCW를 또 만족하지 못한다. 그래서 3번 포인트도 'S'에서 제거할 것이다.
  

• 앞에서 반복적으로 계산 과정을 살펴보았으니 남은 과정들은 그림으로 대체한다.
  
  
  

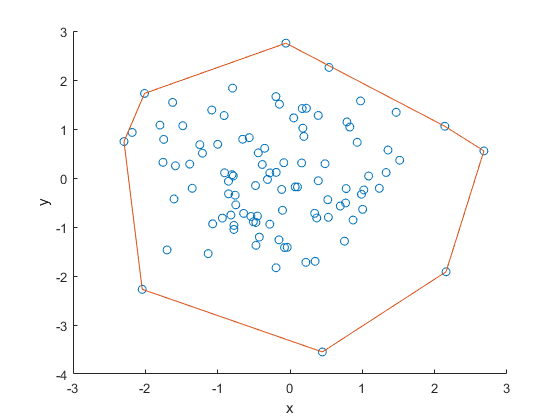
• 'P'의 모든 포인트들을 방문하였으므로 알고리즘은 종료된다. 'S'에 저장된 점들을 연결하면 아래와 같이 모든 점들이 포함된 다각형이 그려진다.
  

예제 코드

아래 코드는 테스트를 위해 MATLAB으로 대충 짜본 것이다. 솔직히 각도가 동일할 때, 거리가 먼 포인트만 남겨주는 부분이 제대로 도는지는 모르겠다ㅡㅡ; 랜덤하게 포인트를 생성하였더니 이런 경우가 잘 발생하지도 않고 알고리즘의 핵심이 이 부분은 아니라서 일단 핵심 동작을 확인하는 것에 초점을 맞추었다. 어쨌든 아래와 같이 동작은 잘 하는 것 같다.

clear;
clc;


X_IDX = 1;
Y_IDX = 2;

nPts = 100; % at least 4 points required
p = randn(nPts, 2);

%% find bottom-most point. If there are multiple points with the same y value, then, a point with smaller x value is selected.
[~, minYIdx] = min(p(:, Y_IDX));
if length(minYIdx) > 1
    [~, minXIdx] = min(p(minYIdx, X_IDX));
    p0 = p(minYIdx(minXIdx), :);
    
else
    p0 = p(minYIdx,:);
end
p = [p(1:minYIdx-1,:); p(minYIdx+1:end,:)];

%% sort the reminaing N-1 points w.r.t. polar angle in CCW around p0 in ascending order
pt = p - p0; 
angleVal = atand(-pt(:,X_IDX)./pt(:,Y_IDX));
[sortedAngle, sortIdx] = sort(angleVal, 'ascend'); % -90deg <= angle < 90deg
pt = pt(sortIdx,:);

%% If more than two points have the same angle, then remove all points except the point farthest from p0
angleDiff = sortedAngle(2:end) - sortedAngle(1:end-1);
sameAngleIdx = find(angleDiff == 0);
if ~isempty(sameAngleIdx)
    removeFlag = zeros(length(sameAngleIdx)+1);
    preCheckIdx = 0;
    preMaxRange = 0;
    for i = 1:length(sameAngleIdx)
        ptsIdx = sameAngleIdx(i);
        idx1 = ptsIdx; 
        idx2 = ptsIdx + 1; 
        
        preCheckIdx = idx2;
        
        if (idx1 == preCheckIdx)
            curRange = p(idx2,X_IDX)^2 + p(idx2,Y_IDX)^2; % square-root omitted
            if (curRange > preMaxRange)
                removeFlag(i) = 1;                
                preMaxRange = curRange;
            else
                removeFlag(i+1) = 1;                
            end
        else
            range1 = p(idx1,X_IDX)^2 + p(idx1,Y_IDX)^2; 
            range2 = p(idx2,X_IDX)^2 + p(idx2,Y_IDX)^2; 
            if (range1 < range2)
                removeFlag(i) = 1;                
                preMaxRange = range2;
            else
                removeFlag(i+1) = 1;                
                preMaxRange = range1;
            end
        end
    end
end

%% Create an empty stack ‘S’ and push points[0], points[1] and points[2] to S.
stackBuf = zeros(nPts, 2);
stackBuf(1:3,:) = [[0, 0];
                   pt(1:2,:)];

%% Process remaining N-3 points one by one
ptsIdx = 3;
stackIdx = 2;
while true
    x0 = stackBuf(stackIdx, :);    
    y0 = stackBuf(stackIdx+1,:);
    
    if (ptsIdx > nPts-1)
        y1 = [0, 0];
    else
        y1 = pt(ptsIdx,:);        
    end  

    
    v1 = y0 - x0;
    v2 = y1 - x0;
    
    ccw = v1(X_IDX)*v2(Y_IDX) - v1(Y_IDX)*v2(X_IDX);
    if ccw > 0
        if (ptsIdx > nPts-1)
            break;
        end
        ptsIdx = ptsIdx + 1;
        stackIdx = stackIdx + 1;
        stackBuf(stackIdx + 1,:) = y1;
    else
        stackIdx = stackIdx - 1;
    end    
end

%% 
convelhull = [[0,0];stackBuf(1:stackIdx+1,:);[0,0]] + p0;

p = [p0; p];

figure;
scatter(p(:, X_IDX), p(:, Y_IDX))
hold on
plot(convelhull(:, X_IDX), convelhull(:, Y_IDX))
hold off
xlabel('x')
ylabel('y')

아래 링크에 가면 C++ 예제코드도 확인해볼 수 있다.
https://www.geeksforgeeks.org/convex-hull-set-2-graham-scan/