Number Structure

Clear·2023년 5월 2일

초록색과 같은 색상의 Keyword 는 한번 쯤 읽어볼만한 소재입니다.

노란색과 같은 색상의 Keyword 는 꼭 알아두어야 할 소재입니다.

파란색과 같은 색상의 Keyword 는 부가설명입니다.

마지막으로 Game Math 글의 모든 Image 출저는 '이득우의 게임 수학' 임을 밝힙니다.

Set Theory

추상적 대상들의 모임인 Set 을 연구하는 수학이론

Set | 집합
Theory | 이론

Native Set Theory

서로 구분되는 Element로 구성된 묶음을 바라보는 Set Theory

Element | 원소

Native Set Theory

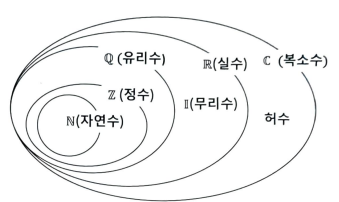
Venn Diagram

Proposition

참과 거짓으로 명확하게 구분할 수 있는 것

Proposition | 명제

Axiom

Proposition 중 증명할 필요가 없는 Basic Proposition

Axiom | 공리

Axiom Set Theory

Axiom 을 기반으로 대상을 구분하는 Set Theory 로 수가 가지는 Opeartion에
대한 Axiom 을 기반으로 수를 분류한다.

Operation | 연산

Binary Opearation

Number Set 의 고유한 특징으로 Element 를 이용하여 Opeartion 을 하며
두 개의 Element 를 사용하여 새로운 Element 를 만들어 낸다.

Binary Operation | 이항연산

Closure

같은 Set에 속한 두 수를 투입한 Binary Operation의 결과가 항상 투입한 Set에 속한다면
그 Binary Operation 을 Closure 라고 한다.

Closure | 닫혀있다

Commutaitve law

임의의 두 수 a 와 b를 Operation 할 때 순서와 관계 없이 항상 동일한 결과가 나오는 성질

a + b = b + a
a * b = b * a

Commutaitve law | 교환 법칙

Associative law

Operation 이 두 번 이상 연속될 때, 앞의 Opearation을 먼저 계산한 결과와
뒤의 Operation 을 계산한 결과가 같은 성질

( a + b ) + c = a + ( b + c )
( a * b ) * c = a * ( b * c )

Associative law | 결합 법칙

Distributive law

두 Binary Operation 에 대해

Left Distributive
a * ( b + c ) = a * b + a * c

right Distributive
( b + c ) * a = b * a + c * a

가 나오는 성질

Distributive law | 분배 법칙

Indentity

임의 수와의 Operation 결과를 항상 동일한 수로 만들어주는 특별한 수
실수 집합의 덧셈의 Indentity 는 0 이며 곱셈은 1 이다.

Indentity | 항등원

Inverse

Operation 의 결과를 항상 Identity 로 만들어주는 수
덧셈의 Inverse 는 Opposite number, 곱셈의 Inverse 는 Reciprocal 이라 한다.

Inverse | 역원
Opposite numver | 반대수
Reciprocal | 역수

Field

Operation 에 대해 Closure.

Operation 에 대해 Associative law 가 성립한다.

Operation 에 대한 Identity 가 존재한다.

Operation 에 대한 Inverse 가 존재한다.

Operation 에 대해 Commutative law 가 성립한다.

위 5 가지 Axiom 을 만족하는 Opearation 은 정수의 덧셈, 실수의 덧셈, 곱셈등이 존재한다.
만족하지 않은 Operation 같은 경우 정수의 뺼셈등이 존재한다. ( Commutaive law 등이 성립 불가 )

두 번째 Operation 에 대해 Closure

두 번째 Operation 에 대해 Associative law 가 성립한다.

첫 번째 Operation 과 두 번째 Operation 에 대해 Distributive law 가 성립한다.

두 번째 Operation 에 대해 Commutative law 가 성립한다.

두 번째 Operation 에 대한 Identity 가 존재한다.

두 번째 Operation 에 대한 Inverse 가 존재한다.

이 11 가지에 대한 Axiom 을 모두 만족하는 Operation 은 실수의 덧셈과 곱셈등이 존재한다.

이렇게 Axiomatic Set Theory 에서 두 Operation 에 대하여 1번 부터 11번까지의
Axiom을 모두 만족하는 Number Set을 Field 의 구조를 지난다고 표현한다.

Field | 체
Number Set | 수집합

수의 시각화

Number line

위와 같이 유리수의 Element를 순서대로 나열시키고 빈틈에 무리를 채워
연속성을 가지는 직선으로 시각화 한 것을 Number line 이라한다.

Number line 에서는 특정 Element 에 고유한 위치를 갖게 하여 다음과 같이
점을 통하여 수를 표현할 수 있다.

Absolute value

수가 가지는 방향의 속성을 부호를 사용하여 나타내며 크기의 속성은 원점으로의 거리를 의미한다.
어떤 수의 원점으로 거니는 Vertical Bar 를 통하여 나타내며 이를 Absolute value 라 한다.