2025.4.6 알고리즘 코드카타

알고리즘 코드카타 - 113. 전력망을 둘로 나누기

문제 링크

인접 리스트 참고 : https://velog.io/@eunchae2000/자료구조-그래프를-저장하는-방법-3가지-인접-행렬-인접-리스트-간선-리스트-with-Python

문제 설명

n개의 송전탑이 전선을 통해 하나의 트리 형태로 연결되어 있습니다. 당신은 이 전선들 중 하나를 끊어서 현재의 전력망 네트워크를 2개로 분할하려고 합니다. 이때, 두 전력망이 갖게 되는 송전탑의 개수를 최대한 비슷하게 맞추고자 합니다.

송전탑의 개수 n, 그리고 전선 정보 wires가 매개변수로 주어집니다. 전선들 중 하나를 끊어서 송전탑 개수가 가능한 비슷하도록 두 전력망으로 나누었을 때, 두 전력망이 가지고 있는 송전탑 개수의 차이(절대값)를 return 하도록 solution 함수를 완성해주세요.

---

제한사항

• n은 2 이상 100 이하인 자연수입니다.
• wires는 길이가 n-1인 정수형 2차원 배열입니다.
• wires의 각 원소는 [v1, v2] 2개의 자연수로 이루어져 있으며, 이는 전력망의 v1번 송전탑과 v2번 송전탑이 전선으로 연결되어 있다는 것을 의미합니다.
• 1 ≤ v1 < v2 ≤ n 입니다.
• 전력망 네트워크가 하나의 트리 형태가 아닌 경우는 입력으로 주어지지 않습니다.

---

입출력 예

n	wires	result
9	[[1,3],[2,3],[3,4],[4,5],[4,6],[4,7],[7,8],[7,9]]	3
4	[[1,2],[2,3],[3,4]]	0
7	[[1,2],[2,7],[3,7],[3,4],[4,5],[6,7]]	1

입출력 예 설명
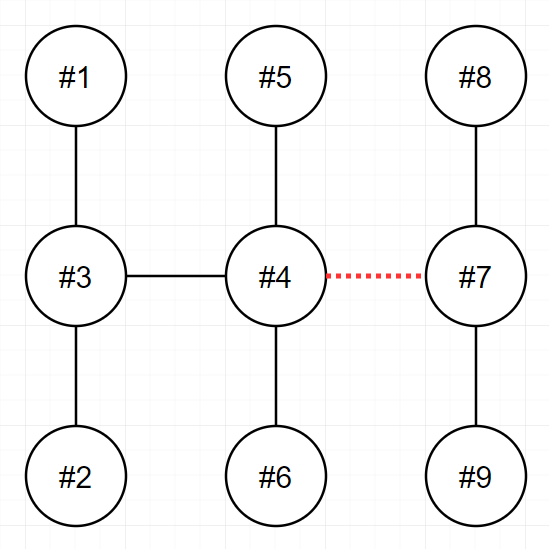
입출력 예 #1

• 다음 그림은 주어진 입력을 해결하는 방법 중 하나를 나타낸 것입니다.
  
• 4번과 7번을 연결하는 전선을 끊으면 두 전력망은 각 6개와 3개의 송전탑을 가지며, 이보다 더 비슷한 개수로 전력망을 나눌 수 없습니다.
  또 다른 방법으로는 3번과 4번을 연결하는 전선을 끊어도 최선의 정답을 도출할 수 있습니다.

입출력 예 #2

• 다음 그림은 주어진 입력을 해결하는 방법을 나타낸 것입니다.
  
  -2번과 3번을 연결하는 전선을 끊으면 두 전력망이 모두 2개의 송전탑을 가지게 되며, 이 방법이 최선입니다.

입출력 예 #3

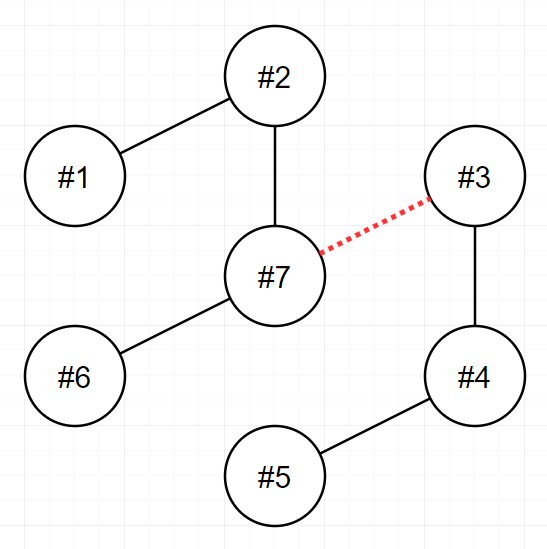
• 다음 그림은 주어진 입력을 해결하는 방법을 나타낸 것입니다.
  
• 3번과 7번을 연결하는 전선을 끊으면 두 전력망이 각각 4개와 3개의 송전탑을 가지게 되며, 이 방법이 최선입니다.

풀이 코드

#include <string>
#include <vector>
#include <algorithm>
#include <cmath>

using namespace std;

// 정점(발전소)을 연결하는 간선추가
void addEdge(vector<vector<int>>& graph, int a, int b)
{
    graph[a].push_back(b);
    graph[b].push_back(a);
}
// 간선 연결 끊기
void removeEdge(vector<vector<int>>& graph, int a, int b)
{
    graph[a].erase(remove(graph[a].begin(), graph[a].end(), b), graph[a].end());
    graph[b].erase(remove(graph[b].begin(), graph[b].end(), a), graph[b].end());
}

// 연결된 노드들이 몇 개인지 반환
int DFS(int node, vector<vector<int>>& graph, vector<bool>& visited)
{
    visited[node] = true;
    int nodecount = 1;
    
    for(int neighbor : graph[node])
    {
        if(!visited[neighbor])
        {
            nodecount += DFS(neighbor, graph, visited);
        }
    }
    return nodecount;
}

int solution(int n, vector<vector<int>> wires) {
    int answer = 100;
    int nodecount = 1;
    vector<vector<int>> graph(n+1);
    
    // 인접 리스트 생성
    for(auto& wire : wires)
    {
        addEdge(graph, wire[0], wire[1]);
    }
    // 각 연결을 순회하면서 해당 연결을 끊고나서 남은 연결된 발전소 개수 확인
    for(auto& wire : wires)
    {
        int a = wire[0], b = wire[1];
      	
        removeEdge(graph, a, b);
        
        vector<bool> visited(n+1, false);
        int componentSize = DFS(a, graph, visited);
        // 백트래킹
        addEdge(graph,a,b);
        
        answer = min(answer,abs(n - 2 * componentSize));
    }
    
    return answer;
}

• 인접 리스트(간선 리스트)와 DFS를 이용한 풀이. 코드 구성은 아래와 같다.

  1. 그래프 모델링 및 백트래킹을 위한 addEdge() 함수
  2. 간선을 끊는 removeEdge() 함수
  3. 문제에서 요구하는 연결된 노드의 수를 구하기 위한 DFS()

• 노드를 중복 계산하면 안되기 때문에 그래프와 동일한 크기의 방문 배열 visited를 선언.

• 주어지는 전선 정보(간선 정보)를 순회하며 연결을 끊어본다. 연결을 끊고 한쪽 노드를 선택해 연결된 노드들을 모두 탐색한다.

• DFS()는 호출될 때마다 nodecount 값이 증가하는 구조. 따라서 최종적으로 main 함수에선 최초 호출 노드와 연결된 노드의 수를 반환하게 된다.

• 두 그룹의 노드 수 차이는 아래와 같다.

  abs(n - 2 * componentSize)

  예를 들어, 전체 노드가 10개이고 한 그룹의 크기가 4라면
  다른 그룹의 크기는 6이고 차이는 2(즉, |10 - 2×4| = 2)이기 때문이다.