
Word Embedding이란?
- 워드 임베딩(Word Embedding)은 자연어 처리에서 단어를 벡터로 표현하는 방법으로, 단어를 Dense Representation으로 변환한다.
Sparse Representation(희소표현)
먼저 원-핫 벡터는 표현하고자 하는 단어의 index값만 1이고 나머지는 전부 0으로 채워넣은 벡터표현 방법이다. 이렇게 벡터 또는 행렬의 값이 대부분 0으로 표현되는 방법을 Sparse Representation이라고 한다. 그래서 원-핫 벡터는 sparse vector이다.
희소 벡터의 문제점은 단어의 개수가 늘어나면 벡터의 차원이 한없이 커진다는 점이다. 예를들어 강아지 = [ 0 0 0 0 1 0 0 0 0 0 0 0 ... 중략 ... 0]이라는 원-핫벡터를 보면 index=4의 값인 1 뒤에 0은 낭비를 일으킨다. 이러한 벡터 표현은 공간적 낭비를 불러일으키기 때문에, 원-핫 벡터와 같은 희소 벡터의 문제점은 단어의 의미를 표현하지 못한다는 점이다.
Dense Representation(밀집표현)
Sparse Representation과 반대되는 표현으로 Dense Representation이 있다. 밀집 표현은 벡터의 차원을 단어 집합의 크기로 상정하지 않고 사용자가 설정한 값으로 모든 단어의 벡터 표현의 차원을 맞춘다. 또한, 이 과정에서 더 이상 0과 1만 가진 값이 아니라 실수값을 가지게 된다.
Ex) 강아지 = [ 0 0 0 0 1 0 0 0 0 0 0 0 ... 중략 ... 0] # 이때 1 뒤의 0의 수는 9995개. 차원은 10,000
예를 들어 10,000개의 단어가 있을 때 강아지란 단어를 표현하기 위해서는 위와 같은 표현을 사용했다. 하지만 밀집 표현을 사용하고, 사용자가 밀집 표현의 차원을 128로 설정한다면, 모든 단어의 벡터 표현의 차원은 128로 바뀌면서 모든 값이 실수가 된다.
Ex) 강아지 = [0.2 1.8 1.1 -2.1 1.1 2.8 ... 중략 ...] # 이 벡터의 차원은 128
이 경우 벡터의 차원이 조밀해졌다고 하여 밀집 벡터(dense vector)라고 한다.
Word Embedding(워드 임베딩)
단어를 밀집 벡터(dense vector)의 형태로 표현하는 방법을 워드 임베딩(word embedding)이라고 한다. 그리고 이 밀집 벡터를 워드 임베딩 과정을 통해 나온 결과라고 하여 임베딩 벡터(embedding vector)라고도 한다.
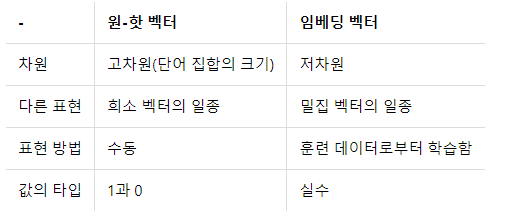
워드 임베딩 방법론으로는 LSA, Word2Vec, FastText, Glove 등이 있으며, 단어를 랜덤한 값을 가지는 밀집 벡터로 변환한 뒤에, 인공 신경망의 가중치를 학습하는 것과 같은 방식으로 단어 벡터를 학습하는 방법을 사용한다. 아래의 표는 앞서 배운 원-핫 벡터와 지금 배우고 있는 임베딩 벡터의 차이를 보여준다.
참고자료
https://wikidocs.net/33520 <딥 러닝을 이용한 자연어 처리 입문>
