[4주차 목표]
1. 👉선형 회귀에 대한 기초👈
2. scikit-learn을 이용한 선형 회귀
3. 자전거 수요 예측해보기

○ 선형 회귀 기초

• 어떤 수치에 의해 다른 수치가 영향을 받고 있다고 한다면, 다른 변수의 값을 변하게 하는 변수를 독립 변수 (x, independent variable), 이에 의해 값이 종속적으로 변하는 변수를 종속 변수 (y, dependent variable, observation)라고 한다.

• 선형회귀는 한 개 이상의 독립변수 x와 y의 선형 관계를 모델링한다.
  

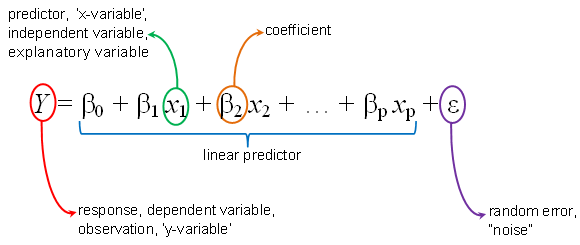
• 독립 변수 x가 1개라면 식은 아래와 같다.

y = wx + b

여기서 독립 변수 x와 곱해지는 값 w를 머신러닝에서는 가중치 (weight), 별도로 더해지는 값 b를 편향 (bias) 또는 상수 (constant)라고 한다.

• 선형회귀는 주어진 데이터로부터 y와 x의 관계를 가장 잘 나타내는 직선을 그리는 일을 말한다. 이를 결정하는 것이 w와 b의 값이므로 적절한 w와 b를 찾아내는 것이 일이다.

• 다중 선형 회귀 (Multiple Linear Regression) : x가 여러 개일 때, 즉 종속 변수에 영향을 주는 요소가 여러개 일 때를 말한다.

○ 회귀 (regression)와 분류 (classification)

○ scikit-learn 패키지를 이용한 선형 회귀분석

👉 지난 학기의 점수 데이터 (중간, 기말, 과제) 와 최종 성적 데이터를 이용하여 현재 학기 최종 성적 예측하기

1) 지난 학기 데이터 가져오기
2) 모델을 이용해 학습시키기
3) 가중치, 편향 알아보기
4) 이번 학기 성적 예측하기

1) 지난 학기 데이터 가져오기

import numpy as np
X = np.array([[70,85,11],[71,89,18],[50,80,20],[99,20,10],[50,10,10]]) # 중간, 기말, 가산점
y = np.array([73,82,72,57,34]) # 최종 성적

2) 모델을 이용하여 학습시키기

sklearn 패키지의 LinearRegression 클래스를 사용한다.

from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(X, y)

lr = LinearRegression() 객체를 생성한 뒤에 fit()을 통해 지난 학기 데이터를 학습시킨다. 학습을 하며 모델은 적정한 가중치와 편향을 찾아낸다. 샘플 하나 당 3개의 독립변수가 있으므로 3개의 가중치를 찾을 것이다.

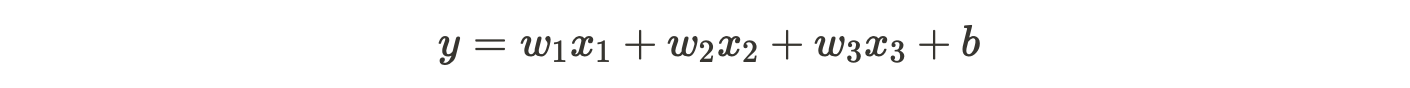
3) 가중치, 편향 알아보기

• lr.coef_ : 가중치 출력

lr.coef_
#result
array([0.38823654, 0.40424492, 0.98136214])

3차원 벡터가 출력되며, 각각 변수에 대한 가중치이다.
위의 식에서 가중치에 해당하는 w1, w2, w3의 값이다.

• lr.intercept_ : 편향 출력

lr.intercept_
#result
0.6960065780730318

위의 식에서 b에 해당하는 값이다.

4) 이번 학기 성적 예측하기

이제 식을 알았으니 이번 학기 성적을 predict()를 이용하여 최종 성적을 예측할 수 있다.

new_data = [[60, 70, 80], [71, 90, 15]]
y_new = lr.predict(new_data)
y_new

#result
array([130.79631462,  79.36327551])

각각 130점, 79점대가 예상된다.

가중치, 편향을 직접 대입하여 맞는 지도 확인해본다.

#실제 계산
lr.coef_[0]*60+lr.coef_[1]*70+lr.coef_[2]*80+lr.intercept_

#result
130.79631462275842