---

개요

머신러닝 모델에 따른 평가지표 이해 및 숙달하기

---

📌 평가지표

1. 모델 성능 평가

• 모델 성능평가란, 실제값과 모델에 의해 예측된 값을 비교해 두 값의 차이 (오차)를 구하는 것이다.
• 실제값 - 예측값 = 0 이 되면 오차가 없는 것으로, 모델 성능은 당연하게도 오차가 적을수록 좋다.
  • 모델 성능 평가는 결과 변수(답)이 있어야 성능이 좋은지 아닌지 확인할 수 있기 때문에,
    지도학습에서만 사용할 수 있다.
  • 모델링의 목적이나 목표 변수의 유형애 따라 다른 평가지표들을 사용한다.

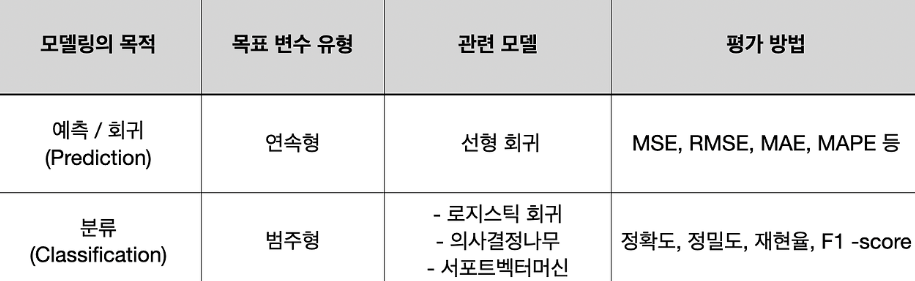
2. 평가 지표의 종류
   • 모델링의 목적에 따라 크게 분류와 회귀로 나뉘어지며,
     각 모델에 따라 평가 방법이 다르다.

     • 분류 : *F1 - score , *ROC-AUC , 정확도 , 정밀도 , 재현율 등
       • 다중분류 평가지표
       • 이중분류 평가지표
     • 회귀 : *R-squared, *RMSE , MSE, MAE 등
       • 회귀 평가지표

---

📌 목적 1

• 머신러닝 모델은 Train 데이터로 학습 후 Test 데이터로 결과를 확인하는데,
  Train 데이터로 학습 후 Test 데이터를 입력해 예측한 결과를 바로 제출하게 되면
  해당 모델의 학습이 제대로 되었는지, 더 최적화할수는 없는지 등을 확인할 수 없게 된다.
• 따라서, Train 데이터를 학습용과 검증용으로 분리하여 모델의 성능을 확인하고,
  최적화한 후에, Test 데이터를 입력한 결과를 제출하는 것이 좋다.

검증용 데이터를 입력한 결과가 최적화가 되어있는지,
모델의 성능이 좋은지 확인하기 위해
평가지표를 확인해야 한다!

---

📌 목적 2

• Train 과 Test 데이터 2가지만 제시되는 경우
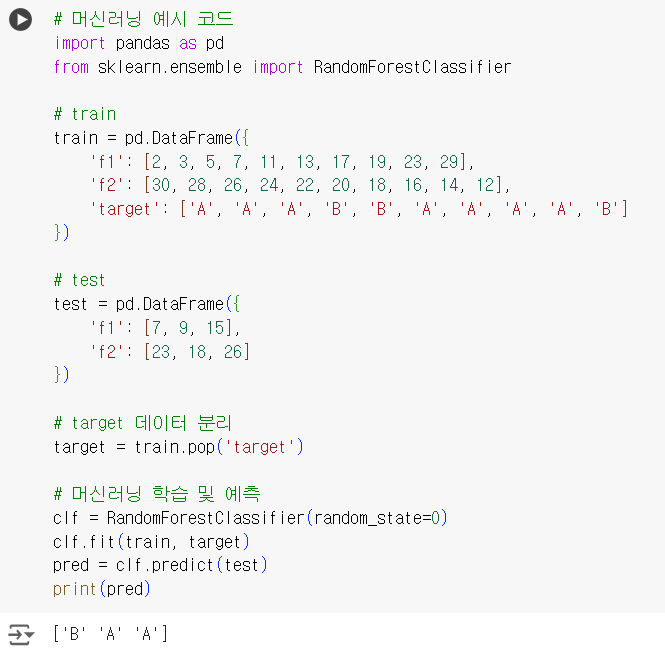
  아래 코드처럼 train 데이터로 모델 학습 후 test 데이터로 예측을 실행하고
  해당 예측 결과를 pred라는 변수에 담아 제출하면 끝이 난다.

# 머신러닝 예시 코드
import pandas as pd
from sklearn.ensemble import RandomForestClassifier
# train
train = pd.DataFrame({
    'f1': [2, 3, 5, 7, 11, 13, 17, 19, 23, 29],
    'f2': [30, 28, 26, 24, 22, 20, 18, 16, 14, 12],
    'target': ['A', 'A', 'A', 'B', 'B', 'A', 'A', 'A', 'A', 'B']
})
# test
test = pd.DataFrame({
    'f1': [7, 9, 15],
    'f2': [23, 18, 26]
})
# target 데이터 분리
target = train.pop('target')
# 머신러닝 학습 및 예측
clf = RandomForestClassifier(random_state=0)
clf.fit(train, target)
pred = clf.predict(test)
print(pred)

• 하지만 이렇게 예측을 하게 되면 해당 모델링이 제대로 되었는지,
  예측값이 잘 나오는지 확인할 수 있는 방법이 없게 된다.

---

• 그렇기 때문에 train 데이터를 2~30% 비율로 분리를 하여 validation (검증용) 데이터를 확보해주고,
  모델 학습 후 val 데이터를 입력해 나온 예측값에 대한 결과물을 평가지표들을 통해 성능을 평가하는 것이다.

# 머신러닝 예시 코드(predict)
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score
train = pd.DataFrame({
    'f1': [2, 3, 5, 7, 11, 13, 17, 19, 23, 29],
    'f2': [30, 28, 26, 24, 22, 20, 18, 16, 14, 12],
    'target': ['A', 'A', 'A', 'B', 'B', 'A', 'A', 'A', 'A', 'B']
})
# 검증 데이터 분리
target = train.pop('target')
X_train, X_val, y_train, y_val = train_test_split(train, target, test_size=0.3, random_state=0)
# 머신러닝 학습 및 예측
clf = RandomForestClassifier(random_state=0)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_val)
print("val:", y_pred) # 예측값
print("정확도:", accuracy_score(y_val, y_pred)) # 정확도 평가
# test
test = pd.DataFrame({
    'f1': [7, 9, 15],
    'f2': [23, 18, 26]
})
pred = clf.predict(test)
print("test:", pred)

---

📌 분류

---

📌 이중분류 평가지표

# 이진분류 데이터
# 크게 0과 1로 분류되는 실제, 예측값 / 'A', 'B' 등 문자열로 분류되는 실제, 예측값이 있다.
import pandas as pd
y_true = pd.DataFrame([0, 1, 1, 0, 0, 1, 1, 1, 1, 0]) #실제값
y_pred = pd.DataFrame([0, 0, 1, 1, 0, 0, 0, 1, 1, 0]) #예측값
y_true_str = pd.DataFrame(['B', 'A', 'A', 'B', 'B', 'A', 'A', 'A', 'A', 'B']) #실제값
y_pred_str = pd.DataFrame(['B', 'B', 'A', 'A', 'B', 'B', 'B', 'A', 'A', 'B']) #예측값

---

ROC-AUC ( * 중요 ! )

• ROC 분석? (Receiver Operating Characteristic Curve)

  민감도와 1 - 특이도 로 그려지는 곡선.

• 오차행렬표에 대한 이해

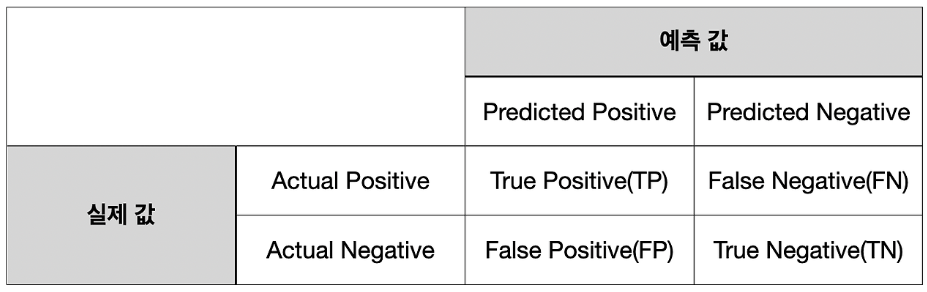
  오차 행렬은 분류의 예측 범주와 실제 데이터의 분류 범주를 교차 표 형태로 정리한 행렬
  

• 민감도와 특이도

  ROC Curve에 활용되는 값은 민감도(Sensitivity)와 특이도(Specificity) !

  • 민감도(SE) = TP / TP + FN : 실제 양성 (Actual Positive) 대 맞춘 양성 (True Positive) 의 비율
    • 양성으로 예측해서 맞췄거나 음성으로 예측했는데 틀린 경우를 합친 것이 실제 양성에 해당
      (위 표를 참고!)
      음성으로 예측했는데 틀린 경우 (FN)의 비중이 낮을수록 검사의 정확성이 증가하기 때문에
      민감도는 클수록 좋다!

  • 특이도(SP) = TN / TN + FP : 실제 음성 (Actual Negative) 대 맞춘 음성 (True Negative) 의 비율
    • 음성으로 예측해서 맞췄거나 양성으로 예측했는데 틀린 경우를 합친 것이 실제 음성에 해당
      (위 표를 참고!)
      특이도도 민감도와 마찬가지로 클수록 좋다.
      실제 양성인 값을 제대로 판단하는 비율이 크더라도 음성인 값을 제대로 걸러내지 못한다면
      검사 전체의 정확성이 떨어질 수 있기 때문이다.
      특이도의 값이 클수록 실제 음성인 값을 잘 필터링한다는 것이기에 (FP)의 비중이 낮을수록 좋다.

• ROC CURVE
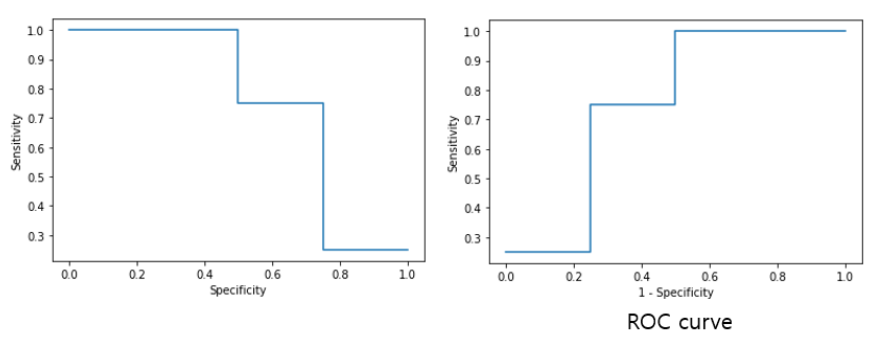
  X축은 (1 - 특이도), Y축은 민감도가 되는 곡선 그래프

  • ROC는 민감도(SE)와 특이도(SP)의 관계를 그래프로 나타낸 것인데,
    실제로는 민감도(SE)와 FPR(=1-SP)을 그래프로 나타낸다.
    그래야 우리에게 익숙하고 읽기 쉬운 우상향 그래프로 표현되기 때문
    

• AUC(Area Under the Curve)
  AUC는 ROC curve의 곡선 아래 영역을 나타내며 1에 가까울수록 성능이 우수하다고 판단한다.
  0.5인 경우 최악의 성능. (모델이 분류 능력이 없다고 보면 된다.)
  만약, AUC 값이 0.5 미만이라면 Labeling 또는 Algorithm 이 잘못되었을 가능성이 크다.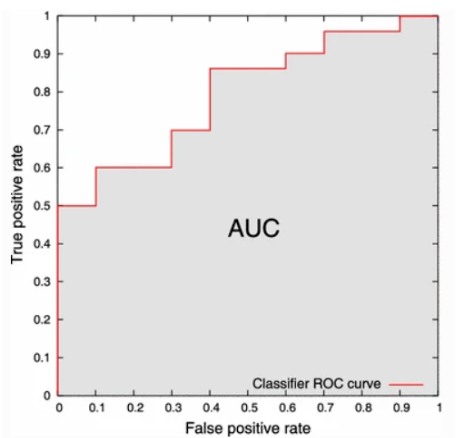

  

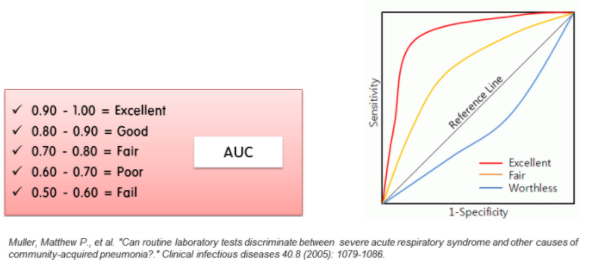
• AUC 면적에 대한 평가기준 (2005년)

  

---

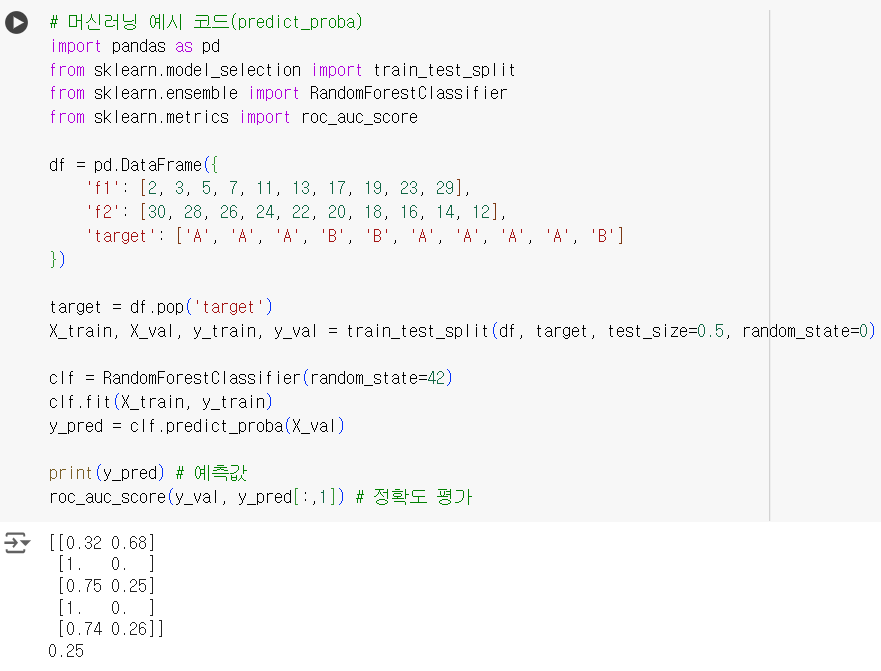
# 머신러닝 예시 코드(predict_proba)
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import roc_auc_score
df = pd.DataFrame({
    'f1': [2, 3, 5, 7, 11, 13, 17, 19, 23, 29],
    'f2': [30, 28, 26, 24, 22, 20, 18, 16, 14, 12],
    'target': ['A', 'A', 'A', 'B', 'B', 'A', 'A', 'A', 'A', 'B']
})
target = df.pop('target')
X_train, X_val, y_train, y_val = train_test_split(df, target, test_size=0.5, random_state=0)
clf = RandomForestClassifier(random_state=42)
clf.fit(X_train, y_train)
y_pred = clf.predict_proba(X_val)
print(y_pred) # 예측값
roc_auc_score(y_val, y_pred[:,1]) # 정확도 평가

# ROC-AUC ***
from sklearn.metrics import roc_auc_score
import numpy as np
# 실제값 (0: 음성, 1: 양성)
y_true = pd.DataFrame([0, 1, 0, 1, 1, 0, 0, 0, 1, 1])
# 예측값 중 양성(1) 확률
y_pred_proba = np.array([
    [0.8, 0.2],
    [0.1, 0.9],
    [0.77, 0.23],
    [0.6, 0.4],
    [0.2, 0.8],
    [0.4, 0.6],
    [0.6, 0.4],
    [0.8, 0.2],
    [0.3, 0.7],
    [0.4, 0.6]
])
roc_auc = roc_auc_score(y_true, y_pred_proba[:,1])
print("ROC-AUC:", roc_auc)

y_true_str = pd.DataFrame(['B', 'A', 'A', 'B', 'B', 'A', 'A', 'A', 'A', 'B']) #실제값
y_pred_proba_str = np.array([
    [0.8, 0.2],
    [0.1, 0.9],
    [0.77, 0.23],
    [0.6, 0.4],
    [0.2, 0.8],
    [0.4, 0.6],
    [0.6, 0.4],
    [0.8, 0.2],
    [0.3, 0.7],
    [0.4, 0.6]
]) # 예측값
roc_auc = roc_auc_score(y_true, y_pred_proba_str[:,1])
print("ROC-AUC:", roc_auc)

---

F1 스코어 ( * 중요 ! )

정밀도와 재현율을 결합해 만든 지표,
정밀도와 재현율이 어느 한 쪽으로 치우치치 않는 수치를 나타낼 때 F1 스코어는 높은 값을 가진다.
F1 Score = 2 * Precision(정밀도) * Recall(재현율) / (Precision + Recall)

• F1 스코어는 0 ~ 1 사이의 값을 가지며, 1에 가까울수록 성능이 좋다는 것을 의미한다.

# F1 스코어(F1 Score) ***
from sklearn.metrics import f1_score
f1 = f1_score(y_true, y_pred)
print("F1 스코어:", f1)

# 문자열 분류 데이터는 정답이 되는 값(양성값)을 설정해줘야 한다.
f1 = f1_score(y_true_str, y_pred_str, pos_label='A') # positive label : 양성값 설정
print("F1 스코어:", f1)

---

정확도

전체 데이터 중 정확하게 예측한 데이터의 수,
정확도는 불균형한 데이터의 경우에는 적합하지 않은 평가지표이다.
정확도 = TP + TN / TP + TN + FP + FN

# 정확도(Accuracy)
from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y_true, y_pred)
print("정확도:", accuracy)

accuracy = accuracy_score(y_true_str, y_pred_str)
print("정확도:", accuracy)

---

📌 다중분류 평가지표

• 예측해야 하는 값이 2가지가 아닌 3가지 이상인 분류

# 다중분류 데이터
y_true = pd.DataFrame([2, 2, 3, 3, 2, 1, 3, 3, 2, 1]) # 실제값
y_pred = pd.DataFrame([2, 2, 1, 3, 2, 1, 1, 2, 2, 1]) # 예측값
y_true_str = pd.DataFrame(['B', 'B', 'C', 'C', 'B', 'A', 'C', 'C', 'B', 'A']) # 실제값
y_pred_str = pd.DataFrame(['B', 'B', 'A', 'C', 'B', 'A', 'A', 'B', 'B', 'A']) # 예측값

---

📌 F1 스코어 ( * 중요 ! )

• 다중분류에서는 average = 인자에 신경을 써야 한다.

  micro 평균은 모든 클래스의 거짓 양성(FP), 거짓 음성(FN), 진짜 양성(TP)의 총 수를 헤아린 다음,
  정밀도, 재현율, f1-점수를 이 수치로 계산한다.

  macro 평균은 클래스별 f1-점수에 가중치를 주지 않는다.
  클래스 크기에 상관없이 모든 클래스를 같은 비중으로 다룬다.

  weighted 평균은 클래스별 샘플 수로 가중치를 두어 f1-점수의 평균을 계산한다.

• 각 샘플을 똑같이 간주한다며 micro, 각 클래스를 동일한 비중으로 고려한다면 macro 평균이 좋다.

# F1 스코어(F1 Score) ***
from sklearn.metrics import f1_score
f1 = f1_score(y_true, y_pred, average='macro')  # average= micro, macro, weighted
print("F1 스코어:", f1)
f1 = f1_score(y_true_str, y_pred_str, average='macro')
print("F1 스코어:", f1)

---

📌 정확도

• 다중분류이지만 정확도를 구하는 방법은 동일하다.

  accuracy_score 를 임포트하여 (실제값, 예측값) 을 배치한다.

---

📌 ROC - AUC ( * 중요 ! )

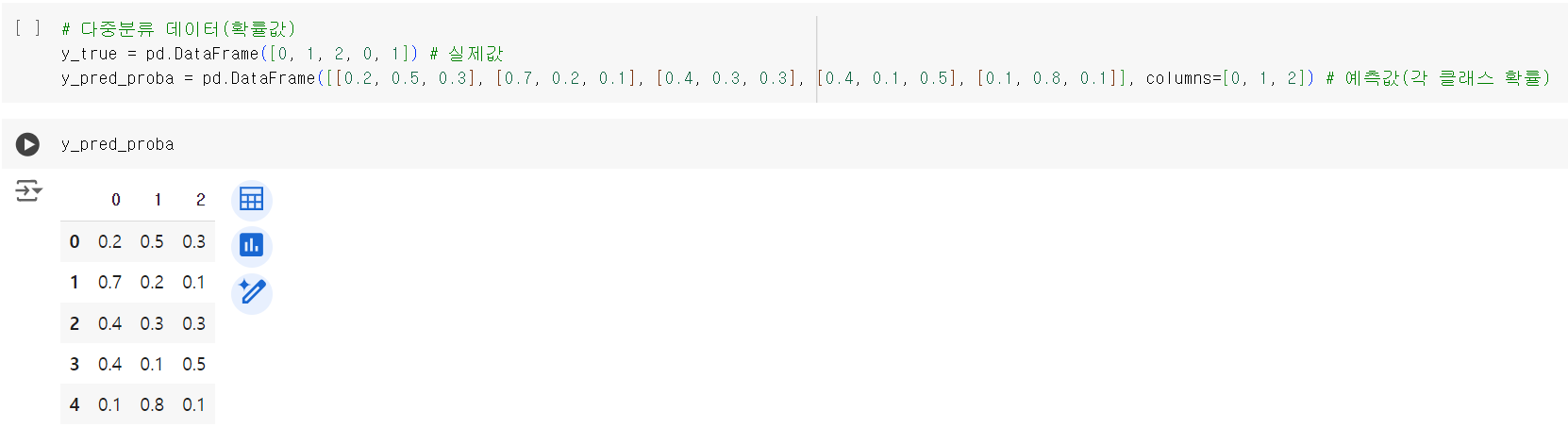
# 다중분류 데이터(확률값)
y_true = pd.DataFrame([0, 1, 2, 0, 1]) # 실제값
y_pred_proba = pd.DataFrame([[0.2, 0.5, 0.3], [0.7, 0.2, 0.1], [0.4, 0.3, 0.3], [0.4, 0.1, 0.5], [0.1, 0.8, 0.1]], columns=[0, 1, 2]) # 예측값(각 클래스 확률)
y_pred_proba

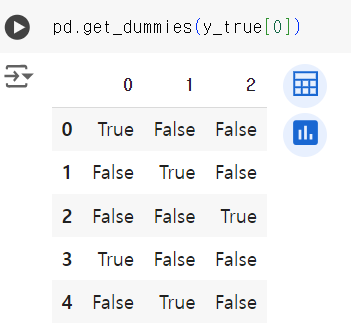
# 원 핫 인코딩
pd.get_dummies(y_true[0])

• 다중분류 시 ROC - AUC 를 구하기 위해서는 ovo 와 ovr 중 인자 선택을 해줘야 한다.

  ovo : one-vs-one (일대일) 을 의미하며 가능한 모든 클래스 쌍 조합의 평균 acu 를 계산,
  average = 'macro' 로 설정했을 때 클래스 불균형에 민감하지 않다.
  ovr : one-vs-rest (일대나머지) 를 의미하며 나머지에 대한 각 클래서 auc 를 계산,
  클래스 불균형이 'rest'에 영향을 미치기 때문에 average = 'macro'로 설정해도 클래스 불균형에 민감하다.

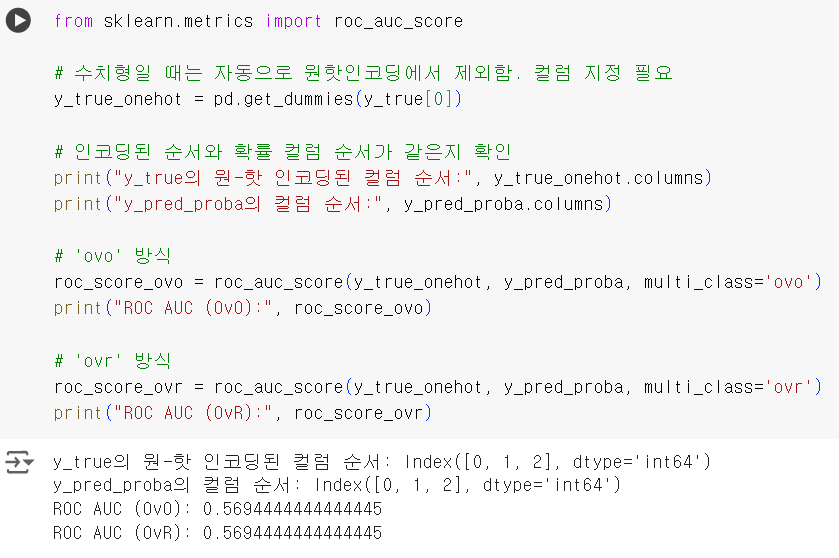
from sklearn.metrics import roc_auc_score
# 수치형일 때는 자동으로 원핫인코딩에서 제외함. 컬럼 지정 필요
y_true_onehot = pd.get_dummies(y_true[0])
# 인코딩된 순서와 확률 컬럼 순서가 같은지 확인
print("y_true의 원-핫 인코딩된 컬럼 순서:", y_true_onehot.columns)
print("y_pred_proba의 컬럼 순서:", y_pred_proba.columns)
# 'ovo' 방식
roc_score_ovo = roc_auc_score(y_true_onehot, y_pred_proba, multi_class='ovo')
print("ROC AUC (OvO):", roc_score_ovo)
# 'ovr' 방식
roc_score_ovr = roc_auc_score(y_true_onehot, y_pred_proba, multi_class='ovr')
print("ROC AUC (OvR):", roc_score_ovr)

# 다중분류 데이터(확률값)
y_true_str = pd.DataFrame(['A', 'B', 'C', 'A', 'B']) # 실제값
y_pred_proba = pd.DataFrame([[0.2, 0.5, 0.3], [0.7, 0.2, 0.1], [0.4, 0.3, 0.3], [0.4, 0.1, 0.5], [0.1, 0.8, 0.1]], columns=['A', 'B', 'C']) # 예측값(각 클래스 확률)
from sklearn.metrics import roc_auc_score
# 원핫인코딩
y_true_onehot = pd.get_dummies(y_true_str)
# 인코딩된 순서와 확률 컬럼 순서가 같은지 확인
print("y_true의 원-핫 인코딩된 컬럼 순서:", y_true_onehot.columns)
print("y_pred_proba의 컬럼 순서:", y_pred_proba.columns)
# 'ovo' 방식
roc_score_ovo = roc_auc_score(y_true_onehot, y_pred_proba, multi_class='ovo')
print("ROC AUC (OvO):", roc_score_ovo)
# 'ovr' 방식
roc_score_ovr = roc_auc_score(y_true_onehot, y_pred_proba, multi_class='ovr')
print("ROC AUC (OvR):", roc_score_ovr)

---

📌 참고

1. 다중분류 확률의 컬럼명 확인
   • pred_proba 의 결과값이 배열 형태로 되어있어 컬럼명이 없음.
   • 확인하는 방법 : model.classes_

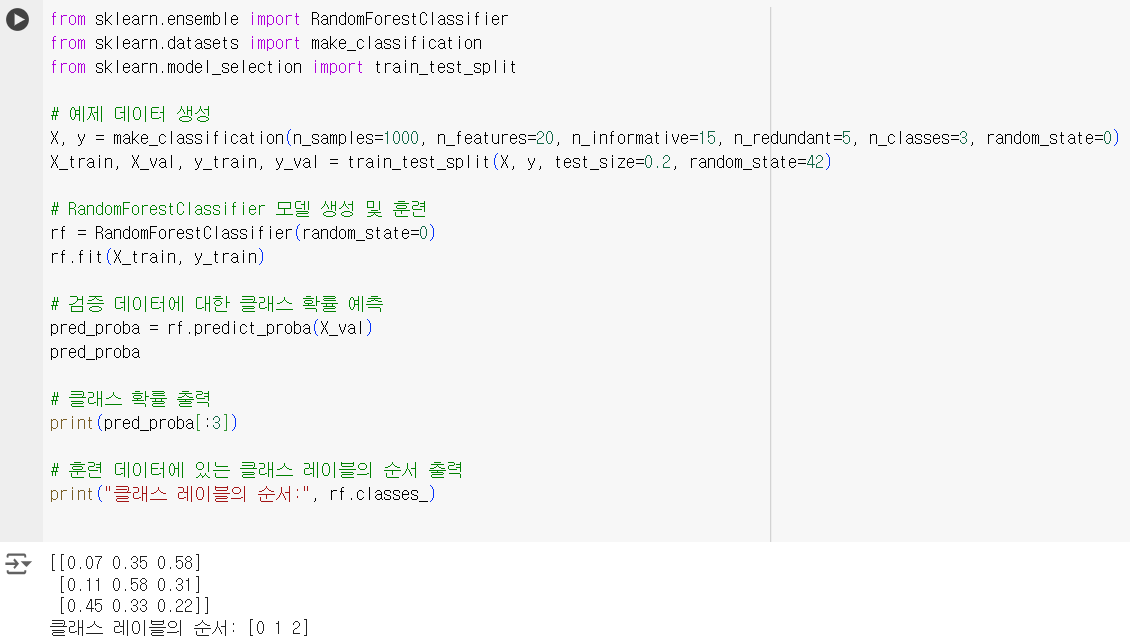
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
# 예제 데이터 생성
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, n_classes=3, random_state=0)
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2, random_state=42)
# RandomForestClassifier 모델 생성 및 훈련
rf = RandomForestClassifier(random_state=0)
rf.fit(X_train, y_train)
# 검증 데이터에 대한 클래스 확률 예측
pred_proba = rf.predict_proba(X_val)
pred_proba
# 클래스 확률 출력
print(pred_proba[:3])
# 훈련 데이터에 있는 클래스 레이블의 순서 출력
print("클래스 레이블의 순서:", rf.classes_)

---

2. 다중분류 확률값을 데이터프레임으로 만들기
   • 예측한 결과를 제출용 파일로 만든다면, 각 클래스에 대한 확률을 각각의 컬럼으로 만들어야 함.
   • 예를 들어, 클래스가 A, B, C 세 가지라면 A에 대한 확률, B, C 에 대한 확률을 각각의 컬럼으로 생성

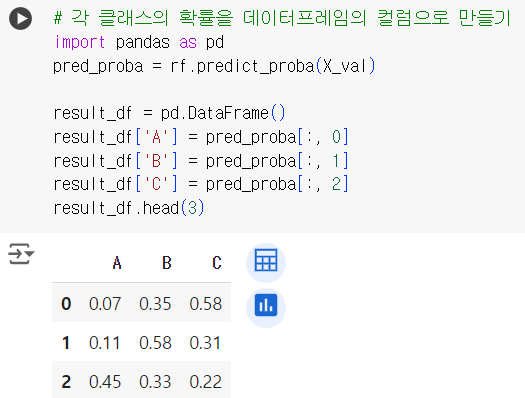
# 각 클래스의 확률을 데이터프레임의 컬럼으로 만들기
import pandas as pd
pred_proba = rf.predict_proba(X_val)
result_df = pd.DataFrame()
result_df['A'] = pred_proba[:, 0]
result_df['B'] = pred_proba[:, 1]
result_df['C'] = pred_proba[:, 2]
result_df.head(3)

---

📌 회귀 평가지표

# 회귀 데이터
import pandas as pd
y_true = pd.DataFrame([0, 2, 5, 2, 4, 4, 7, 10]) # 실제값
y_pred = pd.DataFrame([1.14, 2.53, 4.87, 3.08, 4.21, 5.53, 7.51, 10.32]) # 예측값

---

📌 MAE (Mean Absolute Error)

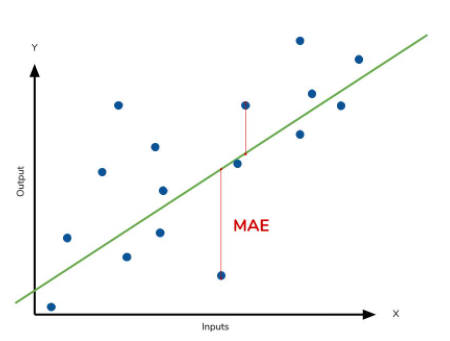
• 평균 절대 오차

  

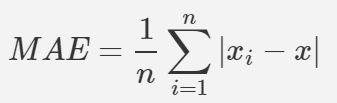
• 실제 값과 예측 값의 차이를 절대값으로 변환하여 평균한 값.
  즉, 모든 오차의 절대값을 취한 평균이 된다.

  MAE는 △X (△X (error) = xi-x / xi - Prediction value , x ; real value) 의 절대값을 취하여
  에러의 크기가 그대로 반영이되는 지표이다.

  그렇기 때문에 예측 결과물의 에러가 10이 나온것이 5로 나온것 보다 2배가 나쁜 도메인에서 쓰기 적합하다.
  이상치(abnormal value)가 많을때 사용하면 용이하다.

  에러의 크기가 그대로 반영되기때문에 수치가 낮을수록 정확성이 높다는것으로 생각하면 된다.
  (실제값과 예측값의 에러가 낮다 -> 모델이 근사적으로 일치하는 모델이 된다)

• 코드

from sklearn.metrics import mean_absolute_error
mean_absolute_error(y_test,y_pred)

+)

# MAE(Mean Absolute Error)
from sklearn.metrics import mean_absolute_error
mae = mean_absolute_error(y_true, y_pred)
print("MAE:", mae)

---

📌 MSE (Mean Squared Error)

• 실제 값과 예측 값의 차이를 제곱하여 평균한 값.

  MSE는 △X (△X (error) = xi-x / xi - Prediction value , x ; real value) 의 넓이의 합의 평균

  특이값이 존재하면 수치가 많이 늘어난다 (제곱하기 때문에)
  통계적 추정의 정확성에 대한 질적인 척도로 수치가 작을수록 정확성이 높은것으로 판단한다.

• 코드

from sklearn.metrics import mean_squared_error
mean_squared_error(y_test, y_pred)

+)

# MSE(Mean Squared Error)
from sklearn.metrics import mean_squared_error
mse = mean_squared_error(y_true, y_pred)
print("MSE:", mse)

---

📌 RMSE (Root Mean Squared Error) ( * 중요 ! )

• MSE 값은 Error의 제곱의 평균으로 실제 Error보다 큰 Error들의 평균을 가지는 특성이 있다.
  그렇기 때문에 MSE값에 √ root를 씌워 RMSE 값을 사용하게 된다. (정밀도의 개념)

• MAE와 MSE의 장점을 모두 가지고 있다.

  Error에 제곱하여 루트N으로 나누게 되어 가중치는 높아진다. 다시말해 큰 Error값에 대해 패널티를 크게준다.
  즉 MSE보다 RMSE가 더 RUBUST하다고 말할수 있다.
  Error 손실이 기하급수적으로 올라가는 상황에서 자주 사용하게 된다.
  (머신러닝에서 specific 한 value에 영향을 덜 받기 위해 자주 사용.)
  RMSE값이 적을 수록 더 좋은 성능이라고 평가할 수 있다.

• 코드

import numpy as np
from sklearn.metrics import mean_squared_error
MSE = mean_squared_error(y_test, y_pred)
np.sqrt(MSE) 
# sklearn 은 mse만 제공하기 때문에 rmse는 직접 만들어 써야한다.

# RMSE(Root Mean Squared Error) ***
from sklearn.metrics import mean_squared_error
mse = mean_squared_error(y_true, y_pred)
rmse = mse ** 0.5
print("RMSE:", rmse)

---

📌 결정 계수 (R-squared) ( * 중요 ! )

• R2 (R-squared) - 분산기반 예측 성능 평가

• RMSE는 에러의 크기에 대한 정보는 주지만, 실제 데이터 값의 크기의 정보는 주지 않는다.

  즉 RMSE의 값이 같더라도 , 데이터 값의 크기가 서로 다르면 성능은 다르게 평가되어야 하는데
  이 때 사용하는것이 R2 평가 모델이다.

  에러의 크기(주로 MSE)를 데이터의 크기(주로 데이터의 분산데이터)로 선택하여 나누어준다.
  R2의 성능은 1에 가까울 수록 좋은 성능을 나타낸다.

• 코드

from sklearn.metrics import r2_score
r2 = r2_score(y, lr.predict(x_2))

+)

# 결정 계수(R-squared) ***
from sklearn.metrics import r2_score
r2 = r2_score(y_true, y_pred)
print("결정 계수:", r2)

---