---

개요

가설검정

---

📌 단일 표본 검정

나커피 유튜버는 최근 판매되는 "합격 원두(dark)" 상품의 실제 무게를 조사하였다.
제조사는 "합격 원두(dark)"의 무게를 120g라고 표기하였다.
나커피 유튜버는 이 주장이 사실인지 확인하기 위해 상품의 무게를 측정하였다.
다음은 30개의 상품 샘플의 무게 측정 결과다.
이 측정 결과를 바탕으로 제조사의 주장인 상품의 무게(120g)가 사실인지 검정해보시오.
(데이터는 정규분포를 따른다고 가정한다.)

import pandas as pd
df = pd.DataFrame({
    '무게':[119, 121, 121, 119, 125, 115, 121, 118, 117, 127,
           123, 129, 119, 124, 114, 126, 122, 124, 121, 116,
           123, 123, 127, 118, 122, 117, 124, 125, 123, 121],
})

• 귀무가설 : μ = μ0, "합격 원두(dark)" 상품의 평균 무게는 120g 이다.
• 대립가설 : μ ≠ μ0, "합격 원두(dark)" 상품의 평균 무게는 120g이 아니다.

+)

• μ : 현재 조사하려는 상품의 실제 평균 무게
• μ0 : 제조사가 주장하는 상품의 평균 무게(120g)

---

📌 기본 (정규분포를 따를 때)

• 단일 표본 검정
  stats.ttest_1samp(data, 기댓값)

# 단일표본검정
from scipy import stats
print(stats.ttest_1samp(df['무게'], 120))
# 검정통계량 2.153
# p - value : 0.039 = 귀무가설 기각, 대립가설 채택 (0.05보다 작기 때문)

• 대립가설 : μ ≠ μ0, "합격 원두(dark)" 상품의 평균 무게는 120g이 아니다.

+) 참고

---

alternative = '' (옵션 : 양측(two-sided), 크기 비교(greater, less))

1. 양측 검정

# 대립가설: 합격 원두(dark)" 상품의 평균 무게는 120g 아니다.
# alternative = 'two-sided' / alternative : 기본값 (양측검정 파라미터)
print(stats.ttest_1samp(df['무게'], 120, alternative = 'two-sided'))
# p - value : 0.039 = 귀무가설 기각, 대립가설 채택 (0.05보다 작기 때문)

2. ~보다 크다

# 대립가설: 합격 원두(dark)" 상품의 평균 무게는 120g 보다 크다
# alternative = 'greater' / 단측 검정 (~보다 크다)
print(stats.ttest_1samp(df['무게'], 120, alternative = 'greater'))
# p - value : 0.0198 = 귀무가설 기각, 대립가설 채택 (0.05보다 작기 때문)

3. ~보다 작다

# 대립가설: 합격 원두(dark)" 상품의 평균 무게는 120g 보다 작다
# alternative = 'less' / 단측 검정 (~보다 작다)
print(stats.ttest_1samp(df['무게'], 120, alternative = 'less'))
# p - value : 0.98 = 귀무가설 채택, 대립가설 기각 (0.05보다 크기 때문)

---

📌 심화 (정규분포를 따르지 않을 때)

# 데이터 (정규성에 만족하지 않게 변경)
import pandas as pd
df = pd.DataFrame({
    '무게':[219, 121, 121, 119, 125, 115, 121, 118, 117, 127,
           123, 129, 119, 124, 114, 126, 122, 124, 121, 116,
           123, 123, 127, 118, 122, 117, 124, 125, 123, 121],
})

1. 샤피로 검정 : 정규성을 확인하는 검정
   stats.shapiro(data)

# Shapiro-Wilk(샤피로-윌크) 정규성 검정
from scipy import stats
stats.shapiro(df['무게'])
# p - value : 0.00000000022 > 대립가설(정규 분포를 따르지 않는다.) 채택

+)

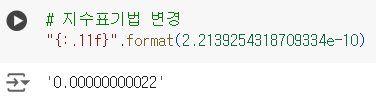
# 지수표기법 변경
"{:.11f}".format(2.2139254318709334e-10)

2. 윌콕슨 검정 (비모수 검정) : 정규 분포를 따르지 않을 때
   stats.wilcoxon(data - 기댓값, alternative = '옵션')

# Wilcoxon(윌콕슨)의 부호 순위 검정 수행
# 대립가설에 해당하는(~보다 작다) 옵션('less') 넣기
stats.wilcoxon(df['무게'] - 120, alternative = 'less')
# p - value : 0.98 > 귀무가설 채택

---

📌 대응 표본 검정

퇴딴 크리에이터는 수험생의 점수 향상을 위해 새로운 교육 프로그램을 도입했다.
도입 전과 도입 후의 점수 차이를 확인하기 위해 동일한 수험생의 점수를 비교했다.
다음은 교육 전과 후의 점수 데이터이다.
새로운 교육 프로그램이 효과가 있는지 검정하시오.
(데이터는 정규분포를 따른다고 가정한다.)

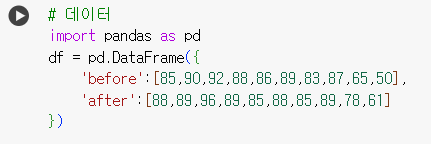
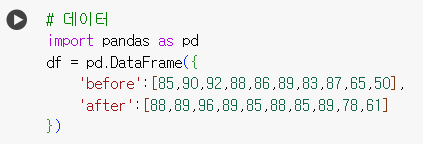
# 데이터
import pandas as pd
df = pd.DataFrame({
    'before':[85,90,92,88,86,89,83,87,65,50],
    'after':[88,89,96,89,85,88,85,89,78,61]
})

μd = (before – after)의 평균

• 귀무가설: μd ≥ 0, 새로운 교육 프로그램은 효과가 없다.
• 대립가설: μd < 0, 새로운 교육 프로그램은 효과가 있다.

---

📌 기본 (정규분포를 따를 때)

• 대응 표본 검정
  stats.ttest_rel(data1, data2)

# 대응표본검정
from scipy import stats
stats.ttest_rel(df['before'], df['after'], alternative = 'less')

+) data1, data2 의 순서에 상관없이 같은 결과가 나온다.

# 대응표본검정
from scipy import stats
stats.ttest_rel(df['after'], df['before'], alternative = 'greater')

---

📌 심화 (정규분포를 따르지 않을 때)

1. 샤피로 검정

# Shapiro-Wilk(샤피로-윌크) 정규성 검정
df['diff'] = df['after'] - df['before']
from scipy import stats
stats.shapiro(df['diff'])
# 대립가설 채택 :정규분포를 따르지 않는다. 

2. 윌콕슨 검정 (비모수 검정)

# Wilcoxon(윌콕슨)의 부호 순위 검정 수행
from scipy import stats
stats.wilcoxon(df['after'], df['before'], alternative = 'greater')
# Wilcoxon(윌콕슨)의 부호 순위 검정 수행 (diff)
stats.wilcoxon(df['diff'], alternative = 'greater')
# p - value : 0.02 > 대립가설 채택

---

📌 독립 표본 검정

다음은 빅데이터 분석기사 실기 시험 점수이다.
A그룹과 B그룹의 평균 점수가 차이가 있는지 유의수준 0.05하에서 가설 검정하시오.
(데이터는 정규분포를 따르고 분산이 동일하다고 가정한다.)

# 데이터
# 대응표본 검정은 사전, 사후를 비교하기 때문에 데이터의 길이가 같아야 하지만,
# 독립표본 검정에서는 데이터의 길이가 달라도 된다.
A = [85, 90, 92, 88, 86, 89, 83, 87,
     84, 50, 60, 39, 28, 48, 38, 28]
B = [82, 82, 88, 85, 84, 74, 79, 69,
     78, 76, 85, 84, 79, 89]

• 귀무가설(H0): 그룹별 시험 평균 점수는 차이가 없다. (μ1 = μ2)
• 대립가설(H1): 그룹별 시험 평균 점수는 차이가 있다. (μ1 ≠ μ2)

---

📌 기본 (정규분포를 따르고 등분산일 때)

• 독립 표본 검정
  stats.ttest_ind(처리집단, 대조집단)
  여기서 처리집단은 어떤 변화를 준 집단, 대조집단은 아무것도 하지 않은 원래 집단

# 독립표본검정
from scipy import stats
stats.ttest_ind(A, B) # ttest_ind(처리집단, 대조집단)
# 대립가설 채택 : 차이가 있다.

---

# 독립표본검정(less)
stats.ttest_ind(A, B, equal_var = True, alternative = 'less') 

# 독립표본검정(greater)
stats.ttest_ind(A, B, equal_var = True, alternative = 'greater') 

---

📌 심화 (정규분포를 따르지 않고 분산이 동일하지 않을 때)

# 데이터
import pandas as pd
A = [85, 90, 92, 88, 86, 89, 83, 87,
     84, 50, 60, 39, 28, 48, 38, 28]
B = [82, 82, 88, 85, 84, 74, 79, 69,
     78, 76, 85, 84, 79, 89]

1. 샤피로 검정

# Shapiro-Wilk(샤피로-윌크) 정규성 검정
from scipy import stats
print(stats.shapiro(A)) # p - value = 0.004 : 정규성을 만족하지 않는다.
print(stats.shapiro(B)) # p - value = 0.739 : 정규성을 만족한다.

2. 레빈 검정 (등분산성 검정)

# Levene(레빈) 등분산 검정 (귀무가설: 분산이 동일하다)
stats.levene(A, B) # 대립가설 채택 : 분산이 동일하지 않다.

3. 독립 표본 검정

equal_var = False : 두 집단의 분산이 다를 때 넣어주는 옵션

# 두 집단의 분산이 다르다 (equal_var = False)
stats.ttest_ind(A, B, equal_var = False) 

# 독립표본검정
stats.ttest_ind(A, B, equal_var = False, alternative = 'less')
# 대립가설 채택

4. 만 휘트니 유 검정

• mannwhitneyu(data1, data2, alternative = '')
  정규분포를 따르지 않고 두 집단의 분산이 다를 때

# Mann-Whitney U(만-휘트니 유) 검정
stats.mannwhitneyu(A, B, alternative = 'less')
# 귀무가설 채택

---