---

개요

가설검정

• 귀무가설과 대립가설

• 검정 결과

• 가설검정 프로세스

• T - test

• 단일 표본 검정

• 대응 표본 검정

• 독립 표본 검정

---

📌 가설 검정

---

📌 모집단과 표본

모집단 : 연구 대상이 되는 전체 집단
표본 : 모집단의 일부

---

📌 귀무가설과 대립가설

귀무가설 : 기존에 알려진 사실, 효과나 차이가 없다.
대립가설 : 연구자(분석가)가 입증하려는 사실, 효과나 차이가 있다.

---

📌 검정 결과

검정 통계량 : 주어진 데이터와 귀무가설 간의 차이를 통계적으로 나타내는 값
p - value : 유의수준

• 유의수준보다 작으면 귀무가설을 기각하고, 대립가설 채택
• 유의수준보다 크면 귀무가설을 기각하지 못하고, 귀무가설 채택

---

📌 가설검정 프로세스

1. 통계적 가설 설정 : 귀무가설 과 대립가설
2. 유의수준 결정 : 0.05 (보통의 값)
3. 검정 통계량 및 p - value (유의확률) 계산
4. 결과 도출

---

📌 T - test

T - 검정

---

📌 단일 표본 검정

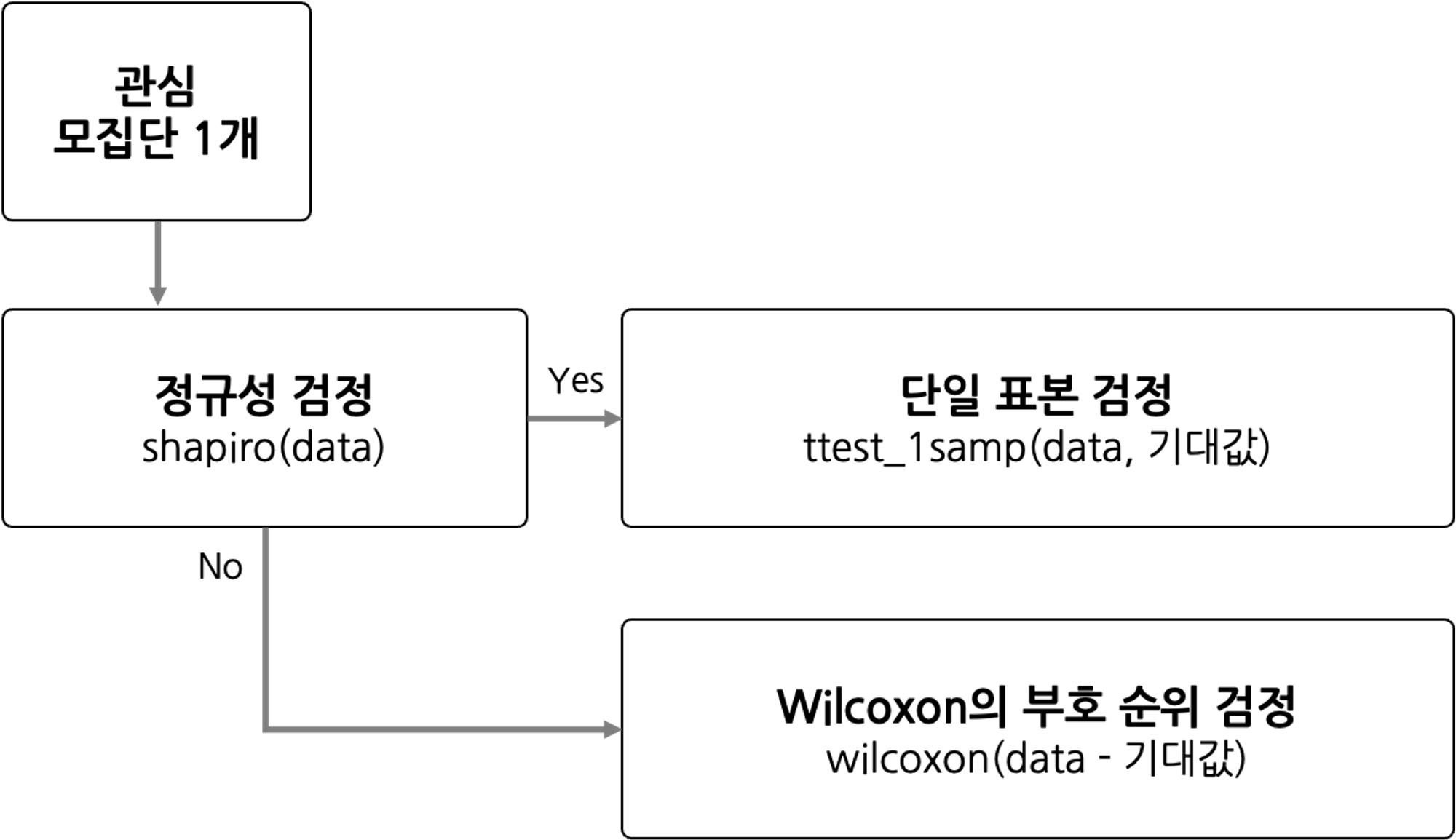
모집단이 1개일 경우, 한 그룹에 대한 검정 프로세스

1. stats.shapiro(data) :

   # 정규성을 판단하는 샤피로 검정
   귀무가설(H0) : 주어진 데이터 샘플은 정규분포를 따른다.
   대립가설(H1) : 주어진 데이터 샘플은 정규분포를 따르지 않는다.

   • p - value : 0.05 초과 (귀무가설; 정규분포를 따른다. 채택)
     정규성이 있다 > 단일 표본 검정 시행
   • p - value : 0.05 이하 (대립가설; 정규분포를 따르지 않는다. 채택)
     정규성이 없다 > 윌콕슨의 부호 순위 검정 시행

2. ttest_1samp(data, 기댓값) : 정규성을 따르는 1개 모집단의 T 검정

   • p - value : 0.05 초과 (귀무가설 채택)
   • p - value : 0.05 이하 (대립가설 채택)

3. wilcoxon(data - 기댓값) : 정규성을 따르지 않는 1개 모집단의 T 검정

   • p - value : 0.05 초과 (귀무가설 채택)
   • p - value : 0.05 이하 (대립가설 채택)

---

📌 대응 표본 검정

모집단이 2개일 경우, 같은 그룹에 대한 검정 프로세스
사건의 전, 후 차이가 있는지 볼 때 주로 사용 !

1. stats.shapiro(diff) : diff = data1 - data2 (두 집단의 차이)

   # 정규성을 판단하는 샤피로 검정
   귀무가설(H0) : 주어진 데이터 샘플은 정규분포를 따른다.
   대립가설(H1) : 주어진 데이터 샘플은 정규분포를 따르지 않는다.

   • p - value : 0.05 초과 (귀무가설; 정규분포를 따른다. 채택)
     정규성이 있다 > 대응 표본 검정 시행
   • p - value : 0.05 이하 (대립가설; 정규분포를 따르지 않는다. 채택)
     정규성이 없다 > 윌콕슨의 부호 순위 검정 시행

2. ttest_rel(data1, data2) : 정규성을 따르는 2개 모집단의 T 검정

   • p - value : 0.05 초과 (귀무가설 채택)
   • p - value : 0.05 이하 (대립가설 채택)

3. wilcoxon(data1, data2) : 정규성을 따르지 않는 2개 모집단의 T 검정

   • p - value : 0.05 초과 (귀무가설 채택)
   • p - value : 0.05 이하 (대립가설 채택)

---

📌 독립 표본 검정

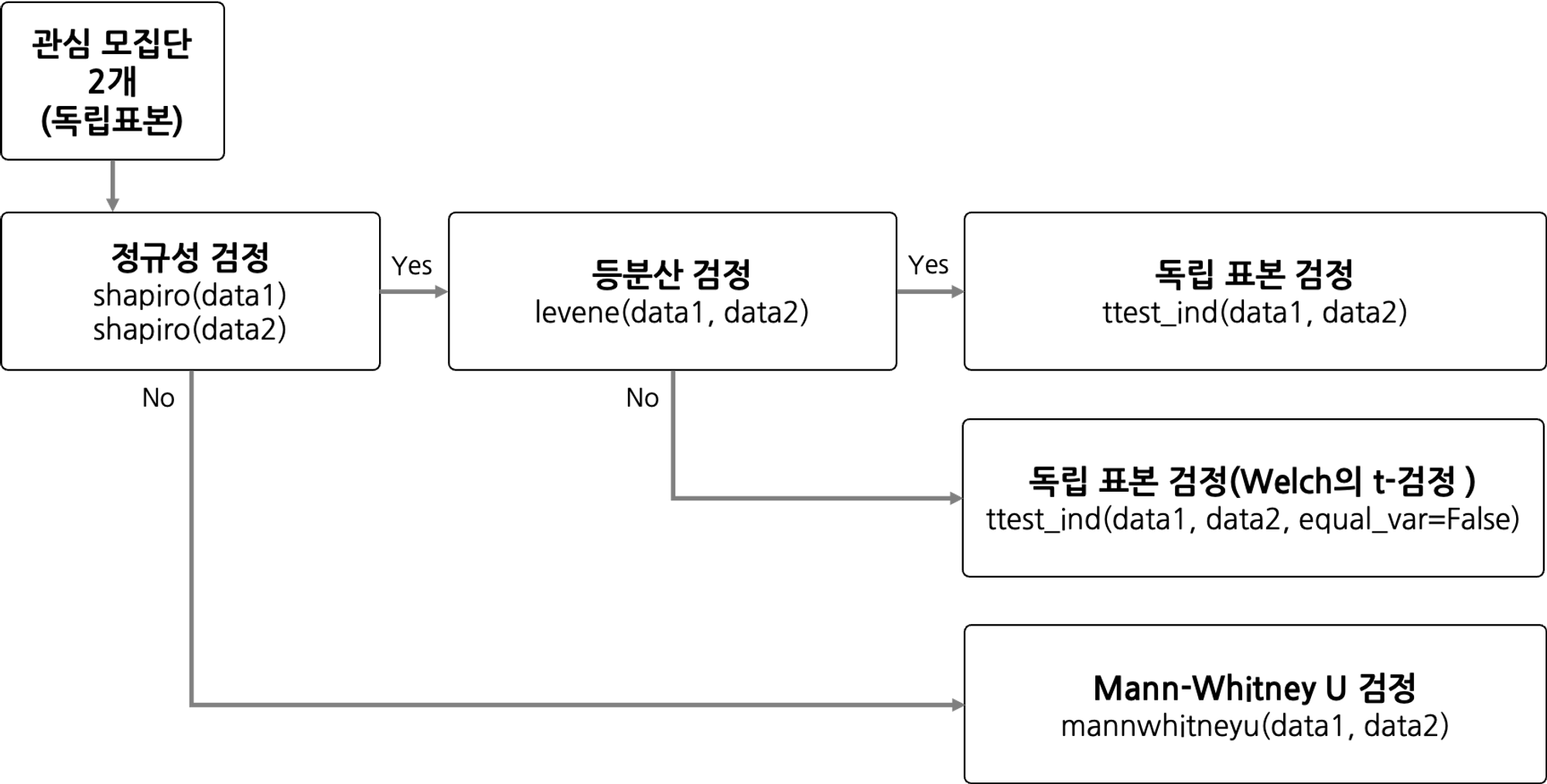
모집단이 2개일 경우, 서로 다른 그룹에 대한 검정 프로세스

1. stats.shapiro(data1) , stats.shapiro(data2) :
   data1, data2 (각 집단이 정규성을 만족하는지 확인)

   # 정규성을 판단하는 샤피로 검정
   귀무가설(H0) : 주어진 데이터 샘플은 정규분포를 따른다.
   대립가설(H1) : 주어진 데이터 샘플은 정규분포를 따르지 않는다.

   • p - value : 0.05 초과 (귀무가설; 정규분포를 따른다. 채택)
     정규성이 있다 > 등분산 검정 시행
   • p - value : 0.05 이하 (대립가설; 정규분포를 따르지 않는다. 채택)
     정규성이 없다 > 만 위트니 유 검정 시행

2. levene(data1, data2) : 정규성을 따르는 2개 모집단의 등분산 검정 (레빈 검정)

   # 등분산성을 판단하는 레빈 검정
   귀무가설(H0) : 주어진 데이터 샘플은 분산이 동일하다.
   대립가설(H1) : 주어진 데이터 샘플은 분산이 동일하지 않다.

   • p - value : 0.05 초과 (귀무가설 채택)
   • p - value : 0.05 이하 (대립가설 채택)

3. ttest_ind(data1, data2) :
   정규성을 따르고 등분산성이 있는 2개 모집단의 T 검정

   • p - value : 0.05 초과 (귀무가설 채택)
   • p - value : 0.05 이하 (대립가설 채택)

4. ttest_ind(data1, data2, equal_var = False) :
   정규성을 따르고 등분산성이 없는 2개 모집단의 T 검정

   • p - value : 0.05 초과 (귀무가설 채택)
   • p - value : 0.05 이하 (대립가설 채택)

5. mannwhitneyu(data1, data2) :
   정규성을 따르지 않는 2개 모집단의 T 검정

   • p - value : 0.05 초과 (귀무가설 채택)
   • p - value : 0.05 이하 (대립가설 채택)

---