개요
<통계학>
데이터 분석 및 과학을 위한 핵심 통계지식 학습
PYTHON 활용 :
통계적 가설검증,회귀(예측),분류(지도학습),클러스터링(비지도학습)에 대한 이해
📌 1회차 요약
-
python은 데이터의 종류에 따라 관련된 계산을 어떤식으로 수행할 지 결정
-
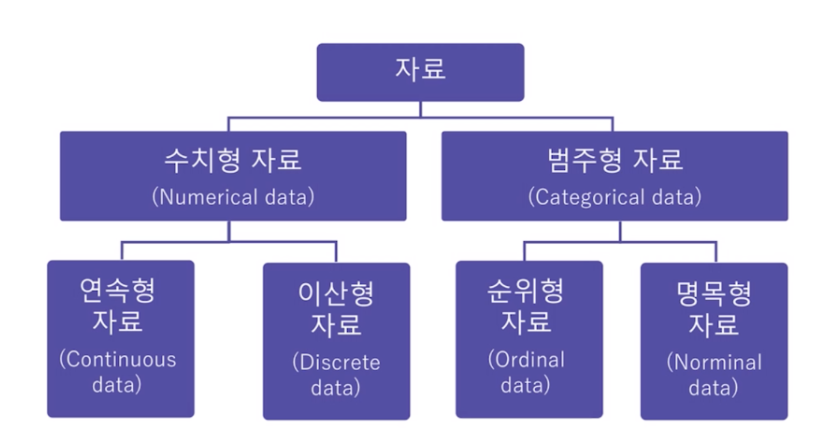
데이터 종류 : 대표적으로 수치형, 범주형 데이터
-
데이터 대표값 : 평균, 중간값, 최빈값
데이터 분포를 보다 명확히 파악하기 위해 편차, 분산, 표준편차 학습 -
편차는 그 합이 0 으로 분포를 확인할 수 없다.
→ 음수값을 없애기 위해 제곱을 취해주는 분산의 개념이 도입
→ 분산은 제곱값이라 단위가 다르기 때문에 제곱근(루트)을 씌워 단위를 맞춤
→ 표준편차 -
무수히 많은 데이터를 대상으로 효과적인 통계분석을 위해 표본추출이 이뤄지고 있다.
-
모집단은 어떤 데이터 집합을 구성하는 전체이고, 표본은 그 중 일부(부분집합)
-
표본의 분포를 가지고 모집단의 분포를 추정하며,
해당 과정에서 무수히 많은 경우의 수의 표본이 생성될 수 있다. -
표본 크기가 충분히 크다면 어떤 분포에서도 표본평균이 정규분포를 따른다는 것
→ 중심극한정리 -
정규분포는 종 모양을 띄고 있으며, 분포는 좌우 대칭의 형태입니다.
평균치에서 그 확률이 가장 높다. -
정규분포에서 평균 0, 분산 1을 가지는 경우, 이를 표준정규분포라고 한다.
데이터분석시 이를 표준화라고 부름 -
데이터분석시 표준화가 필요한 경우 :
머신러닝 모델을 만들 때, 데이터의 범위가 많이 차이나는 경우.
예시) 최근 일주일 접속일수의 1과 결제금액의 1 은 같은 의미가 아니며,
범위가 큰 데이터의 경우 숫자가 가지는 절대치를 잘못 받아들일 수 있어
표준화는 반드시 필요
📌 데이터의 종류
📌 데이터의 종류를 분류해야 하는 이유
데이터를 분석하고 예측할 때
데이터의 생김새에 따라 시각화, 해석, 통계 모델 결정 등에 중요한 역할을 하기 때문 !
| 데이터 종류 | 개념 | 예시 |
|---|---|---|
| 수치형 | 숫자를 이용해 표현할 수 있는 데이터 이산형, 연속형 을 모두 포함하는 개념 | 체중, 신장,사고건수,일 방문자수 |
| 연속형 | 일정 범위 안에서 어떤 값이든 취할 수 있는 데이터 | 체중, 신장 |
| 이산형 | 횟수와 값은 정수형 값만 취할 수 있는 데이터 즉, 소수점의 의미가 없는 데이터를 의미(수치형 데이터와의 차이점) | 사고건수, 일 방문자수 |
| 범주형 | 가능한 범주 안의 값만을 취하는 데이터 = 값이 달라짐에 따라 좋거나 나쁘다고 할 수 없는 데이터 = 명목형 이진형, 순서형 을 모두 포함하는 개념 | 나라, 도시, 혈액형, 성별, 성공여부, 등수 |
| 이진형 | 두개의 값만을 가지는 범주형 데이터의 특수한 경우 / 0과1 / 예/아니오 참/거짓 | 성별, 성공여부 |
| 순서형 | 값들 사이에 분명한 순위가 있는 데이터 | 등수 |
- 데이터 종류는 크게
수치형및범주형으로 나뉜다.
📌 편차, 분산, 표준편차, 표본분포
테이블이 주어졌을 때 이를 살펴보는 가장 기초적인 단계는
각 컬럼의대표값을 구하는 것.
대표값은 평균, 중앙값, 최빈값 등이 될 수 있는데,
대표값만으로는 데이터를 분석했다고 하기 어렵다.
- 평균, 중앙값, 최빈값 등의 대표값들은 데이터의
WHERE(어디에 존재하는가)를 표현해주는 개념
하지만 아래 그래프처럼 평균은 같지만 데이터가 다르게 분포되어 있는지 알기 위해서는
편차, 분산, 표준편차의 개념이 필요하다.
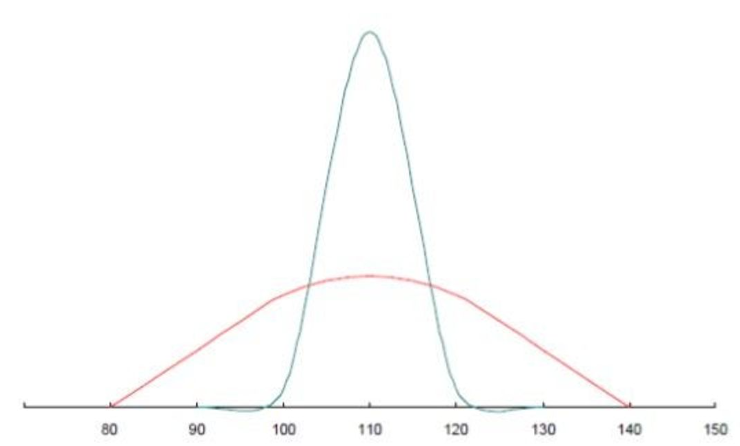
- 편차, 분산, 표준편차는
HOW(어떻게 존재하는가)를 표현해주는 개념
📌 편차
편차(deviation) : 하나의 값에서 평균을 뺀 값 = 평균으로부터 얼마나 떨어져 있는지를 의미
- A 학생의 영어점수: 30점
- B 학생의 영어점수: 70점
- C 학생의 영어점수: 80점
- A,B,C 학생의 평균 영어점수: 60점
> A 학생의 편차: -30
> B 학생의 편차: +10
> C 학생의 편차: +20학생 전체의 편차를 나타내기 위해 각 학생들의 편차를 모두 더하게 되면 0 이 나오는데,
편차로는 반 전체의 점수 분포를 정확히 알 수가 없기에 나온 개념이 분산이다.
📌 분산
분산(variance) : 편차의 합이 0으로 나오는 것을 방지하기 위해 생성된 개념 = 편차 제곱합의 평균
- A 학생의 편차 제곱: (-30)^2 = 900
- B 학생의 편차 제곱: (+10)^2 = 100
- C 학생의 편차 제곱: (+20)^2 = 400
> 편차 제곱합: 1400
> 편차 제곱합의 평균(분산): 1400/3 = 466 분산은 466이지만 점수 값에 제곱을 하게 되면서 그 단위가 달라지게 된다.
실제 데이터가 어느정도로 차이가 있는 지 알기 어렵게 되는 문제를 해결하기 위해
도입된 개념이 표준편차이다.
📌 표준편차
표준편차 : 분산에 제곱근을 씌워준 값 (=원래 단위로 되돌리기 = standard deviation(σ))
466 * 0.5
= 21.5870331449..표준편차는 약 21.6으로 반 전체의 영어점수가 약 20만큼 퍼져(분산되어) 있다.
라고 해석이 가능하다.
📌 모집단, 표본, 표본분포
-
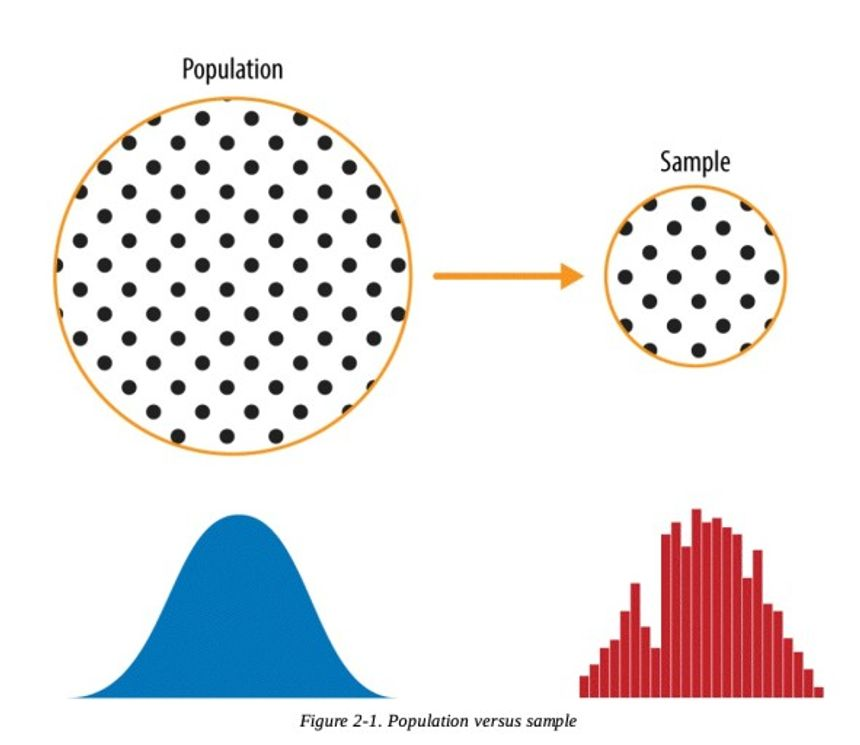
모집단: 어떤 데이터 집합을 구성하는 전체 대상 -
표본: 모집단 중 일부. 모집단의 부분 집합
-
표본 분포: 표본의 분포, 표본이 흩어져 있는 정도, 표본통계량으로부터 얻은 도수분포 -
표준 오차: 표본의 표준편차 = 표본평균의 평균과 모평균의 차이
📌 정규분포, 신뢰구간
📌 정규분포
중심극한정리, 표본을 선정할 때 그 경우의 수가 매우 많고, 경우의 수를 평균내어 모아보면
종 모양의 분포를 띄게 되는데, 이를 정규분포라 한다.
- 정규분포의 특징
- 분포는 좌우 대칭의 형태, 평균치에서 가장 그 확률이 높다.
- 곡선은 각 확률값을 나타내며, 모두 더하면 1이 된다.
- 정규분포는 평균과 분산(퍼진 정도)에 따라 다른 형태를 가진다.
- 평균 0, 분산 1을 가지는 경우,
표준 정규분포라고 한다. (위 그림의 붉은색 그래프)
- 왜 표준 정규분포 ?
-
정규분포 그래프에서 그래프 아래쪽의 영역은 모두 확률.
(전체 경우의 수 중 어떠한 사건이 일어날 경우의 수) -
각각의 그래프는 평균과 분산값에 따라 다르게 그려질 수 있고,
이럴 경우, 확률을 계산할 때 어려움을 겪게 된다.- 이를 통일하기 위해 분포의 평균과 분산값을 통일하는 작업을 하게 되는데,
이를표준화라고 한다.- 표준화 공식 : 확률변수 X 에서 평균 m 을 빼고 표준편차로 나누기
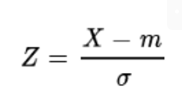
- 표준화 공식 : 확률변수 X 에서 평균 m 을 빼고 표준편차로 나누기
- 이를 통일하기 위해 분포의 평균과 분산값을 통일하는 작업을 하게 되는데,
-
데이터 분석 시 표준화가 필요한 경우 :
머신러닝 모델을 만들 때, 데이터의 범위가 많이 차이나는 경우.
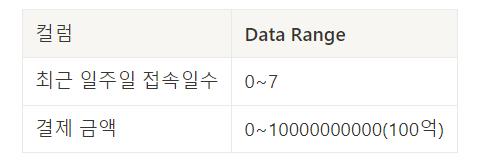
최근 일주일 접속일수의 1과 결제금액의 1은 큰 범위 차이 때문에 같은 의미를 가지지 못한다.
하지만 머신러닝 시, 해당 값의 의미를 같게 받아들이고 처리할 수 있으며, 범위가 큰 데이터의 경우
숫자가 가지는 절대치를 받아들이 수 있어 표준화는 반드시 필요합니다.
- 신뢰 구간, 신뢰 수준
모든 데이터는 표본을 추출하는 순간 불확실성을 가지게 된다.
모집단 전체를 사용하지 않는 한, 결과가 한 끗 차이도 나지 않기는 어렵다.
데이터의 불확실성을 신뢰구간이라는 개념으로 약속
신뢰구간: 특정 범위 내에 값이 존재할것으로 예측되는 영역
(영어점수가 10점에서 90점 사이일 것 같아요)신뢰수준: 실제 모수를 추정하는데 몇 퍼센트의 확률로 신뢰구간이 실제 모수를 포함하게 되는 확률. 주로 95%와 99% 를 이용
(영어점수가 10점에서 90점 사이일에 분포할 확률이 95%)
scipy활용하여 95% 와 99% 신뢰구간 구하기
import scipy.stats as st
import numpy as np
#샘플 데이터 선언
sample1 = [5, 10, 17, 29, 14, 25, 16, 13, 9, 17]
sample2 = [21, 22, 27, 19, 23, 24, 20, 26, 25, 23]
df = len(sample1) - 1 # 자유도 : 샘플 개수 - 1
mu = np.mean(sample1) # 표본 평균
se = st.sem(sample1) # 표준 오차
# 95% 신뢰구간 ( = 95% 신뢰하려면 데이터의 범위가 어떻게 되는지?)
st.t.interval(0.95, df, mu, se) # (10.338733110887336, 20.661266889112664)
# 99% 신뢰구간( = 99% 신뢰하려면 데이터의 범위가 어떻게 되는지?)
st.t.interval(0.99, df, mu, se) # (8.085277068873378, 22.914722931126622)