STATISTICS#2

codataffee·2024년 6월 5일

Statistics

STATISTICS

목록 보기

2/4

개요

<통계학>
데이터 분석 및 과학을 위한 핵심 통계지식 학습

PYTHON 활용 :
통계적 가설검증, 회귀(예측), 분류(지도학습), 클러스터링(비지도학습) 에 대한 이해

📌 2회차 요약

A/B 테스트 : 방법론과 사용되는 통계개념 학습
가설설정, 통계적 의미 해석(P-value), 가설검정(T검정, 카이제곱검정)이 있다.
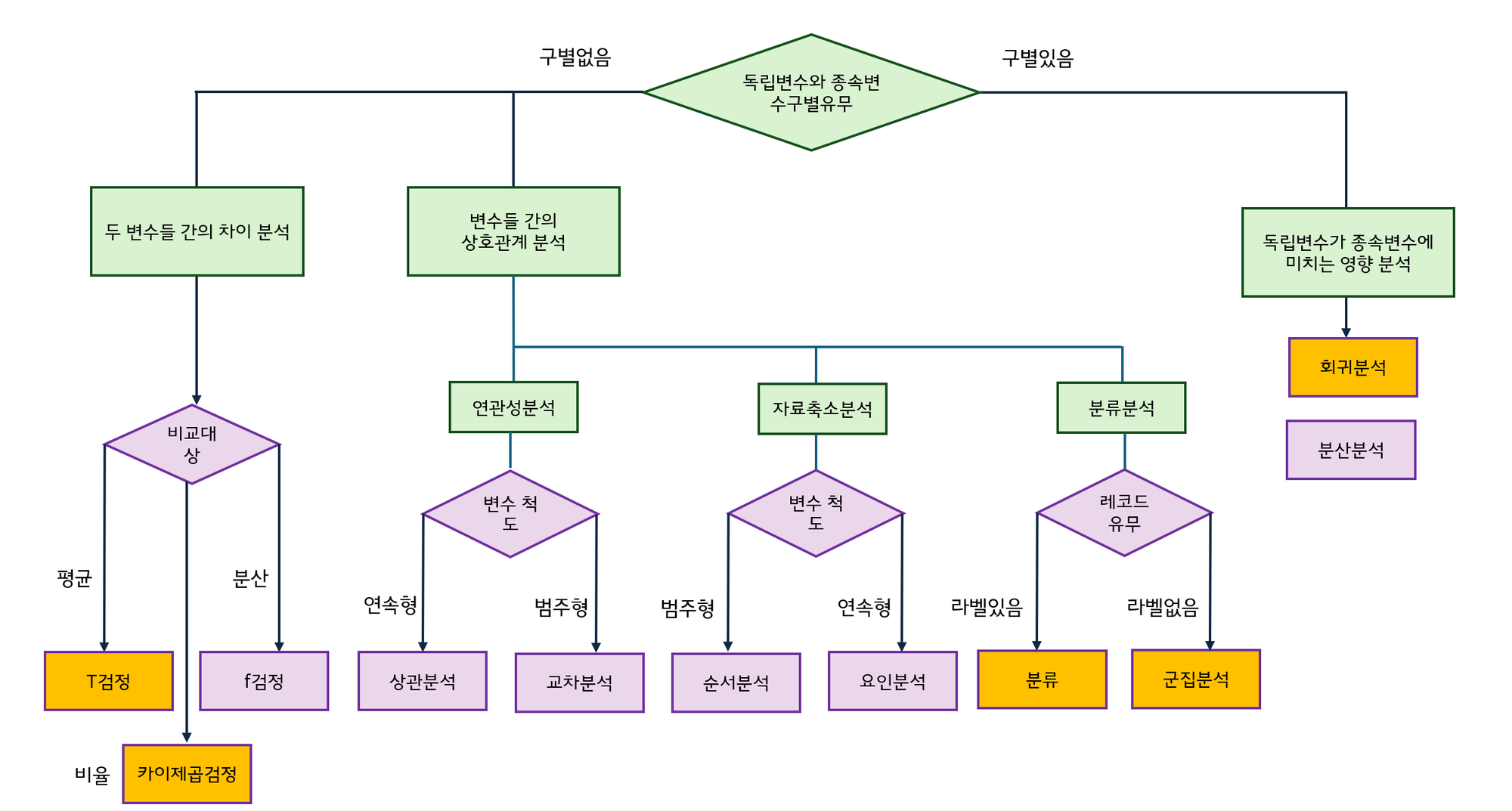
A/B 테스트는 5가지 단계로 진행
현행 데이터 탐색 → 가설 설정 → 유의수준 설정 → 실험 → 해석
귀무가설은 차이가 없거나 의미 있는 차이가 없는 경우의 가설
대립가설은 차이가 있는 경우의 가설
유의수준은 신뢰도의 반대 개념
오류의 허용 범위로 보통 0.05를 사용, 이는 곧 신뢰도 95% 를 의미
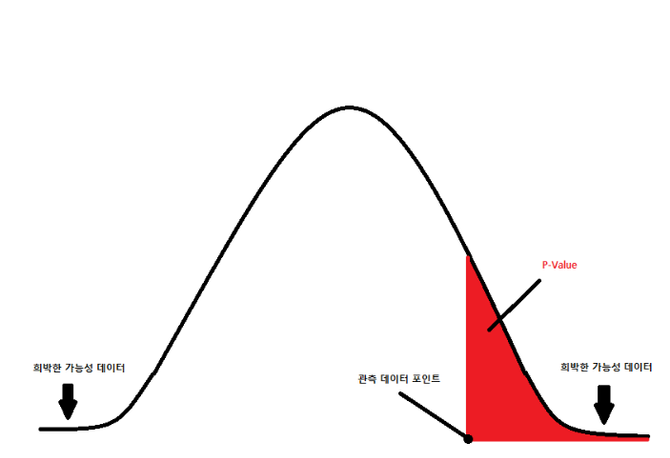
p-value 는 어떠한 사건이 우연하게 발생할 확률
p-value가 0.05 보다 작다
= 우연히 일어났을 가능성이 거의 없다
= 인과관계가 있다고 추정
= 대립가설 채택
python library 를 통해서 검정 진행 실습

📌 통계적 실험

실험설계의 목표 : 어떤 가설의 확인이나 기각

통계적 실험이란?

어떤 목적을 가지고 관찰을 통해 측정값을 얻어내는 것

실험의 목적

통계적 추론을 통해 보다 진실에 가까운 값을 도출하기 위함
✍️
모든 까마귀는 검정색이다.
→ 모든 까마귀가 검정색이 아닐수도 있다?
→ 하지만 전 세계에 있는 까마귀를 모두 확인하는 것은 불가능하다.
→ 통계적 추론을 통해 진실에 가까운 값 도출

✍️
제한된 환경에서의 관찰을 통해 확보된 사실을 바탕으로 제한된 결론을 내리고,
확률적 판단으로 제한된 결론을 내려 진실에 가까운 값 도출

프로세스

가설 수립 → 실험 설계 → 데이터 수집 → 추론 및 결론의 도출

분석 기법 선택

📌 A / B TEST

A / B TEST 란?

두 가지 처리 방법 중 어느 쪽이 더 좋다. 는 것을 입증하기 위해
실험군을 두 그룹으로 나누어 진행하는 실험

버킷 테스트 또는 분할 테스트 라고도 부른다.

테스트 목적

UI/UX 개선 :
서비스에 진입한 방문자의 니즈에 맞지 않는 UI,UX 는 고객 이탈의 가능성이 있다.
고객이 될 수 있었던 방문자를 놓치지 않으려면 A / B 테스트를 통해 개선하는 작업이 중요
전환율 증가 :
A / B 테스트를 통해 무엇이 효과가 있는지 (또는 없는지) 파악하면
전환율 상승에 도움이 된다. (c 배너보다 d 배너의 전환이 더 좋구나!)
매출 증가 :
A / B 테스트를 통해 UX가 개선되면 전환율이 상승할 뿐 아니라,
브랜드에 대한 고객 충성도도 높아지고, 이는 곧 반복 구매로 이어져 매출 증가에 영향

주요 지표

서비스 가입율, 재방문율, CTR(노출 대비 클릭율),
CVR(클릭 대비 전환율, 구매전환율), ROAS(캠페인 비용 대비 캠페인 수익),
eCPM(1,000회 광고 노출당 얻은 수익)

프로세스

A/B 테스트는 크게 다섯가지 단계로 진행 !
다음 챕터에서 단계별로 상세하게 알아보도록 할게요.

현행 데이터 탐색
- 주요 지표를 기준으로 현재 데이터 탐색
가설 설정
- 비즈니스 목표를 달성하는 데 필요한 KPI 정의
- KPI 전환율 증가를 위한 귀무가설, 대립가설 설정
  귀무 가설
  ◦ 통계학에서 처음부터 버릴 것을 예상하는 가설
  ◦ 차이가 없거나 의미 있는 차이가 없는 경우의 가설
  ◦ "새로운 광고배너를 게재해도 기존과 차이가 없을 것이다"
  
  대립 가설
  ◦ 귀무가설에 대립하는 명제
  ◦ "새로운 광고배너를 게재해도 기존과 차이가 있을 것이다(다를 것이다)"
유의수준 설정

귀무가설이 맞을 때 오류를 얼마나 허용할 것인지 기준을 정하는 단계
테스트 설계 및 실행
- 사용자를 대조군과 실험군의 두 그룹으로 분리
- 대조군 그룹에게는 제품이나 서비스의 현재 버전을 보여주고,
  실험군 그룹에게는 새 버전 노출
테스트 결과 분석
- 측정 항목(가설)에 대해 두 그룹의 결과를 분석 (검정통계량 분석)
- 통계적 방법으로 결과를 분석하여 대조군과 실험군 사이의 통계적으로 유의미한 차이가 있는지 확인

✅ A/B 테스트 주의사항

적절한 표본 크기 :
표본의 크기가 충분하지 않으면 유의미한 결과를 얻을 수 없다.
적절한 표본 크기를 결정하고, 그에 맞는 시간과 자원을 투자해야 함
하나의 변수만 변경 :
A / B 테스트에서는 하나의 변수만을 변경해야 한다.
두 가지 이상의 변수를 동시에 변경하면 어떤 변수가 영향을 미쳤는지 파악할 수 없기 때문
무작위성 :
A / B 테스트는 무작위로 선택된 사용자들에게 각각 다른 변수를 적용해야 한다.
적절한 분석 방법 :
A / B 테스트 결과를 해석할 때
가설 검증을 위한 통계적 분석 방법을 선택하고, 유의수준 설정
테스트 결과의 의미 :
A / B 테스트 결과가 통계적으로 유의미하더라도
항상 실제로 의미 있는 결과인지 한번 더 생각해봐야 함
정해진 기간 동안 진행 :
A / B 테스트는 일정 기간 동안 진행
그 기간 동안에만 결과를 수집하고, 분석해야 한다.
너무 짧은 기간 동안에는 결과를 수집하기 어렵고,
너무 긴 기간 동안에는 사용자들의 행동이 변할 가능성이 있어 기간을 잘 정해야 함!

📌 유의수준 설정

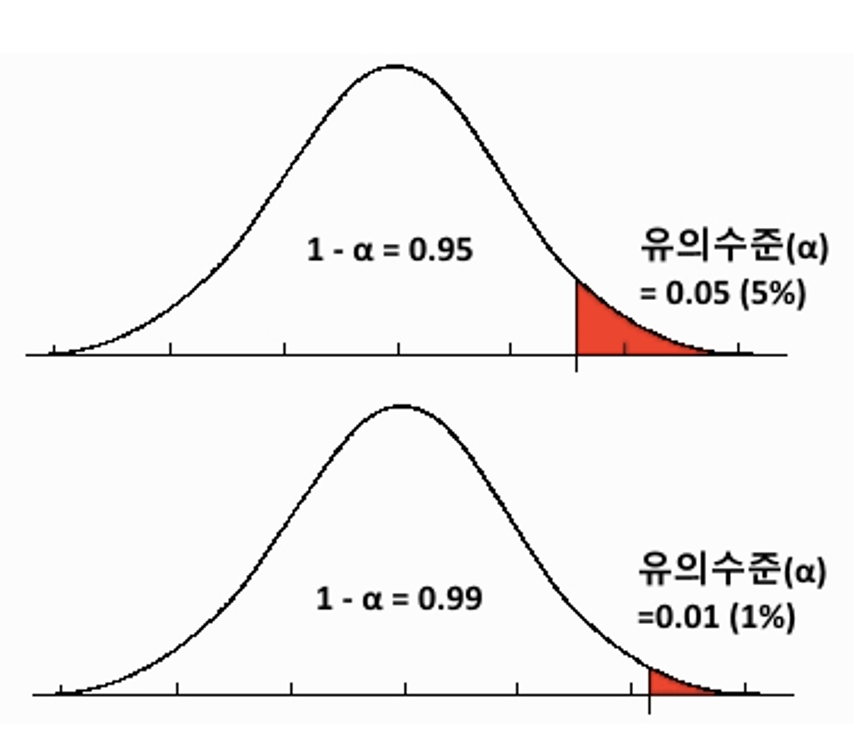
유의수준이란?

귀무가설이 맞을 때 오류허용 기준 (확률)
유의수준은 α로 표시 /
95%의 신뢰도를 기준으로 한다면 (1−0.95)인 0.05값이 유의수준 값이 된다.

유의수준은 신뢰수준의 반대 개념으로 오류가 나타날 확률.

확률값이므로, 0부터 1 사이의 값을 가진다.

유의수준을 0.05로 설정 ? → 95% 신뢰도로 기준을 정한 것 !

가설을 설정하고 유의수준을 정한 다음, 실험을 완료하게 되면
실험 전과 후를 비교하면서 유의미했는지 살펴보는데,
결론적으로 귀무가설을 채택할지, 기각할지 결정해야 한다.

📌 검정통계량

결과 해석 단계 1 : 검정 방식 정하고 검정통계량 계산하기

검정통계량이란?

귀무가설을 채택 또는 기각하기 위해 사용하는 확률변수

확률변수란, 특정 확률로 발생하는 각각의 결과를 수치값으로 표현하는 변수

예)
주사위를 던졌을 때 나오는 숫자를 확률변수 X 라고 가정했을 때,
각 X에 대한 확률 P(X) ?
→ 확률변수 X 는 1, 2, 3, 4, 5, 6 이다. (주사위를 던졌을 때 나올 수 있는 모든 수)
→ 주사위 값이 1 ~ 6 중 어떤 수가 나올지 모르기 때문에 이를 확률 변수라고 한다.
→ 각 X에 대한 확률은 1 / 6

검정통계량은 표본 평균, 비율, 상관 계수 간의 차이 등 다양한 형태를 취할 수 있다.
검정 방식의 선택은 가설과 데이터 종류에 따라 달라지는데,

표본 평균 비교

검정 방식 : Z 검정
검정 통계량 : Z - value
비교 대상 : 표본의 평균 (차이 분석) - 모집단의 분산을 알 수 있을 때
대상 : 연속형 데이터
검정 방식 : T 검정
검정 통계량 : T - value
비교 대상 : 표본의 평균 (차이 분석) - 모집단의 분산을 알 수 없을 때
대상 : 연속형 데이터

표본 분산 비교

검정 방식 : 카이제곱 검정
검정 통계량 : x^2 value
비교 대상 : 표본의 분산 (상관관계 분석)
대상 : 범주형 데이터
검정 방식 : F 검정
검정 통계량 : F - value
비교 대상 : 표본의 분산 (상관관계 분석)
대상 : 범주형 데이터

📌 p-value

결과 해석 단계 2 : p - value 확인하기

p - value 란?

어떤 사건이 우연히 발생할 확률
Probability - value 의 줄임말로 확률 을 뜻함.
확률이므로 p - value 는 0 ~ 1 사이의 값을 가진다.

실험의 목표는 대립가설의 채택이므로, 우연히 일어날 확률 (p - value) 이 작으면 좋다.
즉, 유의수준보다 p - value 가 작은 경우에 대립가설을 채택할 수 있다.

p - value 가 0.05(유의수준) 보다 작다 
= 우연히 일어났을 가능성이 거의 없다
= 인과관계가 있다고 추정
= 대립가설 채택

p - value 가 0.05(유의수준) 보다 크다 
= 우연히 일어났을 가능성이 높다
= 인과관계가 없다고 추정
= 대립가설 기각

중심극한정리를 통해, 모집단이 큰 경우 표본 평균이 정규 분포를 따르게 된다고 가정

📌 실습

# 라이브러리 호출
import pandas as pd
import numpy as np
# 과학 계산용 파이썬 라이브러리 (*)
import scipy.stats as stats
from PIL import Image

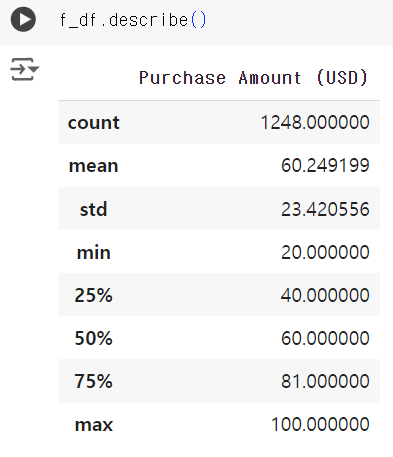
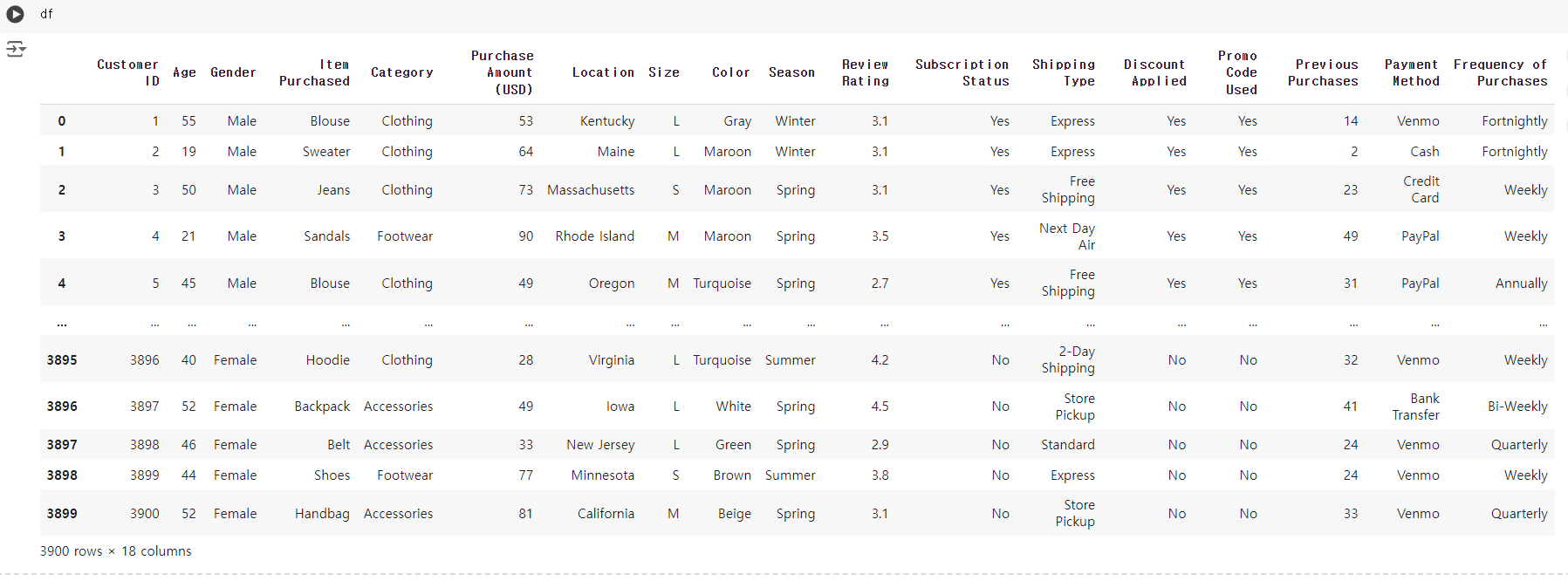
데이터 불러오기 & 확인

T - test

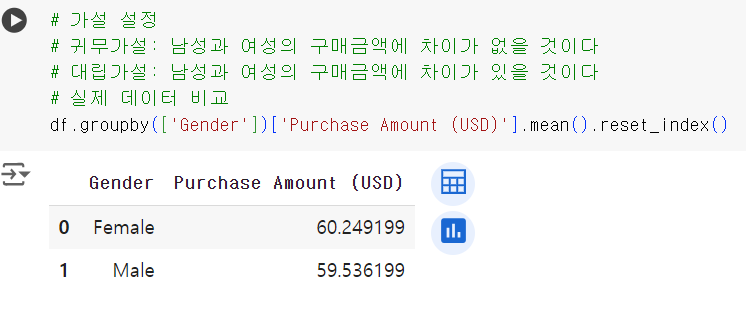
# 가설 설정
# 귀무가설: 남성과 여성의 구매금액에 차이가 없을 것이다
# 대립가설: 남성과 여성의 구매금액에 차이가 있을 것이다
# 데이터 비교
df.groupby(['Gender'])['Purchase Amount (USD)'].mean().reset_index()

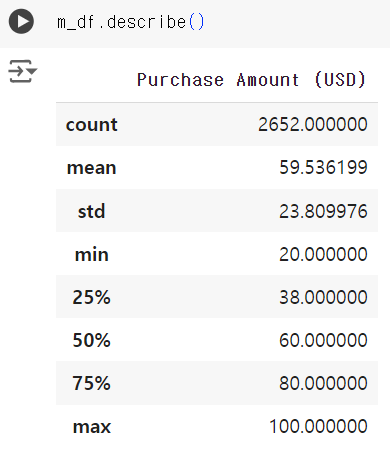
# 데이터 분리
# mask method
mask=(df['Gender']=='Male')
mask1 = (df['Gender']=='Female')
m_df = df[mask]
f_df = df[mask1]

# 결제금액 컬럼만 가져오기
m_df=m_df[['Purchase Amount (USD)']]
f_df=f_df[['Purchase Amount (USD)']]

# 차이가 있는 것으로 보여짐
# 유의수준은 통상적으로 많이 쓰이는 0.05 로 정함
# scipy 라이브러리를 이용해 t - score 와 p - value 를 확인할 수 있다.
# t - test 는 표본의 평균(차이 분석)을 알고자 할 때 사용되며, 모집단의 분산을 알 수 없는 경우 주로 사용
t, pvalue=stats.ttest_ind(m_df, f_df)

# t - score 는 그룹 간 얼마나 차이가 있는지에 대한 지표
# t - score 가 크면 그룹 간 차이가 큼을 의미
# p - value 는 우연에 의해 나타날 확률에 대한 지표
# p - value가 0.05 보다 크다 = 우연히 일어났을 가능성이 높다 = 인과관계가 없다고 추정
# 여기서 p - value 값은 0.05 보다 크므로, 인과관계가 없다고 추정할 수 있다.
# 대립가설 기각
t, pvalue

카이제곱 검정

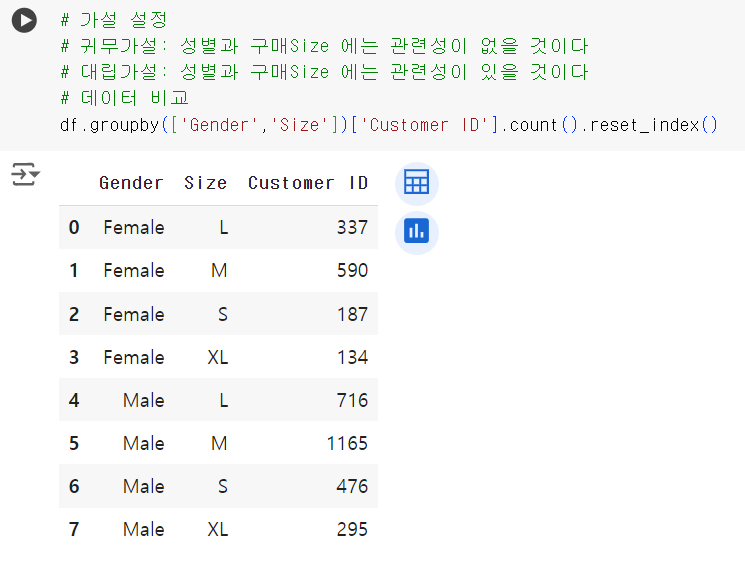
# 가설 설정
# 귀무가설: 성별과 구매Size 에는 관련성이 없을 것이다
# 대립가설: 성별과 구매Size 에는 관련성이 있을 것이다
# 데이터 비교
df.groupby(['Gender','Size'])['Customer ID'].count().reset_index()

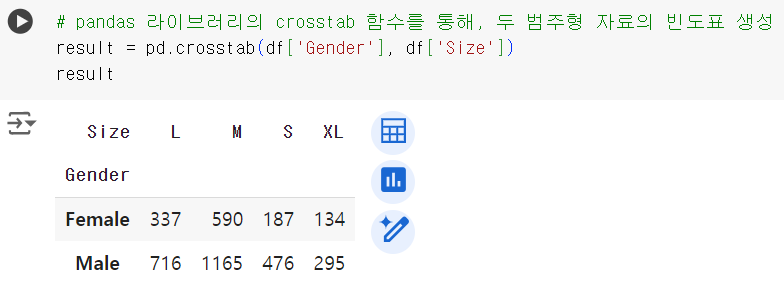
# pandas 라이브러리의 crosstab 함수를 통해, 두 범주형 자료의 빈도표 생성
result = pd.crosstab(df['Gender'], df['Size'])
result

# 카이제곱 검정을 stats 함수를 통해 구현
# chi2_contingency를 통해, 카이제곱 통계량, p - value 출력 가능
stats.chi2_contingency(observed=result)

# 각 값들을 별도로 보기
# 카이제곱 검정 통계량, p - value, 자유도 확인 가능
stats.chi2_contingency(observed=result)[0]

# p - value 는 우연에 의해 나타날 확률에 대한 지표
# p - value가 0.05 보다 크다 = 우연히 일어났을 가능성이 높다 = 인과관계가 없다고 추정
# 여기서 p - value 값은 0.05 보다 크므로, 인과관계가 없다고 추정
# 대립가설 기각
stats.chi2_contingency(observed=result)[1]

# 자유도와 유의수준을 통해 귀무가설 기각 여부를 판단하기도 한다.
# 자유도란, (변수1 그룹의 수 - 1)*(변수2 그룹의 수 - 1)
# 1 * 3 = 3 이 도출
stats.chi2_contingency(observed=result)[2]

codataffee

커피 좋아하는 데이터 꿈나무

이전 포스트

STATISTICS#1

다음 포스트