그래프(Graph)
- 정점과 정점 사이를 연결하는 간선으로 이루어진 비선형 자료구조이다.
- 정점과 간선의 집합으로 표현할 수 있다.
정점 ?
노드(node)라고도 하며 정점에는 데이터가 저장된다.
간선 ?
링크라고도 하며 노드간의 관계를 나타낸다.
특징
- 정점은 여러 개의 간선을 가질 수 있다.
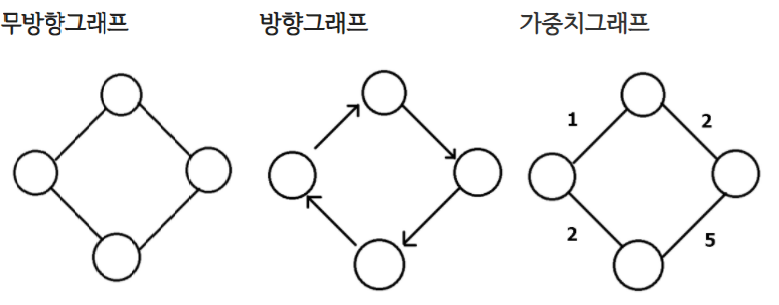
- 크게 방향 그래프와 무방향 그래프로 나눌 수 있다.
- 간선은 가중치를 가질 수 있다.
- 사이클(순환경로를 말하며 경로의 시작 정점과 종료 정점이 동일한 경우)이 발생할 수 있다.
구현방법
그래프를 구현하는 방법에는 인접행렬(Adjacency Materix)과 인접리스트 방식(Adjacency List)이 있다. 두 개의 구현 방식은 각각의 상반된 장단점을 가지고 있으며 대부분 인접리스트 형식을 많이 사용한다.
1. 인접행렬
-
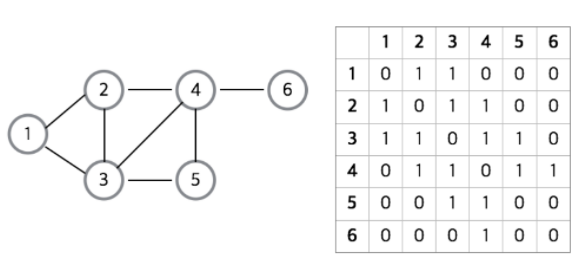
그래프의 노드를 2차원 배열로 만든 것이다.
-
각 정점의 연결정보를 0과 1로 표현한다.
const graph = Array.from(new Array(7), () => new Array(7).fill(0));
graph[1][2] = 1;
graph[1][3] = 1;
graph[2][1] = 1;
graph[2][3] = 1;
graph[2][4] = 1;
graph[3][1] = 1;
graph[3][2] = 1;
graph[3][4] = 1;
graph[3][5] = 1;
graph[4][2] = 1;
graph[4][3] = 1;
graph[4][5] = 1;
graph[4][6] = 1;
graph[5][3] = 1;
graph[5][4] = 1;
graph[6][4] = 1;
for(let i = 1; i < graph.length; i++) {
console.log(graph[i].slice(1).join(' ')); // 0번 정점이 없으므로 제거
}
// 결과
// 0 1 1 0 0 0
// 1 0 1 1 0 0
// 1 1 0 1 1 0
// 0 1 1 0 1 1
// 0 0 1 1 0 0
// 0 0 0 1 0 0
장점
-
2차원 배열 안에 모든 정점들의 간선 정보가 포함되므로 배열의 위치를 확인하면 두 정점의 연결 정보를 탐색할 때 O(1)의 상수 시간복잡도로 가능하다.
-
구현이 비교적 간단하다.
단점
-
모든 정점에 대해 간선 정보를 대입해야 하므로 인접행렬 생성에 O(N^2)의 시간복잡도 소요.
-
무조건 2차원 배열이 필요하므로 메모리의 낭비가 심하다.
2. 인접리스트
-
그래프의 노드들을 연결 리스트로 표현한다.
-
주로 정점의 연결 리스트 배열을 만들어 관계를 설정하여 구현한다.
const graph = Array.from(new Array(7), () => []);
graph[1].push(2);
graph[1].push(3);
graph[2].push(1);
graph[2].push(3);
graph[2].push(4);
graph[3].push(1);
graph[3].push(2);
graph[3].push(4);
graph[3].push(5);
graph[4].push(2);
graph[4].push(3);
graph[4].push(5);
graph[4].push(6);
graph[5].push(3);
graph[5].push(4);
graph[6].push(4);
console.log(graph); // 0번 정점은 없으므로 1 인덱스(정점) 배열부터 ~ 6까지의 연결정보
장점
-
정점들의 연결 정보를 탐색할 때 O(n)의 시간복잡도. (n: 간선의 갯수)
-
필요한 만큼의 공간만 사용하기때문에 공간의 낭비가 적습니다.
단점
-
특정 두 점이 연결되었는지 탐색하려면 인접행렬에 비해 시간이 오래 걸립니다. (배열보다 연결리스트가 탐색속도 느림)
-
구현이 비교적 어렵습니다.
