해시테이블(HashTable)

• 키와 값의 한 쌍을 이루는 데이터를 저장하는 자료구조이다.

• 데이터(키와 값)의 키를 해시 함수에 통과시켜 나온 키를 인덱스(해시)로 사용하여 그 인덱스에 값을 저장한다.

  해시 함수 (hash function) : 임의의 길이를 가지는 키를 고정된 길이의 키로 매핑해주는 함수
  해시 (hash) : 해시 함수의 결과로 반환 되는 값을 가리킨다.

• 빠른 속도로 데이터를 검색할 수 있으며 이는 내부적으로 배열을 사용하기 때문이다.
  
  

해시 함수(Hash Function)

• 임의의 길이를 가지는 키를 고정 길이의 키로 매핑해주는 함수.
• 해시 함수의 결과로 해시를 반환한다.
• 결국 해시 함수는 고유한 해시 값을 설정하는 것이 중요하다.

// 간단한 해시 함수의 구현

function hashFunction(key) {
  return key % 10;
}

console.log(hashFunction(1001)); // 해시 : 1
console.log(hashFunction(1234)); // 해시 : 4

해시의 충돌(Collision)

• 해시 테이블의 대표적인 단점으로, 서로 다른 키를 해시 함수에 넣었지만 동일한 해시값이 나오는것을 해시의 충돌이라 부른다.
• 해시의 충돌의 해결 방법은 대표적으로 개방주소법(Open Address)과 분리연결법(Separate Chaining)으로 나뉘어진다.

function hashFunction(key) {
  return key % 10;
}

// 충돌 발생 !!
console.log(hashFunction(1001)); // 해시 : 1
console.log(hashFunction(11)); // 해시 : 1
console.log(hashFunction(21)); // 해시 : 1
console.log(hashFunction(31)); // 해시 : 1

1. 개방주소법

• 개방주소법은 해시 충돌이 발생하면 테이블 내의 비어있는 공간의 새로운 인덱스를 찾아 해시값을 저장하는 방법이다.
• 개방주소법은 어떠한 방식으로 비어있는 공간을 탐색하는 지에 따라 방법이 여러가지가 존재한다.
  
  

1-1. 선형 탐사법(Linear Probling)

• 선형 형태로 배열을 순차적으로 탐사하는 방법이다.

• 위의 충돌 상황에서 선형 탐사법은 아래와 같이 값이 저장된 이후의 빈 공간을 탐색하여 값을 저장한다.
  
  

• 이러한 선형 탐사법의 단점은 특정 해시 값의 주변에만 모두 채워져 있는 일차 군집화 문제에 취약하다.

• 같은 해시가 여러 번 나오는 상황이라면, 선형 탐사법을 사용하면 데이터가 연속되게 저장될 가능성이 높아집니다. 이런 경우 해시의 값이 1이 나왔을 때뿐만 아니라 2나 3이 나왔을 때도 충돌이 발생합니다. 이미 해시 값으로 2, 3에 해당하는 곳에 데이터가 저장되어있기 때문에, 계속해서 해시 값으로 1이 나왔고, 새롭게 2, 3이 나오더라도, 저장하려고 하는 공간에 데이터가 있기 때문에 충돌이 나게 됩니다.
  
  

1-2. 제곱 탐사법(Quadratic Probing)

• 위와 같은 선형 탐사법의 일차 군집화 문제를 조금이나마 보완한 방법이다.
• 선형 탐사법과의 차이점은 탐사하는 폭이 고정폭이 아닌 제곱으로 늘어나는 부분이 차이가 있다.
• 첫 번째 충돌이 발생했을 때는 충돌 난 지점을부터 1의 제곱만큼, 두 번째 충돌이 발생했을 때는 2의 제곱만큼, 세 번째는 3의 제곱만큼 탐사하는 구간의 폭이 빠르게 커집니다. 선형 탐사법 때와 동일한 상황에서 제곱 탐사법을 사용하면 해시 테이블은 아래와 같은 모양이 됩니다.

• 이렇게 제곱 탐사법을 사용하면 충돌이 발생하더라도 데이터의 밀집도가 선형 탐사법보다 많이 낮기 때문에 다른 해시값까지 영향을 받아서 연쇄적으로 충돌이 발생할 확률이 많이 줄어듭니다.

• 하지만 여전히 해시로 1이 여러 번 나오면 계속 충돌이 발생하고, 결국 데이터의 이차 군집화가(Secondary Clustering) 발생합니다.
  
  

1-3. 이중해싱(Double Hashing)

• 위의 방법들을 보완하고자 나온 방법이다.
• 해시함수를 이중으로 사용한다.
• 기존과 마찬가지로 하나의 해시함수는 최초 해시를 얻을 때 사용하고, 다른 하나는 충돌이 났을 경우 탐사 이동폭을 얻기 위해 사용한다.
• 이렇게 하면 위의 방법들보다 다른 공간에 값이 골고루 저장될 확률이 높아진다.

'use strict';

// 개방주소법 : 이중 해싱을 적용한 해시 테이블 구현

// 테이블 사이즈가 소수여야 효과가 좋다
// 스텝 해시에 사용되는 수는 테이블 사이즈보다 약간 작은 소수를 사용한다.

// 테이블사이즈와 두 번째 해시함수 둘 중에 하나가 소수가 아니라면 결국 언젠가 같은 해싱이 반복되기 때문이다.

class HashTable {
  constructor(size) {
    this.table = new Array(size); // 해시테이블의 크기
    this.size = 0; // 해시테이블에 채워진 데이터 크기
  }

  getFirstHash(key) {
    return Number(key) % this.table.length;
  }

  getSecondHash(key) {
    return this.table.length - 6 - (key % (this.table.length - 6));
  }

  setValue(data) {
    let idx = this.getFirstHash(Object.keys(data)[0]);

    while (true) {
      if (!this.table[idx]) {
        this.table[idx] = data;
        console.log(`${idx}번 인덱스에 ${Object.values(data)[0]} 저장 !`);
        this.size++;
        return;
      } else if (this.size >= this.table.length) {
        console.log('해시테이블이 가득 찼습니다.');
        return;
      } else {
        console.log(
          `${idx}번 인덱스에 ${Object.values(data)[0]} 저장하려다 충돌 발생 !`
        );
        idx += this.getSecondHash(Object.keys(data));
        idx = idx > this.table.size ? idx - this.table.length : idx;
      }
    }
  }

  getValue(key) {
    let idx = this.getFirstHash(key);

    if (!this.table[idx]) {
      console.log('존재하지 않는 데이터입니다.');
      return;
    }

    while (true) {
      if (Object.keys(this.table[idx]).includes(String(key))) {
        console.log(Object.values(this.table[idx])[0]);
        return;
      } else {
        idx += this.getSecondHash(key);
        idx = idx > this.table.size ? idx - this.table.length : idx;
      }
    }
  }
}

const hashTable = new HashTable(23);

hashTable.setValue({ 1991: 1 });
hashTable.setValue({ 6: 2 });
hashTable.setValue({ 13: 3 });
hashTable.setValue({ 21: 4 });

hashTable.getValue(1991);
hashTable.getValue(6);
hashTable.getValue(13);
hashTable.getValue(21);

console.log(hashTable);

• 결과
  
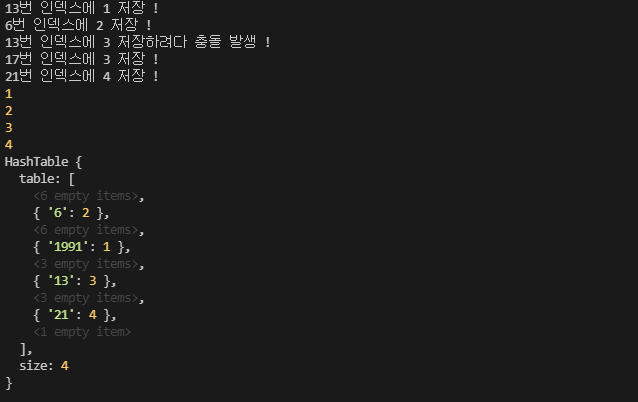
• 선형 탐사법과 제곱 탐사법을 사용했다면 모두 해시의 결과가 1이어서 연쇄적으로 충돌이 발생해야 할 값들이지만 이중 해싱을 사용함으로써 한번의 충돌만으로 모든 값을 저장할 수 있게 되었다. 테이블이 꽉 차면 결국 풀방입니다가 출력된다.
  
  
  

2. 분리 연결법

• 분리 연결법은 개방 주소법과는 다른 개념으로 접근하는 충돌 우회 방법이다.
• 분리 연결법은 해시테이블의 공간에 하나의 값이 아니라 링크트 리스트나 트리를 사용한다.

'use strict';

// 분리 연결법 : 해시 테이블의 충돌을 연결 리스트로 해결하는 방법으로 구현

class Node {
  constructor(key, value) {
    this.key = key;
    this.value = value;
    this.next = null;
  }
}

class LinkedList {
  constructor() {
    this.head = null;
    this.tail = null;
    this.length = 0;
  }

  add(key, value) {
    const newNode = new Node(key, value);

    if (this.empty()) {
      this.head = newNode;
      this.tail = newNode;
    } else {
      this.tail.next = newNode;
      this.tail = newNode;
    }

    this.length++;
  }

  remove(key) {
    if (this.empty()) {
      console.log('해시테이블에 데이터가 존재하지 않습니다.');
      return;
    }

    let curNode = this.head;
    let prevNode = this.head;

    while (curNode) {
      if (curNode.key === key) {
        if (this.length === 1) {
          this.head = null;
          this.tail = null;

          console.log(`삭제한 데이터 값 : ${curNode.value}`);
        } else {
          if (curNode === this.head) {
            this.head = curNode.next;
          } else if (curNode !== this.head && curNode !== this.tail) {
            prevNode.next = curNode.next;
          } else {
            this.tail = prevNode;
            this.tail.next = null;
          }

          console.log(`삭제한 데이터 값 : ${curNode.value}`);
        }

        this.length--;

        return;
      }

      prevNode = curNode;
      curNode = curNode.next;
    }

    console.log('삭제하려는 데이터가 존재하지 않습니다.');

    return;
  }

  search(key) {
    let curNode = this.head;

    while (curNode) {
      if (curNode.key === key) {
        console.log(`조회한 데이터 값 : ${curNode.value}`);
        return;
      }

      curNode = curNode.next;
    }

    // 키값이 조회가 안되는 경우
    console.log('존재하지 않는 데이터 입니다.');
    return;
  }

  empty() {
    return this.length === 0 ? true : false;
  }
}

class HashTable {
  constructor() {
    this.table = new Array(23); // 해시테이블의 크기
    this.size = 0; // 해시테이블에 채워진 데이터 크기
  }

  getHash(key) {
    return key.length % this.table.length;
  }

  setValue(key, value) {
    const idx = this.getHash(key);

    if (!this.table[idx]) {
      const linkedList = new LinkedList();
      linkedList.add(key, value);
      this.table[idx] = linkedList;
    } else {
      this.table[idx].add(key, value);
    }

    this.size++;
  }

  getValue(key) {
    const idx = this.getHash(key);

    this.table[idx].search(key);

    return;
  }

  removeValue(key) {
    const idx = this.getHash(key);

    this.table[idx].remove(key);

    if (!this.table[idx].head) {
      delete this.table[idx];
    }

    return;
  }
}

const hashTable = new HashTable(23);

hashTable.setValue('mike', '010-1234-5678');
hashTable.setValue('smith', '010-1111-2222');
hashTable.setValue('sam', '010-4444-5555');
hashTable.setValue('sola', '010-6666-7777');

console.log(hashTable.table);

hashTable.getValue('mike');
hashTable.getValue('smith');
hashTable.getValue('sam');
hashTable.getValue('sola');
hashTable.getValue('soll');

// 하나씩 삭제해보며 결과값을 확인 해보자.
hashTable.removeValue('mike');
hashTable.removeValue('smith');
hashTable.removeValue('sam');
hashTable.removeValue('sola');

console.log(hashTable.table);

• 결과
  

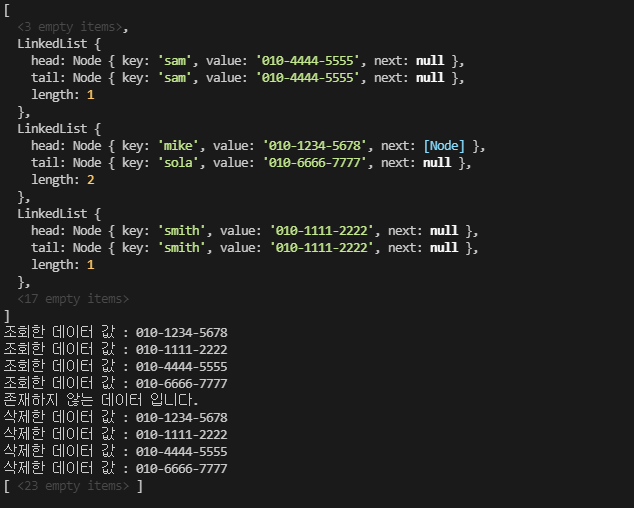
정리

• 해시 테이블은 고정적인 공간을 할당해서 많은 데이터를 담기 위한 자료구조인 만큼 언젠가 데이터가 테이블의 공간을 가득 채우게 된다.

• 개방 주소법을 사용한 경우 테이블의 공간이 가득 차게 될 것 이며, 분리 연결법을 사용한 경우는 테이블에 빈 공간도 적어지고 충돌이 발생하는 경우가 많아지게 된다면 리스트의 길이가 너무 길어지게되어 리스트의 탐색시간이 길어질 것 이다.

• 위와 같은 이유로 해시테이블은 공간을 가득 채우기보다는 어느 정도 비워져 있는 상황에서의 성능이 더 좋다.

• 해시테이블 사용 시 어느정도 테이블의 공간이 적어지면 테이블의 크기를 재할당 해야한다.
  
  
  
  

참고자료

• https://evan-moon.github.io/2019/06/25/hashtable-with-js/
• https://mingcoder.me/2019/12/25/Programming/Algorithm/hash-table-implement/