그래프2 : (최소신장트리, 프림알고리즘, 크루스칼알고리즘, 최단경로, 다익스트라 알고리즘, 벨만-포드 알고리즘, 플로이드-워샬 알고리즘)

📚 1. 최소신장트리

💡 신장트리(spanning tree)

• 그래프의 간선을 '정점 수 - 1' 만큼 남겨 만든 트리
• ex) 너비우선트리, 깊이우선트리
  💡 최소 신장트리(spanning tree)
• 간선들의 가중치 합이 가장 작게 되도록 만든 신장트리
• ex) 여러 가구에 전력을 공급하기 위한 공급망의 설계

📚 2. 프림알고리즘

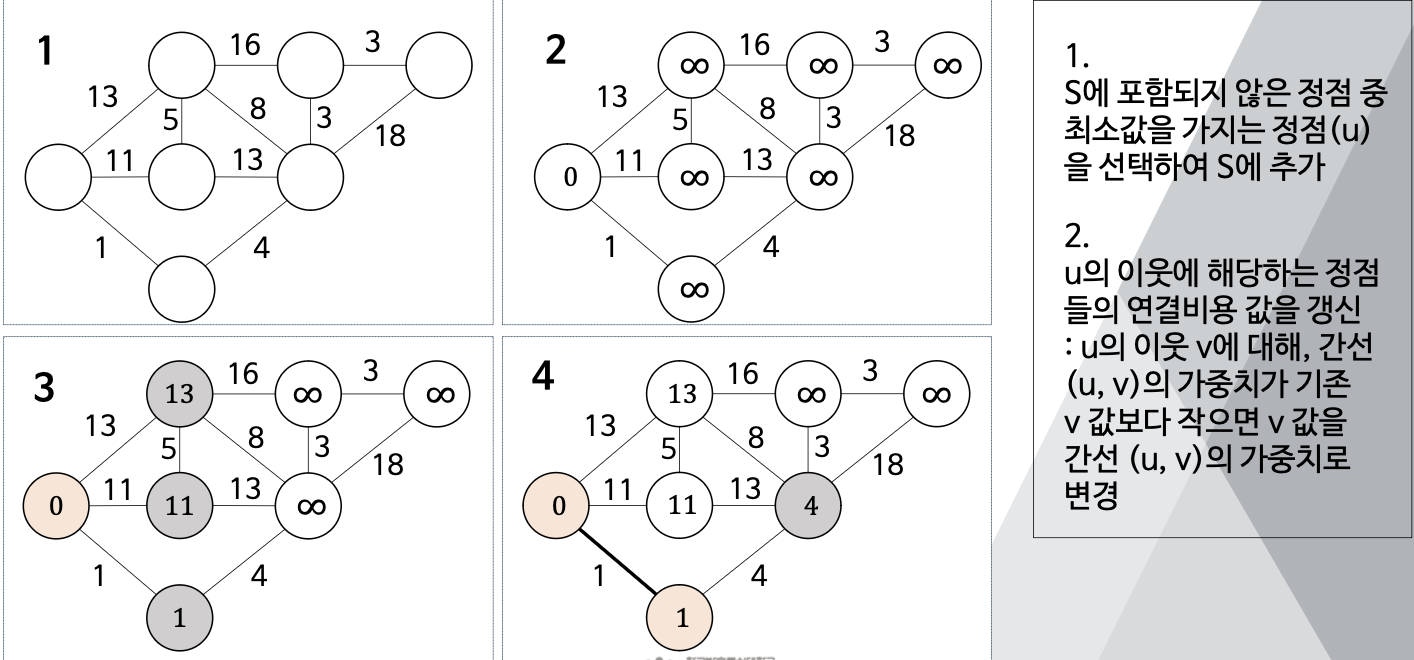
💡 프림알고리즘

• 1. 최소신장트리에 포함된 정점으로 이루어진 집합 S생성
• 2. 시작 정점을 제외한 모든 정점에 연결비용 값을 무한대로 설정(시작 정점은 0으로)
• 3. 모든 정점이 집합 S에 포함될 때까지 반복
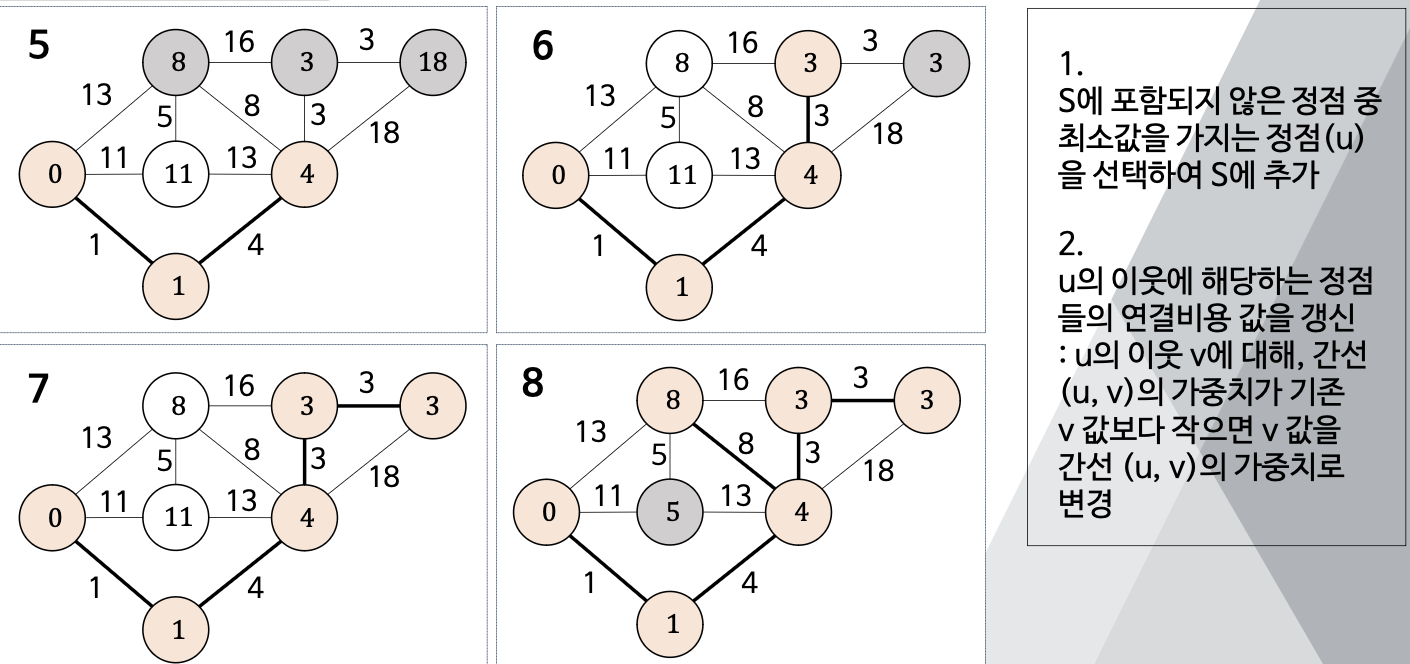
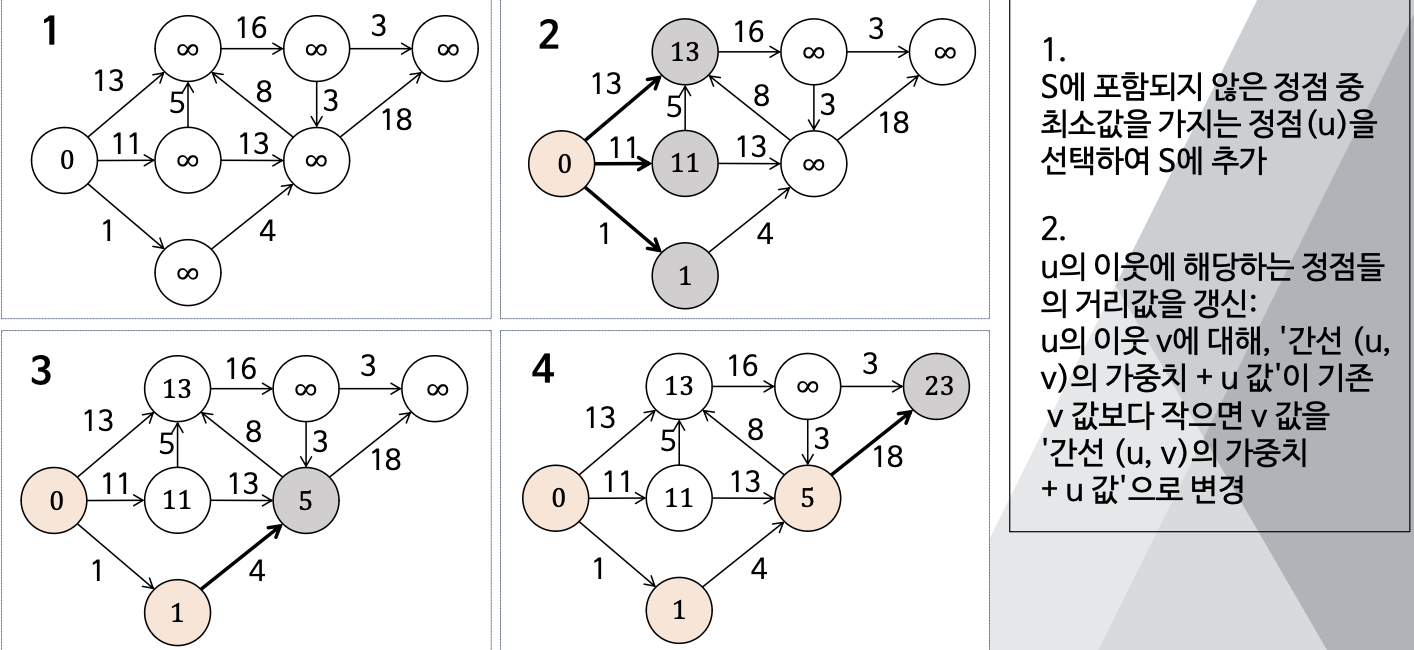
     (1) S에 포함되지 않은 정점 중 최소값을 가지는 정점(u)를 선택하여 S에 추가
     (2) u의 이웃에 해당하는 정점들의 연결비용 값을 갱신 : u의 이웃 v에 대해, 간선 (u,v)의 가중치가 기존 v값보다 작으면 v값을 간선(u,v)의 가중치로 변경
     

💡 프림알고리즘의 시간복잡도

• 모든 정점이 S에 포함될 때까지 반복 -> V
  • S에 포함되지 않은 정점 중 최소값을 가지는 정점(u)를 선택하여 S에 추가 -> logV(힙정렬을 사용할 경우 최소값 제거 후 수선 비용)
  • u의 이웃에 해당하는 정점들의 연결비용 값을 갱신
    • E x, u의 이웃 v에 대해, 간선 (u,v)의 가중치가 기존 v값보다 작으면 v값을 간선 (u,v)의 가중치로 변경
    • logV (힙에서 원소값이 변했을 때 수선에 필요한 비용)
• 시간 복잡도: O(VlogV + ElovV) -> O(ElogV)

💡 프림알고리즘의 구현

def primMST(self):

	key = [sys.maxint] * self.V
	parent = [None] * self.V
   
	key[0] = 0
   
	mstSet = [False] * self.V
   
	parent[0] = -1
   
	for cout in range(self.V):
		u = self.minKey(key, mstSet)
		mstSet[u] = True
       
		for v in range(self.V):
       
			if self.graph[u][v] > 0 and mstSet[v] == False and \
			key[v] > self.graph[u][v]:
           
				key[v] = self.graph[u][v]
				parent[v] = u

📚 3. 크루스칼 알고리즘

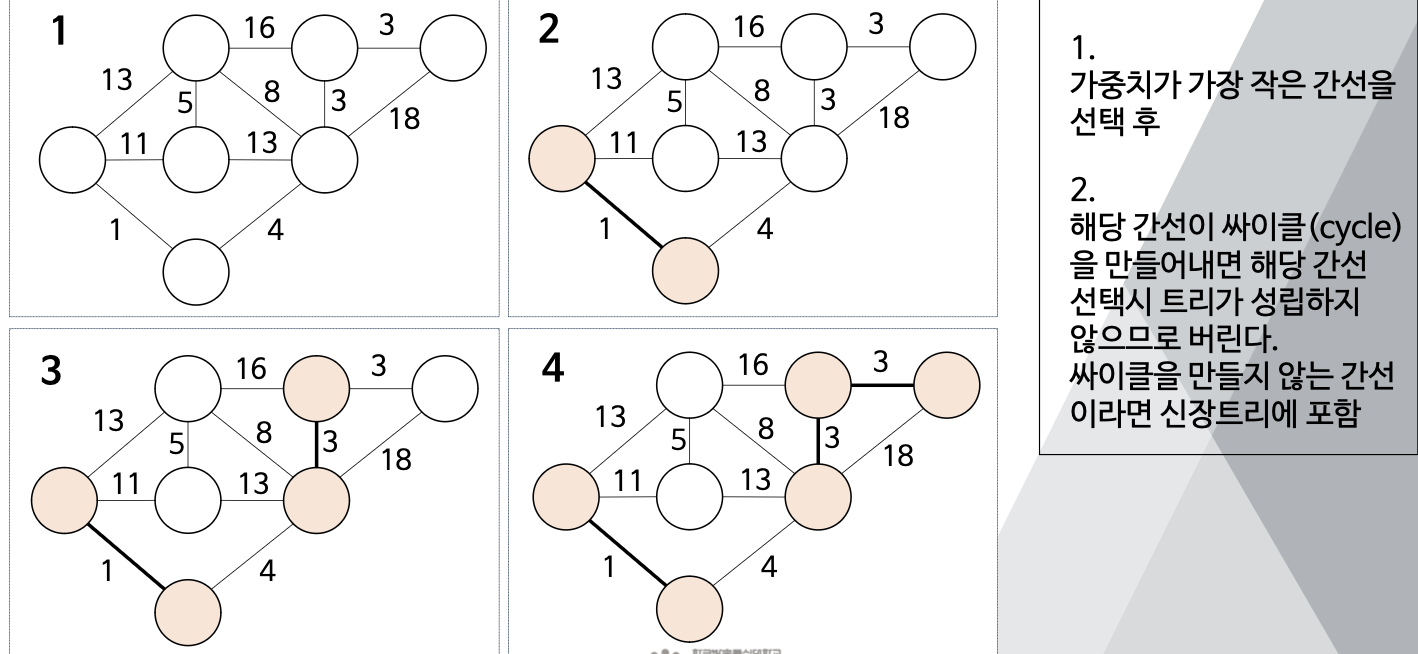
💡 크루스칼 알고리즘

• 간선들을 가중치의 크기 순으로 정렬
• 신장트리에 포함된 간선의 수가 '정점 수 - 1'이 될 때까지 반복
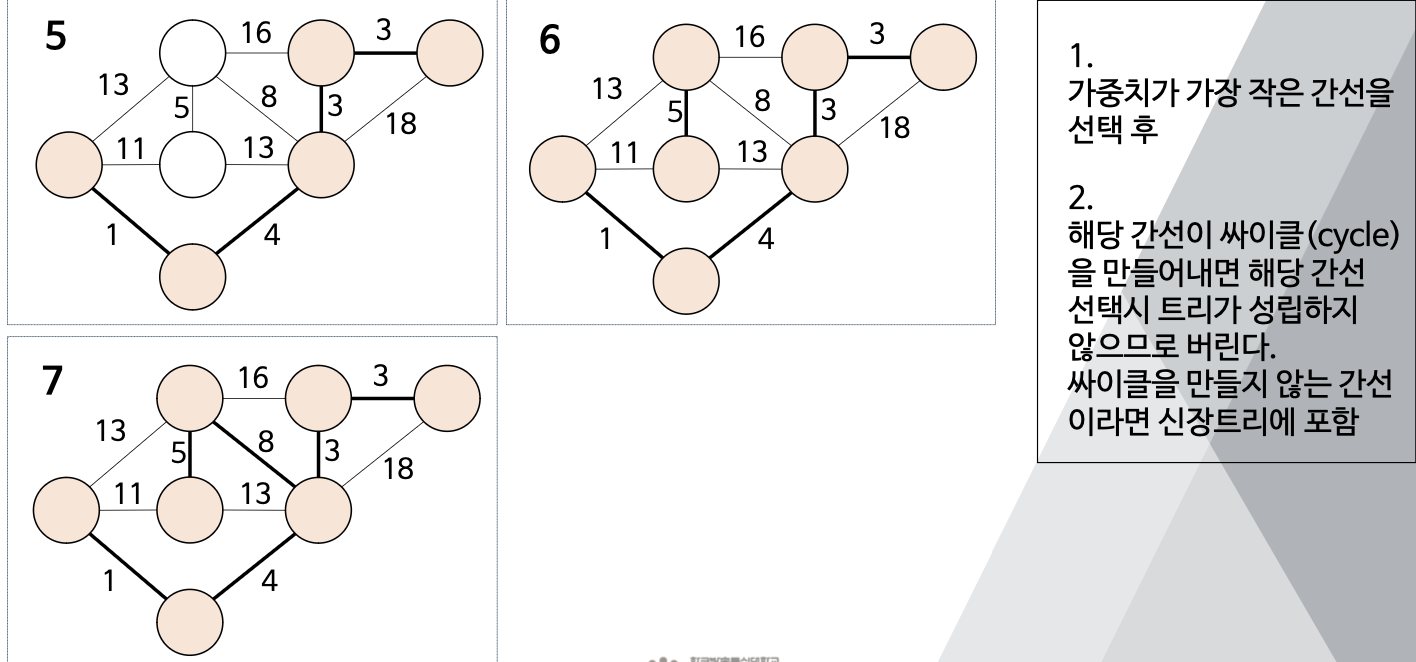
  (1) : 가중치가 가장 작은 간선 선택.
  (2) : 해당 간선이 싸이클을 만들어내면 해당 간석 선택시 트리가 성립하지 않으므로 버리고, 만들지 않는 간선이라면 신장트리에 포함.
  

💡 크루스칼 알고리즘의 시간복잡도

• 간선들을 가중치의 크기 순으로 정렬 -> O(ElogE)
• 신장트리에 포함된 간선의 수가 '정점 수 -1'이 될 때까지 반복함
  • (1) : 가중치가 가장 작은 간선을 선택 후
  • (2) : 해당 간선이 싸이클을 만들어내면 해당 간선 선택시 트리가 성립하지 않으므로 버림, 싸이클을 만들어 내지 않는 간선이라면 신장트리에 포함
• 시간 복잡도: O(ElogE) -> O(ElogV)

💡 크루스칼 알고리즘의 구현

def KruskalMST(self):
...
	# Step 1: Sort all the edges in non-decreasing order of their weight.
	self.graph = sorted(self.graph, key=lambda item: item[2])
	
    # Number of edges to be taken is equal to V-1
	while e < self.V - 1:
		# Step 2: Pick the smallest edge
		u, v, w = self.graph[i]
		...
		# If including this edge does't cause cycle, include it in result
		# and increment the index of result for next edge

		if not is_cycle(u, v, result, self.graph):
			e = e + 1
			result.append([u, v, w])
		# Else discard the edge

📚 4. 최단 경로

💡 최단경로 문제

• 경로의 길이 : 경로가 포함하는 간선들의 가중치 합
• 그래프의 시작 정점에서 도착 정점까지의 최단경로를 찾는 문제
• 네비게이션, 물류, 공장의 부품 이동 최적화 등의 문제에 적용

📚 5. 다익스트라 알고리즘

💡 다익스트라 알고리즘

• 시작 정점으로부터 모든 다른 정즘으로의 최단경로를 구하는 알고리즘
• 음의 가중치가 없는 경우에만 성립
• 프림알고리즘과 유사
  • 프림 알고리즘은 각 정점의 값이 신장트리에 연결하는 최소비용을 나타내기 위해 사용되지만 다익스트라 알고리즘은 최단거리를 판단하기 위해 사용

💡 다익스트라 알고리즘 동작 방식

• 1. 최단경로의 계산이 끝난 정저들의 집합 S를 생성
• 2. 시작 정점을 제외한 모든 정점의 거리 값을 무한대로 저장 (시작 정점은 0으로)
• 3. 모든 정점이 집합 S에 포함될 때까지 반복
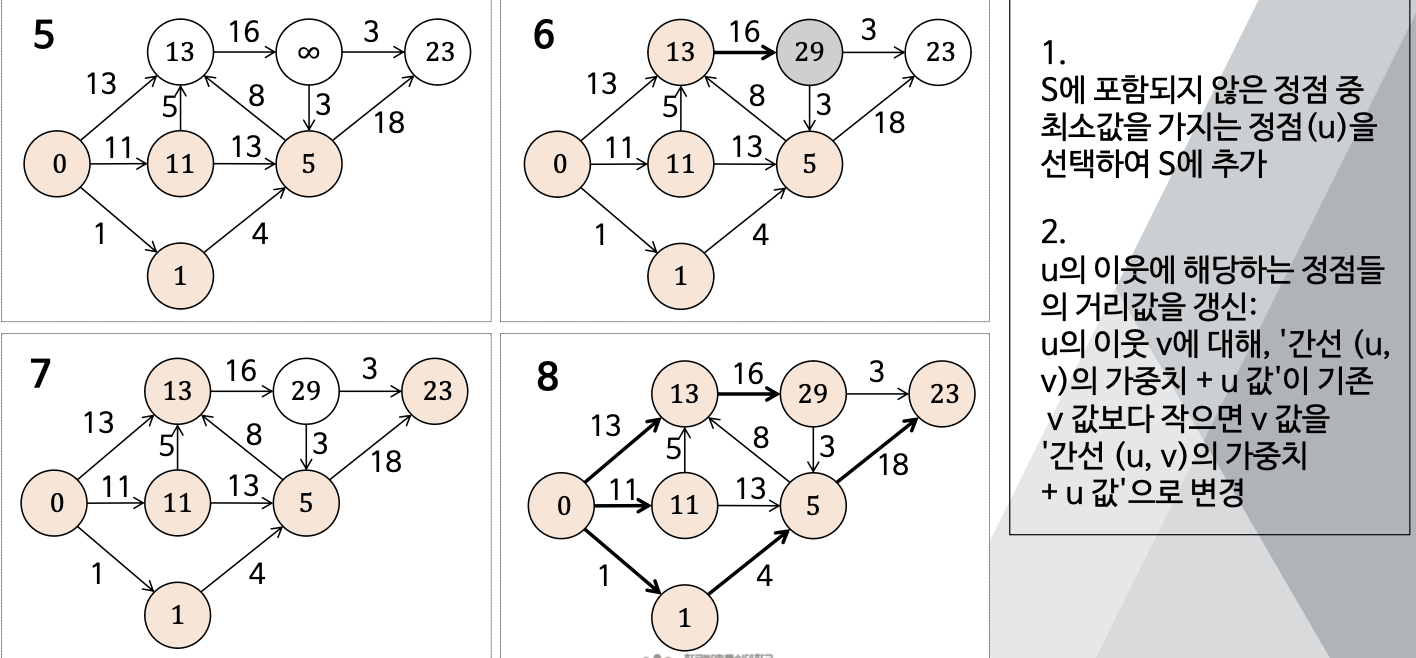
     (1). S에 포함되지 않은 정점 중 최소값을 가지는 정점(u)을 선택하여 S에 추가
     (2). u의 이웃에 해당하는 정점들의 거리값을 갱신: u의 이웃 v에 대해, '간선 (u, v)의 가중치 + u 값'이 기존 v 값보다 작으면 v 값을'간선 (u, v)의 가중치 + u 값'으로 변경
     

💡 다익스트라 알고리즘의 시간복잡도

• 프림알고리즘과 구조가 완전히 같으므로 O(ElogV)

💡 다익스트라 알고리즘의 구현

def dijkstra(self, src):

	dist = [sys.maxint] * self.V
	dist[src] = 0
   
	sptSet = [False] * self.V
   
	for cout in range(self.V):
		x = self.minDistance(dist, sptSet)
		sptSet[x] = True
       
	# Update dist value of the adjacent vertices
	# of the picked vertex only if the current
	# distance is greater than new distance and
	# the vertex in not in the shortest path tree
   
	for y in range(self.V):
   
		if self.graph[x][y] > 0 and sptSet[y] == False and \
		dist[y] > dist[x] + self.graph[x][y]:
			dist[y] = dist[x] + self.graph[x][y]

📚 6. 벨만-포드 알고리즘

💡 벨만-포드 알고리즘

• 시작 정즘으로부터 모든 다른 정점으로의 최단경로를 구하는 알고리즘
• 음의 가중치가 존재하는 경우에도 성립 (음의 싸이클은 허용되지 않음)

💡 벨만-포드 알고리즘 동작 방식

• 1. 시작 정점을 제외한 모든 정점의 거리 값을 무한대로 저장 (시작 정점은 0으로)
• 2. 다음 단계를'정점 수(|𝑉|) - 1'만큼 반복
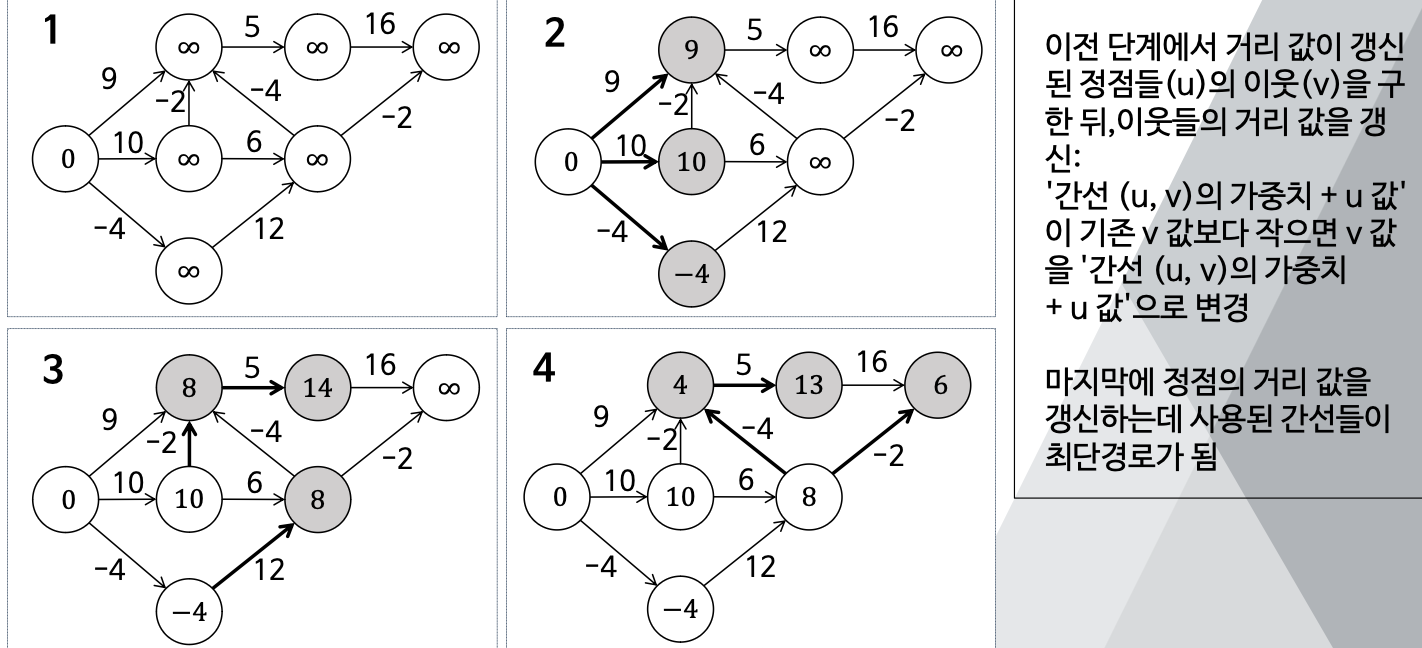
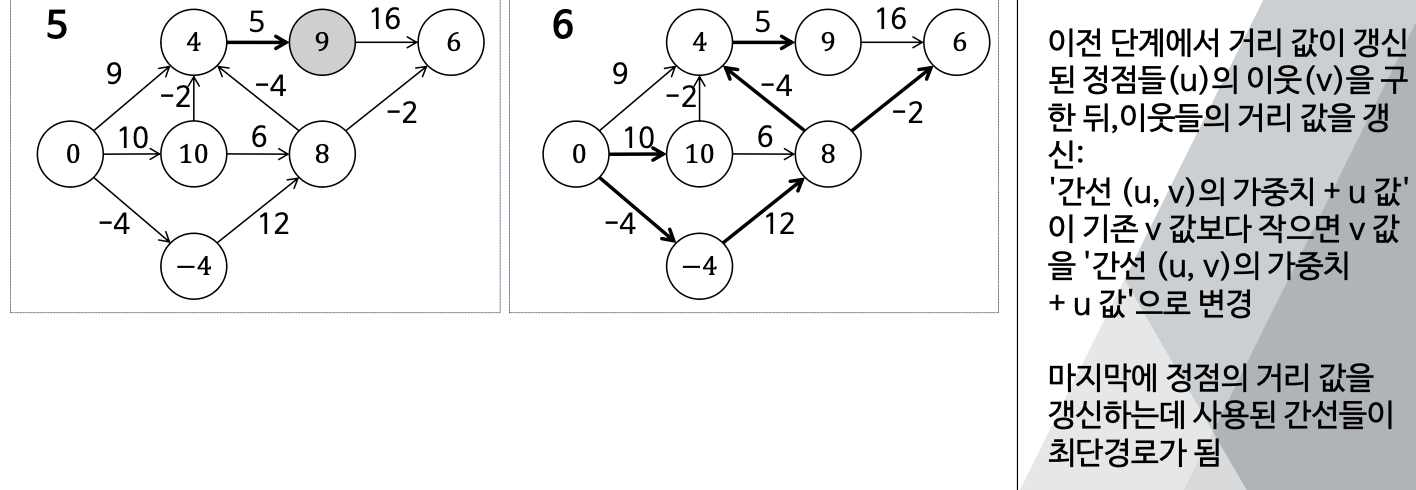
     * (1) 이전 단계에서 거리 값이 갱신된 정점들(u)의 이웃(v)을 구한 뒤, 이웃들의 거리 값을 갱신:
     '간선 (u, v)의 가중치 + u 값'이 기존 v 값보다 작으면 v 값을 '간선 (u, v)의 가중치 + u 값'으로 변경
• 3. 마지막에 정점의 거리 값을 갱신하는데 사용된 간선들이 최단경로가 됨
     

💡 벨만-포드 알고리즘의 시간복잡도

• 시작 정점을 제외한 모든 정점의 거리 값을 무한대로 저장 (시작 정점은 0으로) -> 상수 시간
• 다음 단계를 정줌수(|V|) - 1만큼 반복 -> V X
  * 이전 단계에서 거리 값이 갱신된 정점들(u)의 이웃(v)을 구한 뒤,이웃들의 거리 값을 갱신: → 𝐸 ×
  '간선 (u, v)의 가중치 + u 값'이 기존 v 값보다 작으면 v 값을'간선 (u, v)의 가중치 + u 값'으로 변경 → 상수 시간
• 시간복잡도 : O(VE)

💡 벨만-포드 알고리즘의 구현

def BellmanFord(self, src):
	# Step 1: Initialize distances from src to all other vertices as INFINITE
   
	dist = [float("Inf")] * self.V
	dist[src] = 0

	# Step 2: Relax all edges |V| - 1 times. A simple shortest
	# path from src to any other vertex can have at-most |V| - 1 edges
	
    for _ in range(self.V - 1):
		# Update dist value and parent index of the adjacent vertices of
		# the picked vertex. Consider only those vertices which are still in queue
       
		for u, v, w in self.graph:
       
			if dist[u] != float("Inf") and dist[u] + w < dist[v]: 
            	dist[v] = dist[u] + w

📚 7. 플로이드-워샬 알고리즘

💡 플로이드-워샬 알고리즘

• 모든 정점 쌍 사이의 최단경로를 구하는 알고리즘

💡 플로이드-워샬 알고리즘 구현

for i in vertices:
	for j in vertices:
		dist[i][j] = weight[i][j]

for k in vertices:
	for i in vertices:
		for j in vertices:
			if dist[i][k] + dist[k][j] < dist[i][j]:
				dist[i][j] = dist[i][k] + dist[k][j]

💡 플로이드-워샬 알고리즘의 시간복잡도

• 플로이드-워샬 알고리즘의 시간복잡도 : O(V^3)