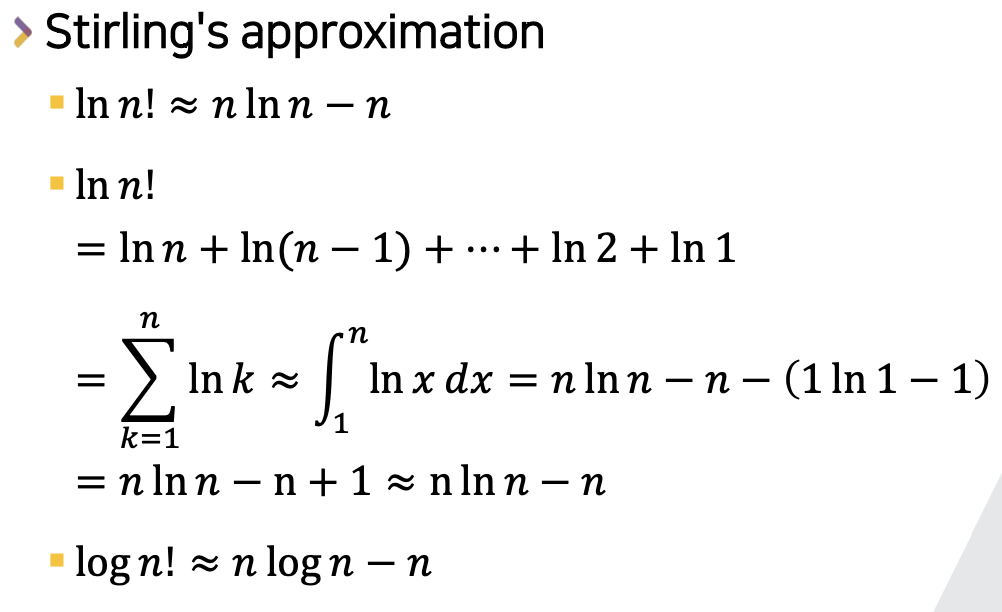정렬3: (팀정렬, 정렬 시간의 하한, 계수정렬, 기수정렬)

📚 1. 팀정렬

💡 팀정렬이란?

• Python의 정렬 알고리즘으로 구현됨.
• 아이디어: 삽입정렬과 병합연산 (병합정렬에서 두 배열을 합치는데 사용됨)을 결합.
• 점근적인 시간복잡도는 O(nlogn)으로 병합정렬 힙정렬과 동일하지만 평균적인 성능에는 차이가 있음.

💡 팀정렬의 과정?

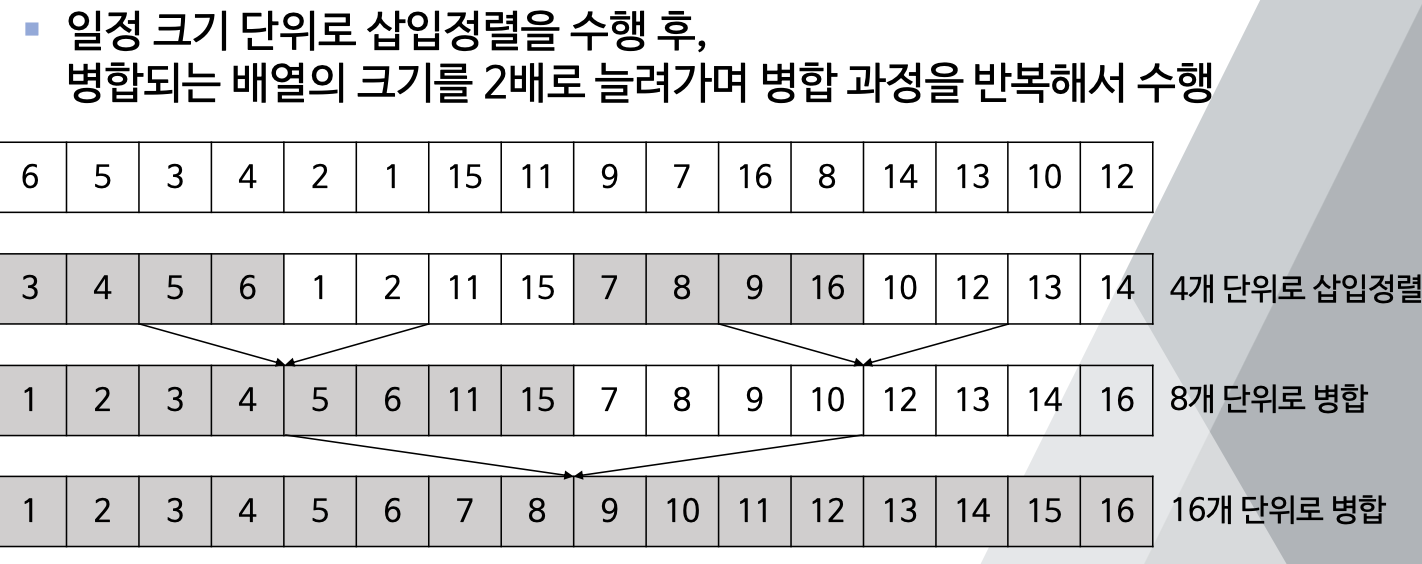
• 일정 크기 단위로 삽입 정렬을 수행 후, 병합되는 배열의 크기를 2배로 늘려가며 병합 과정을 반복해서 수행.
  

💡 팀정렬의 구현

💡 팀정렬의 시간 복잡도?

• 삽입정렬을 수행하는 단계
  • size 단위로 삽입정렬을 n / size 횟수만큼 수행
  • 삽입정렬의 시간복잡도는 O(n^2 (# n = size))이므로 size^2 (n / size) = size n
  • O(size * n)에서 size는 상수이므로 이 단계에서는 O(n)이 소요됨.
• 병합을 수행하는 단계
  • 병합 횟수 t (# size * 2^t = n => O(logn))
  • 1회 병합에 소요되는 시간 : n
  • 병합 단계에 소요되는 총 시간 : O(nlogn)
• 삽입정렬 단계에서는 O(n), 병합 단계에서는 O(nlogn)이 소요되므로 팀정렬의 최종적인 시간복잡도는 O(nlogn).

📚 2. 정렬 시간의 하한

💡 정렬 시간의 하한 이란?

• O(nlogn)보다 빠른 정렬 알고리즘이 존재할 수도 있지 않을까?

💡 결정트리

• 주어진 데이터들을 분류하기 위한 트리 구조
  • 내부 노드 : 분류 조건
  • 리프 노드 : label

💡 정렬 : 결정트리 탐색

• 비교정렬(두 원소의 비교를 통한 정렬)을 결정트리의 어느 리프 노드에 해당하는지 탐색하는 과정으로 볼 수 있음.
  
• 이 경우 정렬에 소요되는 시간은 루트에서 리프까지 도달하는데 거친 간선의 수에 비례.
• 최악의 경우 소요되는 시간은 트리의 높이와 비례함.

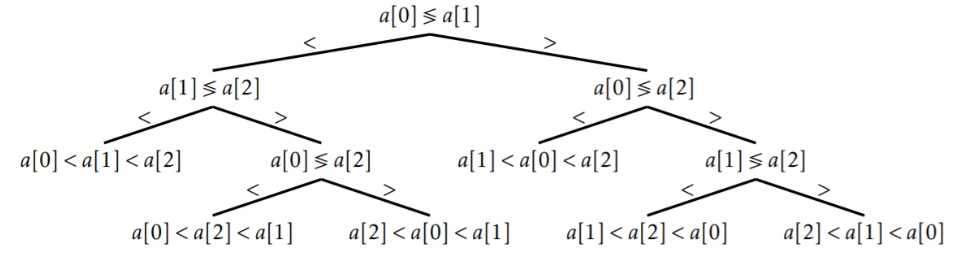
💡 정렬에 필요한 비교 횟수

• 위 그림에서 n개의 원소를 정렬했을 때 나올 수 있는 가능성은 n!개가 존재
• 위 그림에서 n개 원소의 정렬은 n!개의 리프 노드를 가진 결정트리의 탐색, 최악의 소요시간은 n!개의 리프 노드를 가진 이진트리의 높이에 비례

💡 n!개의 리프노드를 가진 이진트리의 높이

• n!개의 리프노드를 가진 이진트리의 높이는 최소 log2n!
  • 이진트리의 경우 레벨이 하나 내려갈 때마다 이전보다 최대 2배씩 노드 수가 많아 질 수 있으므로 2^height = n!
• 비교정렬의 시간복잡도 하한: O(log(n!))

💡스털링의 근사식

• ln(n!)이 nlnn - n으로 근사 될수 있음을 나타내는 식
• => log(n!)이 nlogn - n으로 근사 할 수 있음.
• 따라서 O(log(n!)) -> O(nlogn)
  • 정리 : 비교정렬은 결정트리로 나타낼 수 있고, 최악의 경우, 트리의 높이는 log(n!)과 비례했었고 이는 스털링의 근사식을 사용하면, nlogn으로 근사가 되므로 하한을 nlogn으로 설정하게 됨.

📚 3. 계수정렬 (비교 정렬에 속하지 않는 특수한 정렬)

💡 계수정렬 (counting sort) 이란?

• 정렬하고자 하는 원소들이 k개의 연속된 정수값 중에 하나로만 이루어져 있을 때 O(n) 시간에 정렬을 끝낼 수 있는 방법.(k >> n)일때
• 원소들이 특정 범위의 연속된 정수값을 가지기 때문에 어떤 원소가 몇 개씩 있는지를 안다면 정렬되었을 때 각 원소들을 어디에 배치해야 할지 계산할 수 있음.

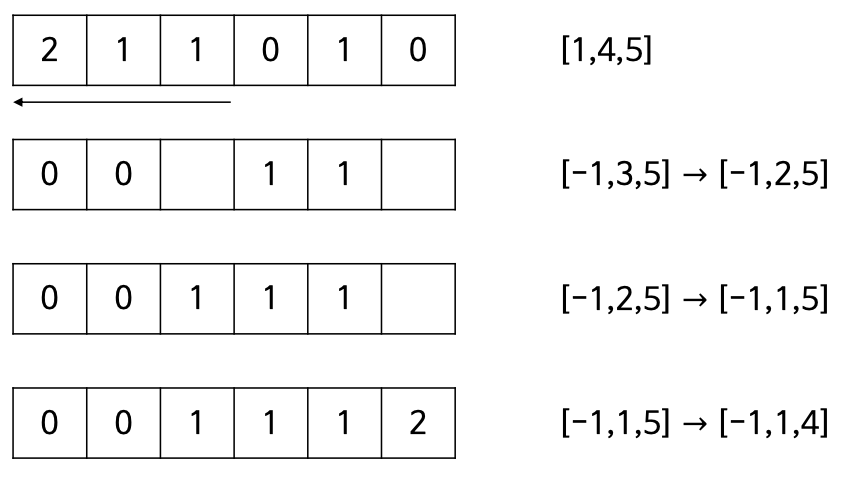
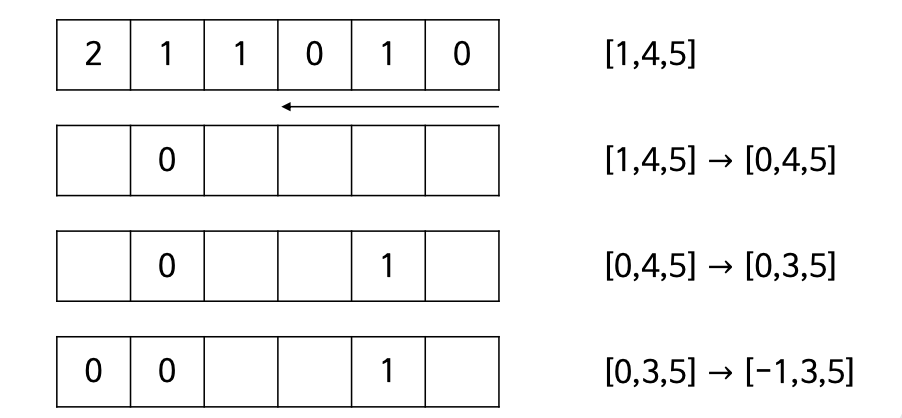
💡 계수정렬의 과정?

• 1. 원소값별로 원소의 개수를 셈.
• 2. 각 원소들이 위치해야 하는 마지막 인덱스를 원소값별로 계산
• 3. 배열의 마지막 원소부터 앞으로 순회하며 새로운 배열에 원소를 하나씩 배치하고 해당 원소값의 인덱스를 1씩 감소.

💡 계수정렬의 구현

counting_sort(a,k)
	# 원소가 0부터 k-1 까지의 값을 가지는 경우
	c ← new_zero_array(k) # 원소값별 개수를 저장할 크기 k의 배열

    for i in 0,1,2,...,length(a) − 1 do
    	c[a[i]] ← c[a[i]] + 1 # 원소를 종류별로 카운트
       
	for i in 1,2,3,...,k − 1 do
		c[i] ← c[i] + c[i − 1] # 원소의 개수를 마지막 인덱스로 변환
       
	b ← new_array(length(a)) # 원소들을 위치시킬 배열 생성

	# 배열 a를 순환하며 만나는 원소를 계산해 놓은 인덱스(c[a[i]])에 따라 b에 저장
	for i in length(a) − 1,length(a) − 2,length(a) − 3,...,0 do
		c[a[i]] ← c[a[i]] − 1 # 원소가 b에 저장될 때마다 해당 인덱스 1 감소
		b[c[a[i]]] ← a[i]
       
	return b

💡 계수정렬의 시간 복잡도?

• 첫번째 루프에서 O(n)시간 두번째 루프에서 O(k)시간, 세번째 루프에서 O(n)시간이 소요되므로 O(n + k)시간
  • k << n 일 경우 시간복잡도 : O(n)

💡 계수정렬의 안전성?

• 정렬시의 안정성 : 값이 같은 원소인 경우에 두 원소의 원래 순서를 그래도 유지하면서 정렬하는 성질
  

📚 4. 기수정렬 (비교 정렬에 속하지 않는 특수한 정렬)

💡 기수정렬 이란?

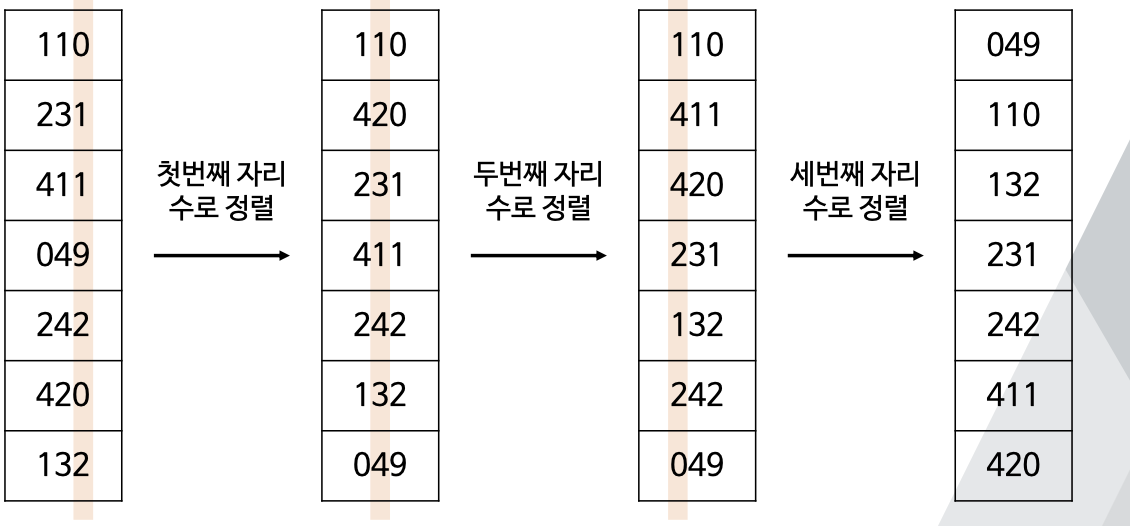
• 정렬하고자 하는 원소가 k자리 이하의 자연수인 경우 사용
  

• 위 그림과 같이 세 자리 이하인 경우, 매 자리 수로 차례대로 정렬

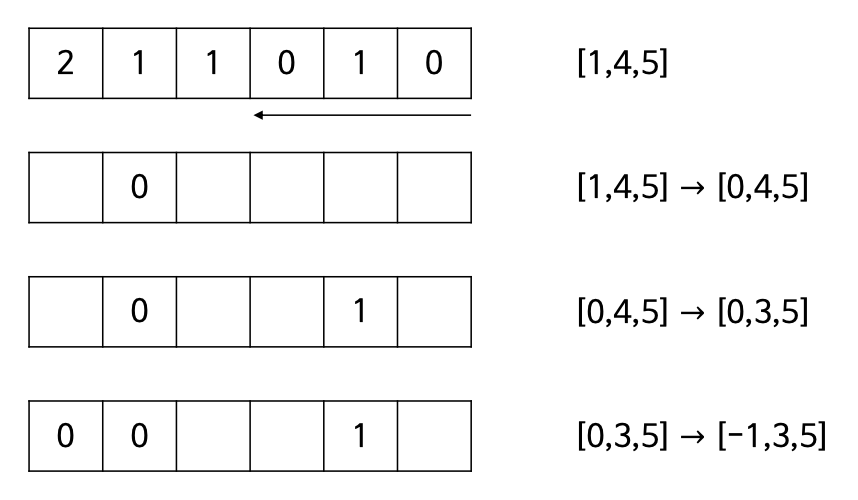
💡 기수정렬의 과정

• 1. 가장 아래 자리부터 자리수 기준으로 정렬
• 2. 정렬이 완료되면 하나 위 자리로 이동해서 해당 자리수 기준으로 정렬하는 작업 방법
• 3. 맨 위 자리까지 정렬이 완료되면 완료.

• 각자리를 정렬할 때 계수정렬과 같이.
  • 안정적으로 정렬을 수행하는 방법을 사용 : 현재 자리수 기준으로 정렬할 때 다른 자리수에서 졍렬해 놓은 순서를 바꾸게 되면 곤란.
  • O(n) 시간에 끝나는 정렬 알고리즘을 사용. : 한 자리수 기준으로 정렬하므로 정렬하는 원소의 값이 0 ~ 9 사이의 정수값만을 가짐.

💡 기수정렬의 시간 복잡도?

• 각 자리를 정렬하는데 계수정렬을 사용하면 O(n) 시간이 소요되는데, k개의 자리에 대해 정렬을 수행하므로 O(kn)이 되지만 k는 상수이므로 총 소요되는 시간복잡도 = O(n)