📚 1. 이진검색트리
💡 이진검색트리 도입 배경
- 어떤 데이터의 순서가 정렬된 정렬배열에서는 시간복잡도가 O(n)만큼 소요됐었고, 이를 보안하기 위해 도입됨.
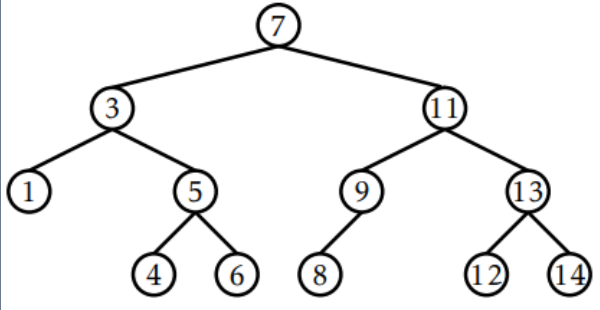
💡 이진검색트리란
- 트리의 모든 노드u에 대해 u의 값이 u.left를 루트로 하는 서브트리의 모든 노드 값보다 크고, u.right를 루트로 하는 서브트리의 모든 노드 값보다 작은 이진트리.
📚 2. 이진검색트리 구현 (추가, 탐색)
💡 이진검색트리 에서 추가와 탐색
find_eq(x) w <- r while w != nil do if x < w.x then w <- w.left else if x > w.x w <- w.right else return w.x return nil find(x) # x가 없을 경우 x보다 큰 값중 가장 작은 값을 리턴 w ← r z ← nil while w != nil do if x < w.x then z ← w w ← w.left else if x > w.x w ← w.right else return w.x if z = nil then return nil return z.x add(x) # 삽입 p ← find_last(x) return add_child(p,new_node(x)) add_child(p,u) if p = nil then r ← u # 빈 트리를 루트 노드에 저장 else if u.x < p.x then p.left ← u else if u.x > p.x p.right ← u else return false # u.x 이미 트리내에 존재할 때 u.parent ← p n ← n + 1 return true find_last(x) w ← r prev ← nil while w != nil do prev ← w if (x < w.x) then w ← w.left else if (x > w.x) w ← w.right else return w return prev
📚 3. 이진검색트리 구현 (삭제)
💡 이진검색트리 에서 삭제
- u (삭제할 노드) 가 리프일 경우 : u를 삭제
- u가 자식을 하나 가지는 경우 : u를 삭제하고 u의 부모가 u의 자식을 입양
- u가 자식을 두 명 가지는 경우 : u의 자리를 대체할 수 있는 후계자를 찾아서 대체
- u.right를 루트로 하는 서브트리 중 가장 작은 값
remove_node(u) # u가 리프노드이거나 자식을 하나만 가지는 경우 if u.left = nil or u.right = nil then splice(u) # u를 삭제 # u의 자식이 둘인 경우 else w ← u.right # u.right를 서브트리의 루트로 # u.right를 루트로 하는 서브트리 중 가장 작은 값 w를 찾아서 while w.left != nil do w ← w.left u.x ← w.x # u를 w로 대체한 후 splice(w) # w를 삭제 splice(u) if u.left != nil then # u.left가 있으면 s ← u.left # u의 부모에게 u.left를 입양시키기 위해 s에 저장 else # u.left가 없으면 s ← u.right # u.right를 u의 부모에게 입양시키기 위해 s에 저장 if u = r then # u가 루트인 경우에는 r ← s # 입양시킬 자손을 루트로 지정하고 p ← nil # parent는 없음 else # u가 루트가 아니라면 p ← u.parent # u.parent를 p에 저장하고 if p.left = u then # u가 부모의 왼쪽에 있었던 노드라면 p.left ← s # 입양시킬 자손을 부모의 왼쪽으로 입양 else # u가 부모의 오른쪽에 있었던 노드라면 p.right ← s # 입양시킬 자손을 부모의 오른쪽으로 입양 if s != nil then # 입양시킬 자손이 없었던 경우가 아니라면 s.parent ← p # u의 부모를 s의 부모로 지정 n ← n − 1 # 전체 노드 수 1 감소
📚 4. 이진검색트리의 시간복잡도
💡 이진검색트리에서 노드의 검색, 삽입, 삭제는 모두 특정 노드의 탐색이 필요함.
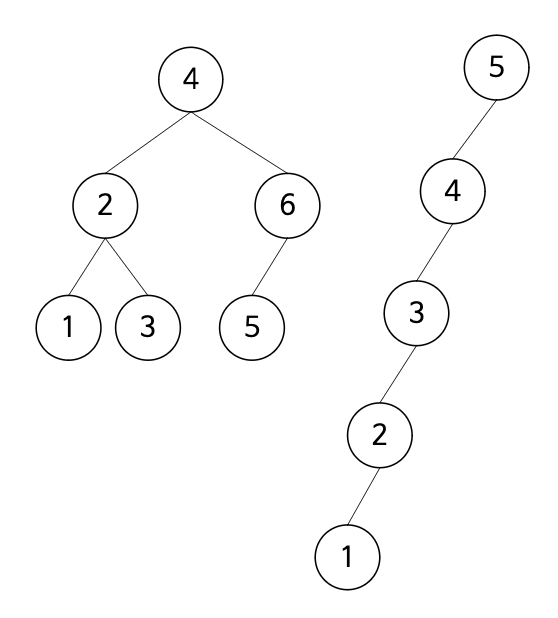
💡 (왼쪽 트리) 균형 잡힌 트리 (좌/우 서브트리의 높이가 비슷한 경우) 에서의 시간복잡도
- 시간과 높이는 비례한다 => O(log(n))
💡 (오른쪽 트리) 불균형 트리 (좌/우 서브트리의 높이가 차이가 큰 경우) 에서의 시간복잡도
- 트리의 불균형이 심한 최악의 경우 => O(n)
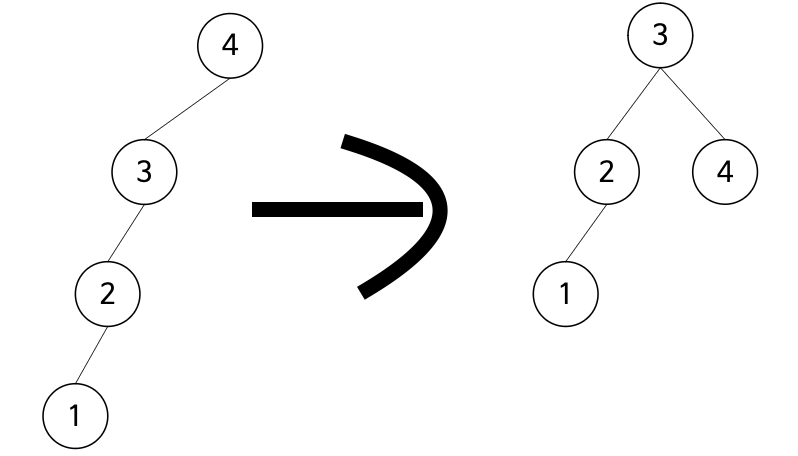
📚 5. 리밸런싱
💡 불균형 트리의 균형이 잡히도록 재조정하는 작업.
- ex) AVL트리, 레드블랙트리