우선순위_큐와_힙

📚 1. 힙의 개념

💡 우선순위 큐 이란?

• 큐와 비슷하지만 원소들이 우선순위를 가지고 있음.
  • 큐는 먼저 들어온 원소가 먼저 처리되는 FIFO구조.
  • 우선순위 큐는 나중에 들어온 원소라도 우선순위가 높을 경우 먼저 처리됨.
• 힙은 우선순위 큐를 구현하는데 사용됨.

💡 힙 이란?

• 이진(binary)힙 : 이진 트리의 한 종류.

• 힙의 조건
  • 1. 부모 노드의 값이 자식 노드보다 작아야 함 -> 루트 노드가 가장 작은 값을 가짐.
  • 2. 트리가 완전해야함 -> 마지막 노드 오른쪽을 제외하고는 모두 채워져야 함.

• 힙의 종류
  • 최소힙
    • 부모의 값이 자식보다 작은 힙
    • 루트에 힙의 최소값이 존재
  • 최대힙
    • 부모의 값이 자식보다 큰 힙
    • 루트에 힙의 최대값이 존재

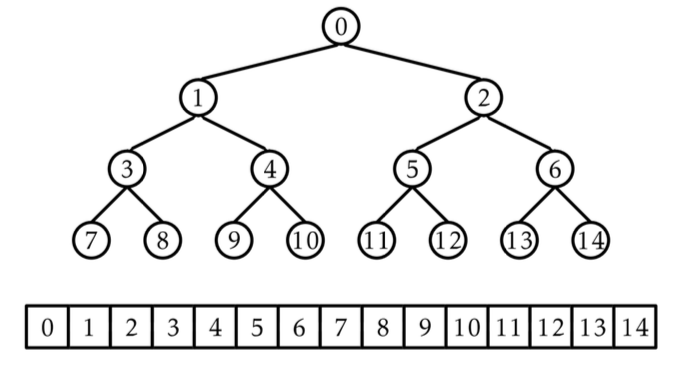
• 배열로 힙을 구현할 때의 인덱스
  

• left child = index * 2 + 1
• right child = index * 2 + 2
• parent = (index - 1) / 2 # 소수점 아래 버림.

📚 2. 힙에서의 삽입

💡 힙에서의 삽입

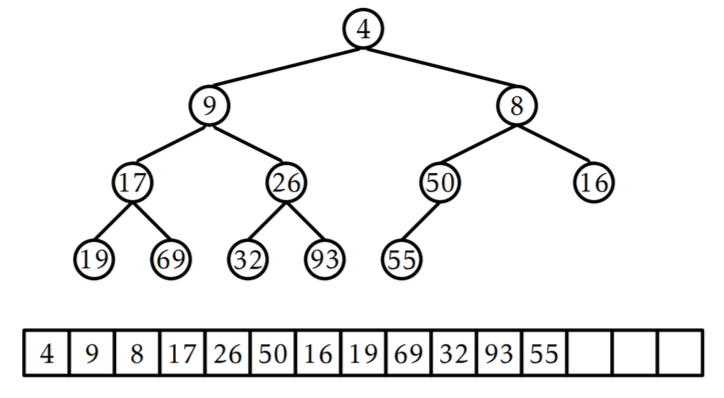
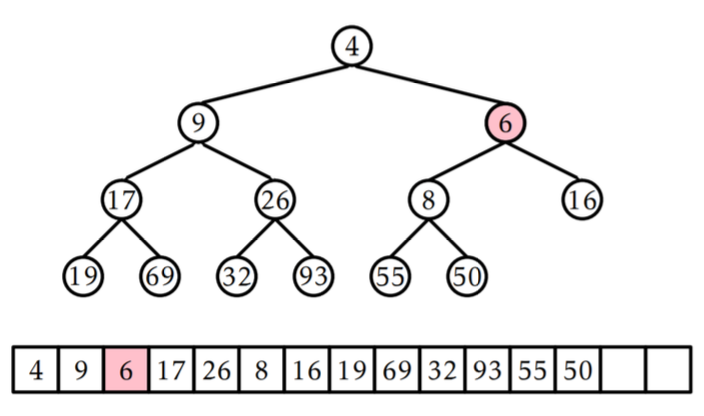
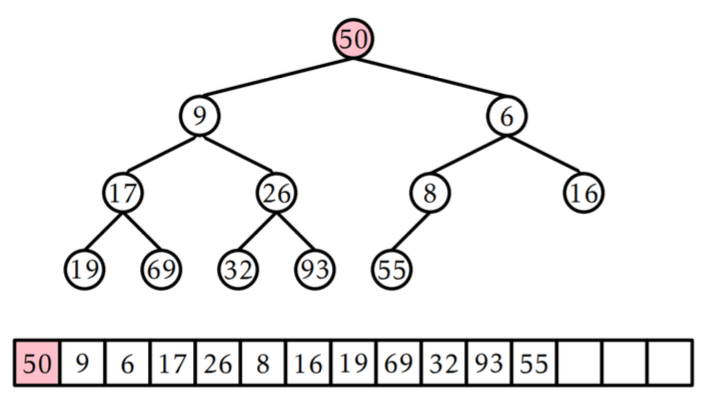
• 위 그림에서 index 6을 추가하고 싶을 때.
  
• 다음과 같이 부모와 자식 노드의 재정의가 필요함.

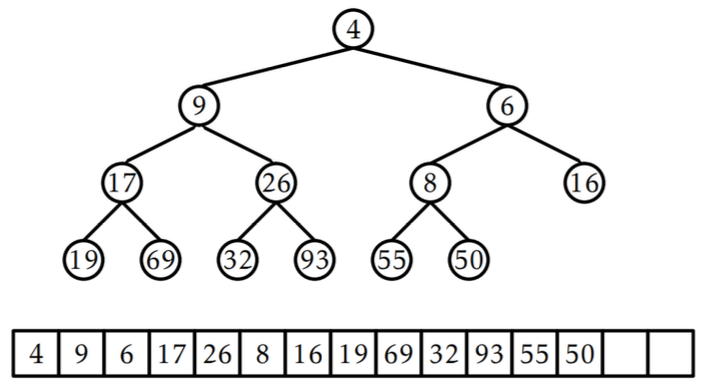
💡 힙에서의 삽입 알고리즘

• 1. 삽입할 값을 노드로 만들어 마지막 노드(트리의 최하단 레벨의 가장 오른쪽 값)의 오른쪽에 추가.
• 2. 추가한 노드의 값과 부모의 값을 비교
• 3. 부모의 값이 노드값보다 크다면, 노드와 부모 노드의 위치를 교환.
• 4. 3번 단계를 더 이상 부모 노드의 값이 크지 않을 때까지 반복.

📚 3. 힙에서의 삽입 구현

💡 힙에서의 삽입 구현

add(X)
	if length(a) < n + 1 then
    	resize()
       
	a[n] <- x # x를 마지막 노드 옆에 추가
    n <- n + 1
    bubble_up(n - 1) # 부모와 비교하며 필요시 위치를 교환
   
    return true


bubble_up(i)
	p <- parent(i) # 주어진 인덱스 i의 부모 인덱스를 계산
   
    while i > 0 and a[i] < a[p] do 
    # i가 루트의 인덱스가 아니고, 부모가 주어진 노드보다 크다는 조건이 성립하는 한,
   
    	a[i],a[p] <- a[p],a[i] # 부모와 값을 서로 교환
        i <- p # 부모의 인덱스에 i 저장
        p <- parent(i) # i의 부모를 다시 p에 저장하고 루프 계속

📚 4. 힙에서의 삭제

💡 힙에서의 삭제

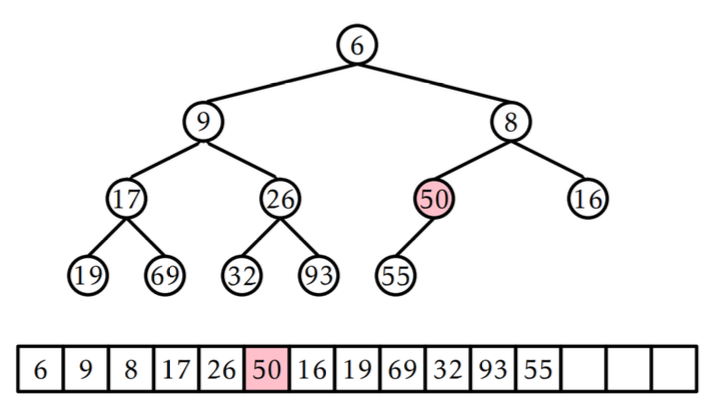
• 우선순위 큐를 바탕으로 고려하면 4가 가장 먼저 삭제가 되게 됨.
  
• 이 경우, 큐에서 가장 오른쪽에 있는 원소가 루트로 오게 됨.
  
• 힙에 조건이 맞을 때까지 부모 자식 위치 재조정.

💡 힙에서의 삭제 알고리즘

• 1. 마지막 노드 (트리의 최하단 레벨의 가장 오른쪽 값) L을 루트의 위치로 옮김.
• 2. L의 자식 중 L보다 작은 값을 가진 자식이 있다면 L과 자식의 위치를 교환.
  • 자식 중 하나만 L보다 작은 값을 가진 경우 -> 해당 자식과 L의 위치를 교환
  • 두 자식 모두 L보다 작은 값을 가진 경우 -> 둘 중 더 작은 값을 가진 자식 노드를 L과 교환
• 3. L의 자식 중 L보다 더 작은 값으 가진 자식이 없을 때까지 2단계를 반복

📚 5. 힙에서의 삭제 구현

💡 힙에서의 삭제 구현

remove()

	x ← a[0] # 루트 노드의 값을 리턴해야 하므로 x에 저장
	a[0] ← a[n − 1] # 마지막 노드를 루트로 이동    
	n ← n − 1
   
	trickle_down(0) # 루트를 자식과 비교하여 필요시 위치를 교환
   
	if 3 · n < length(a) then
		resize()
	return x
  

trickle_down(i)

	while i ≥ 0 do
   
	j ← −1
	r ← right(i) # i 노드의 오른쪽 자식을 r에 저장
   
	if r < n and a[r] < a[i] then # 오른쪽 자식이 i 노드보다 작으면
		l ← left(i) # i의 왼쪽 자식을 l에 저장
       
		if a[l] < a[r] then # 왼쪽 자식이 오른쪽 자식보다 작으면
			j ← l # 교환할 노드로 왼쪽 자식을 저장
		else
			j ← r # 오른쪽 자식이 왼쪽 자식보다 작으면 교환할 노드로 오른쪽 자식을 저장
           
	else # 오른쪽 자식이 i 노드보다 작지 않다면, 왼쪽 자식만이 검토 대상이 되므로
		l ← left(i) # 왼쪽 자식을 l에 저장하고
       
		if l < n and a[l] < a[i] then # 왼쪽 자식이 i 노드보다 작다면
			j ← l # 교환할 노드로 왼쪽 자식을 저장
           
	if j ≥ 0 then # 위의 과정을 거쳐서 바꿔치기할 자식이 존재하면
		a[j],a[i] ← a[i],a[j] # 해당 자식과 i 노드를 교환
       
	i ← j # 교환된 위치인 j를 i에 저장하고 루프 계속    

📚 6. 힙의 성능

💡 삽입과 삭제 연산의 시간 복잡도

• 삽입시에 필요한 bubble_up이나 trickle_down모두 연산 수가 트리의 높이에 비례
  • n개의 노드를 가진 완전 이진트리의 경우 => height = O(logn)
• 힙이 삽입과 삭제 모두 O(logn)이 소요됨. => 힙의 제약조건들이 장점으로 작용

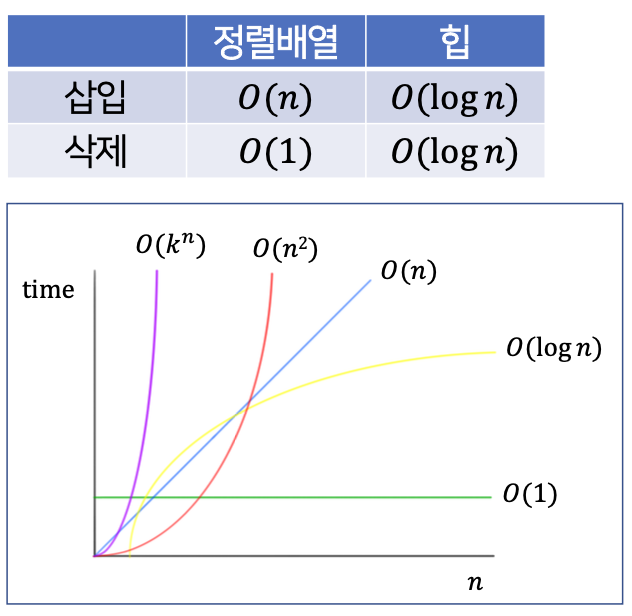
💡 졍렬배열을 이용한 우선순위 큐

• 정렬배열을 우선순위 큐로 사용하는 경우
  • 삽입에는 O(n)이 소요.
  • 삭제의 경우에는 맨 끝의 원소 하나만 삭제와 동시에 리턴하기에 O(1)소요.

💡 힙과 졍렬배열의 비교