재귀 호출

📚 1. 재귀 호출이란

💡 재귀 호출 또는 재귀(recursion)

• 함수 정의 내에서 함수 자신을 호출하는 경우
• 루프를 구현하기 위해 사용
• 어떤 문제를 풀기 위해 풀어야 하는 부분 문제(subproblem)가 원래 문제와 같은 형태를 띄고 있을 때 사용.
• 데이터 구조 관련 알고리즈믜 상당 부분에 재귀 호출이 사용
• 코딩 테스트

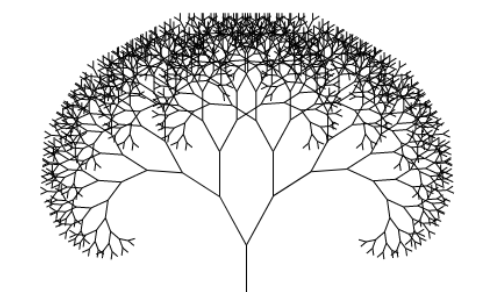
💡 프랙탈(fractal)

• 부분이 전체와 유사한 기하학적 형태(자기 유사성)
  
• 부분을 확대했을 때 전체와 유사한 형태가 등장
• 위그림의 부분들은 트리형태 자료형과 비슷함.

📚 2. 재귀 호출의 예

💡 재귀 호출의 예

• 이진트레에서 노드의 크기

size(u) 
	if u = nil then return 0
    return 1 + size(u.left) + size(u.right)

💡 재귀 함수의 작성

• 문제를 해결하기 위해 풀어야 하는 문제 일부가 크기만 달라지며 원래 문제와 같은 형태를 띄고 있을 때.
  • 문제가 부분 문제들로 어떻게 분활(decompose) 되는지, 보통 다음 경우 (next case) 를 정의.
  • 부분 문제로의 호출이 무한히 반복되지 않도록 기본 케이스 (base case)를 정의.
• 팩토리얼

# n! = n * (n - 1) * (n - 2) ... * 2 * 1
factorial(n)
	if n = 1 then
 		return 1 # base case
       
    else 
    	return n * factorial(n - 1) # next case        

• 피보나치 수열

# 1, 1, 2, 3, 5, 8, 13, 21 ...
# f(1) = 1, f(2) = 2, f(n) = f(n - 1) + f(n - 2)

fib(n)
	if n = 1 or n = 2 then
    	return 1 # base case

	else
    	return fib(n - 1) + fib(n - 2) # next case        

• 부분 함수

# ex) subset([1,2,3])
# => [[], [1], [2], [2, 1], [3], [3, 1], [3, 2], [3, 2, 1]]

subset(seq)
	len_seq ← length(seq)
   
	if len_seq = 0 then
		return [[]] # base case
       
	else
		elem ← seq[0]
       
		rest_sub ← subset(seq[1:])
		return (rest_sub + [[elem] + sub for sub in rest_sub]) # next case

• 🗣️ 재귀 함수를 사용해서 함수를 정의하면 코드가 간단하고 직관적이게 된다는 장점이 있음.

📚 3. 재귀 호출의 효율

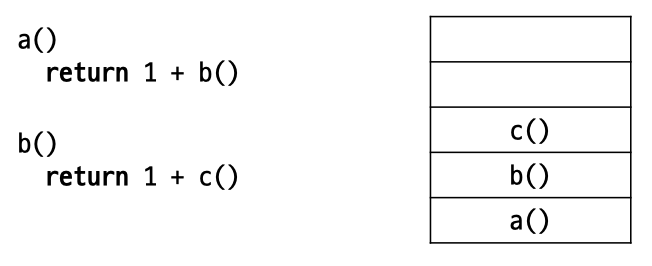
💡 콜 스택

• 함수가 리턴된 뒤, 실행을 재개할 주소를 저장해 놓은 스택
• 함수 a 내에서 다른 함수 b가 호출되면 b가 결과를 리턴한 후, a 함수를 재개해야 하므로 코드 실행을 재개할 부분의 주소를 저장해 놓아야 함.
  
• 호출이 역순으로 실행이 재개되어야 하므로 push된 순서의 역순으로 pop이 일어나는 (LIFO) 스택이 유용함.
• 콜 스택에 주소가 저장될 때마다 메모리상에 공간을 차지함.

💡 재귀 함수에서의 콜 스택

• factorial(5) 가 실행되면 다음과 같이 함수에 호출이 반복적으로 일어나게 되고 콜 스택상에 주소가 계속 담기게 됨.
• 스택 오버플로우(stack overflow) : 콜 스택이 자라나면서 메모리 공간을 모두 소진해 버리면 에러가 발생.

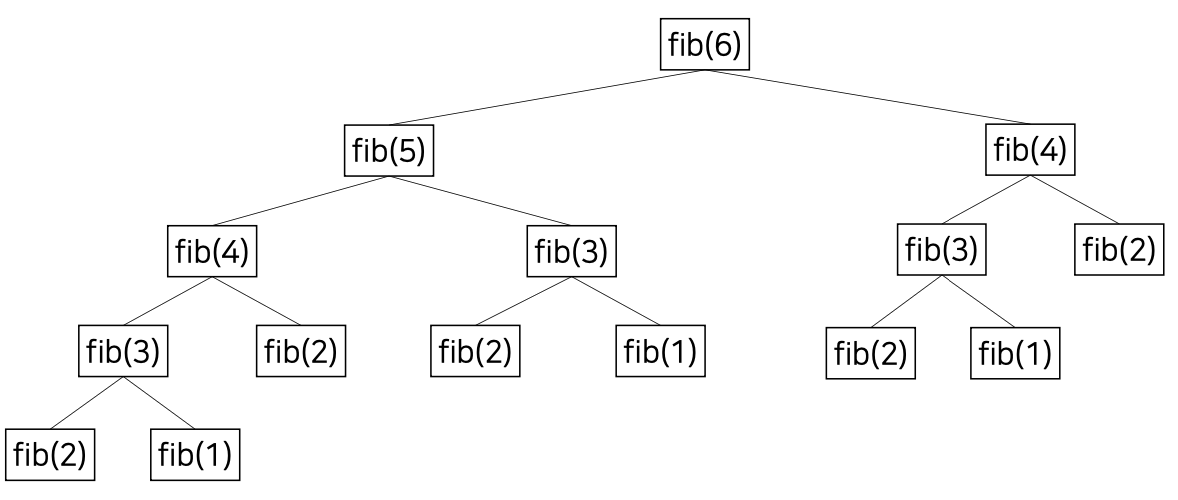
💡 재귀 호출이 비효율적인 경우

• fib(6)을 구하는 경우, fib(3), fib(2) 처럼 같은 연산을 하는 함수가 여러차례 호출되게 됨.
• fib(n)의 n이 커지는 경우 호출수가 지수적으로 증가하게 됨.

📚 4. 동적 프로그래밍

💡 Dynamic Programming

• 재귀를 사용하면 코드가 간단해지고 직관적이라는 장점이 있지만 중복 연산 때문에 비효율이 발생할 수 있음.
• 루프를 사용하거나 메모이제이션 기법을 사용해서 재귀호출의 비효율을 해결하는 방법.
• 광의의 동적 프로그래밍은 주어진 복잡한 문제를 보다 간단한 부분 문제로 분해해서 푸는 접근 방식을 지칭.

💡 동적 프로그래밍이 필요한 경우

• 모든 재귀 호출에 중복으로 인한 비효율이 발생하는 것은 아님.
  • 퀵정렬, 병합정렬 등에서도 재귀호출이 사용되지만 중복이 발생하지 않음.
• 중복으로 인한 비효율이 발생할 때만 동적 프로그래밍이 필요.

📚 5. 루프를 활용한 동적 프로그래밍

💡 루프를 활용한 동적 프로그래밍

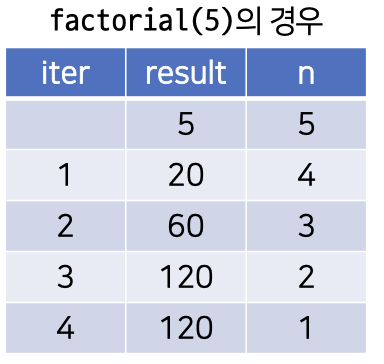
• 팩토리얼 구현

factorial(n)
	result = n
   
    while n > 1 do
    	result = result * (n - 1)
        n = n - 1
       
	result result        

• result, n 두 개의 변수만 메모리에 할당해두고 함수 작동. 따라서 공간적으로 효율적임.

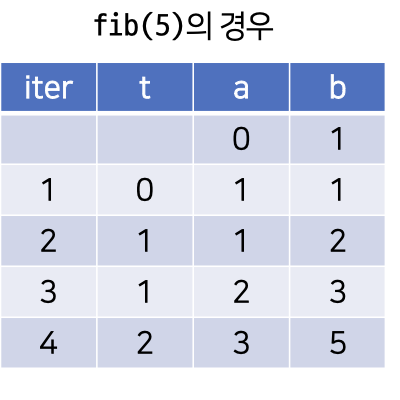
• 피보나치 구현

fib(n)
	a ← 0
	b ← 1
   
    for i in 1,2,...,n-1 do
    	t ← a
        a ← b
		b ← a + t
       
	return b

• n이 아무리 커져도 메모리에 할당되는 변수는 총 3개

💡 루프를 활용한 동적 프로그래밍의 특징

• 중복되는 연산을 없앨 수 있음.
• 재귀적인 호출이 없기 때문에 콜 스택이 많은 공간을 차지하지 않음.
• 재귀 호출을 사용하는 경우에 비해 코드의 직관성이 떨어짐.

📚 6. 메모이제이션을 활용한 동적 프로그래밍

💡 메모이제이션을 활용한 동적 프로그래밍

• 한번 계산한 결과를 저장해 놓고, 같은 계산을 반복해야 하는 순간에 저장한 결과를 재활용하는 것.
• 메모리에 캐시와 비슷한 역할을 함.

• 피보나치 구현

memo ← {} # 메모를 위해서 해시 구조를 사용

	fib(n, memo)
		if n = 1 or n = 2 then
			return 1
           
		if n in memo then
			return memo[n]
           
		else
		memo[n] ← fib(n-1, memo) + fib(n-2, memo)
       
		return memo[n]

💡 메모이제이션을 활용한 동적 프로그래밍의 특징

• 중복되는 연산을 없앨 수 있음.
• 재귀적인 호출이 일어나기때문에 콜 스택 공간이 소요됨.
• 재귀 호출을 사용하는 코드에 계싼 값을 저장하는 변수만 추가하면 되기에 코드가 직관적이게 됨.