정렬1 : (정렬, 선택정렬, 버블정렬, 삽입정렬)

📚 1. 기본적인 정렬

💡 정렬이란?

• 주어진 원소들을 일정한 순서대로 나열하는 것

• 오름 차순 정렬 : 값이 커지는 순서로 정렬.
• 내림 차순 정렬 : 값이 작아지는 순서로 정렬.

📚 2. 선택 정렬

💡 선택정렬 이란?

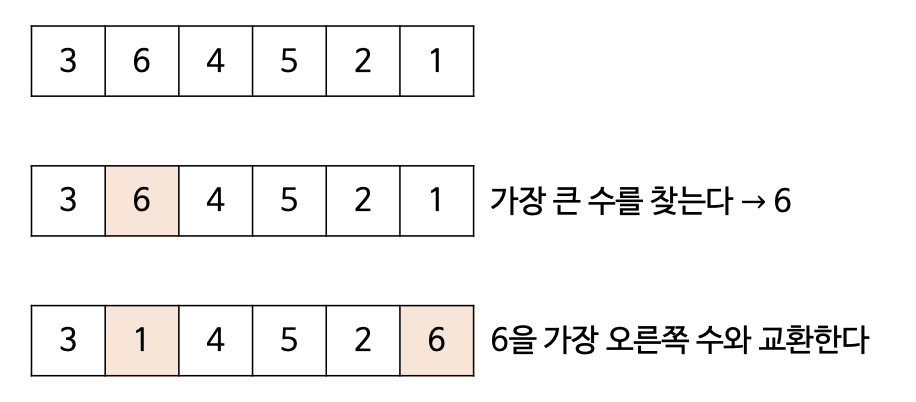
• 가장 큰 원소를 맨 끝으로 보내는 정렬 방식
  
• 위와 같이 가장 큰 수를 찾아 가장 오른쪽으로 보내는 과정을 반복적으로 진행.

💡 선택정렬의 시간 복잡도?

• n개 원소로 이루어진 배열의 가장 큰 수를 찾기 위해 필요한 비교 연산의 수 : n - 1
  • 따라서 시간복잡도 O(n^2)

💡 선택정렬의 구현

selection_sort(a)
	if length(a) ≤ 1 then
		return # base case
       
	n = length(a)
	i = max_index(a)
   
	a[n-1], a[i] ← a[i], a[n-1]
   
	selection_sort(a[:n-1]) # next case

📚 3. 버블 정렬

💡 버블정렬 이란?

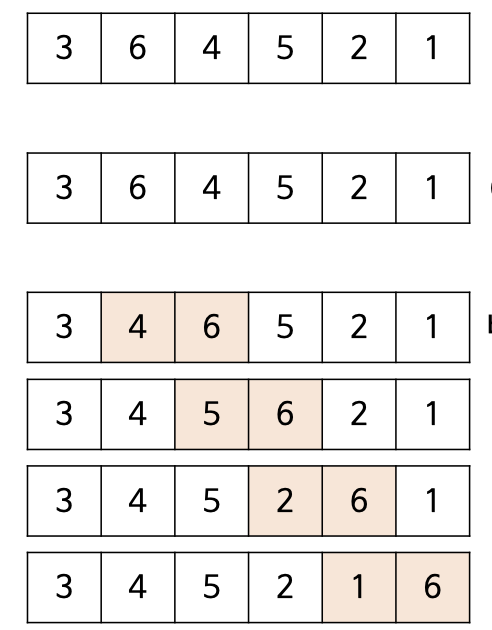
• 두 개의 원소(쌍)을 비교하여 순서가 옳지 않으면 두 원소를 교환하는 것을 반복하는 정렬
• 배열을 따라 원소쌍들을 비교하는 작업을 한 번 끝낼 때마다 가장 큰 원소가 맨 끝으로 옮겨지는 것이 선택정렬과의 공통점
  

• (3, 6), (6, 4) 과 같이 왼쪽으로 이웃한 쌍을 비교하고 이중 순서에 맞지 않는 쌍이 있으면 위치를 교환함.
• 위 경우에는 (6, 4)가 맞지 않으므로 이를 (4, 6)으로 변경해줌.
• 순서가 맞을 때 까지 위 과정들을 반복해줌.

💡 버블정렬의 시간 복잡도?

• 첫번째 루프에서 비교해야 하는 쌍의 수 : n - 1
• 두번째 루프에서 비교해야 하는 쌍의 수 : n - 2
• 세번째 루프에서 비교해야 하는 쌍의 수 : n - 3
• (n - 1) + (n - 2) + ... + 1 = n(n - 1) / 2
  • 따라서 시간복잡도 O(n^2)

💡 버블정렬의 구현

bubble_sort(a)

	if length(a) ≤ 1 then # base case
		return
       
	n = length(a)
   
	for i in 0..n-2 do
   
		if a[i] > a[i+1] then
			a[i], a[i+1] ← a[i+1], a[i]
           
	bubble_sort(a[:n-1]) 

📚 4. 삽입 정렬

💡 삽입정렬 이란?

• 기존에 정렬되어 있는 배열에 새로운 원소를 하나씩 삽입하여 정렬하는 방식
  • 삽입할 때 정렬된 상태가 있는 위치를 찾아서 삽입
    
    

• 순서가 맞을 때 까지 위 과정들을 반복해줌.

💡 삽입정렬의 시간 복잡도?

• 처음 원소를 가져왔을 때 삽입을 위해 필요한 비교 연산 수 : 1
• 두번째 원소를 가져왔을 때 삽입을 위해 필요한 비교 연산 수 : 2
• 세번째 원소를 가져왔을 때 삽입을 위해 필요한 비교 연산 수 : 3
• 1 + 2 + ... + (n - 1) = n(n - 1) / 2
  • 따라서 시간복잡도 O(n^2)

💡 삽입정렬의 구현

insertion_sort(a)
	return _insertion_sort([a[0]], a[1:])
   
_insertion_sort(a, b) # a : 기존에 정렬된 배열, b : 정렬이 필요한 배열
# '_'를 쓰는 이유는 내부적으로 사용하는 함수일 경우이기에
	if b = [] then
		return a
       
	else
		return _insertion_sort(insert(a, b[0]), b[1:])
       
insert(a, elem)
	n = length(a)
   
	if a[n-1] ≤ elem then
		return a + [elem]
       
	if elem ≤ a[0] then
		return [elem] + a
       
	for i in 0..n-2
   
		if a[i] ≤ elem and elem ≤ a[i+1] then
			return a[:i+1] + [elem] + a[i+1:]

📚 5. 이미 정렬된 배열이 주어지는 경우

💡 다음과 같은 배열이 주어졌을 경우 [1, 2, 3, 4, 5, 6]

• 선택 정렬 : 시간복잡도 : O(n^2)
• 버블 정렬 : 시간복잡도 : O(n^2)
• 삽입 정렬 : 시간복잡도 : O(n)

💡 삽입 정렬

• 삽입 정렬은 완벽히 정렬된 배열이 아니더라도, 정렬에 가까운 상태인 배열이 주어질 수록 O(n)에 가까운 성능을 냄.