정렬2 : (힙정렬, Heapify 알고리즘, 퀵정렬, 병합정렬)

📚 1. 힙정렬

💡 힙정렬이란?

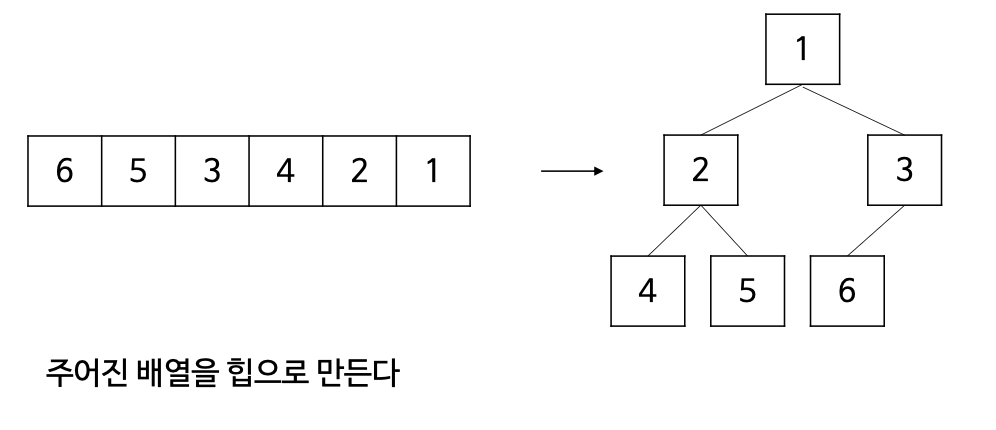
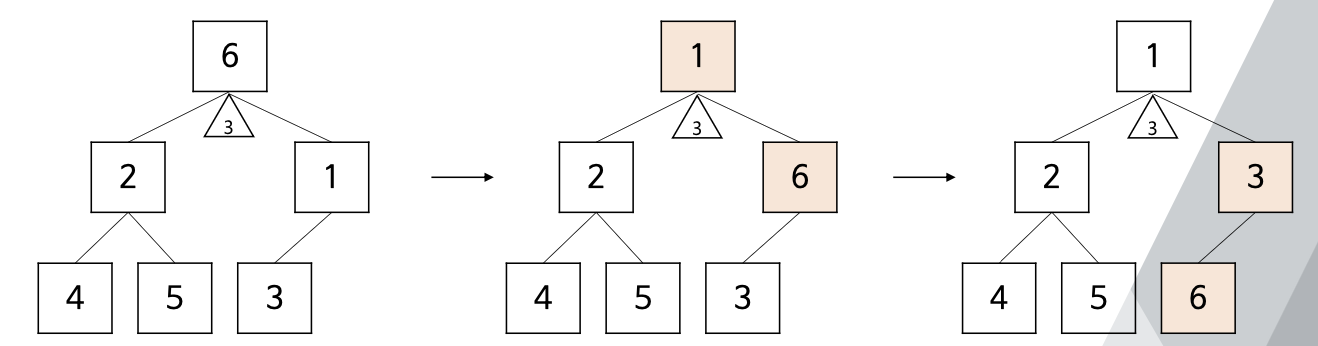
• 주어진 배열을 최소힙으로 만든 뒤, 힙에서 원소들을 하나씩 제거하며 정렬을 수행하는 방법는 것
  
  
  

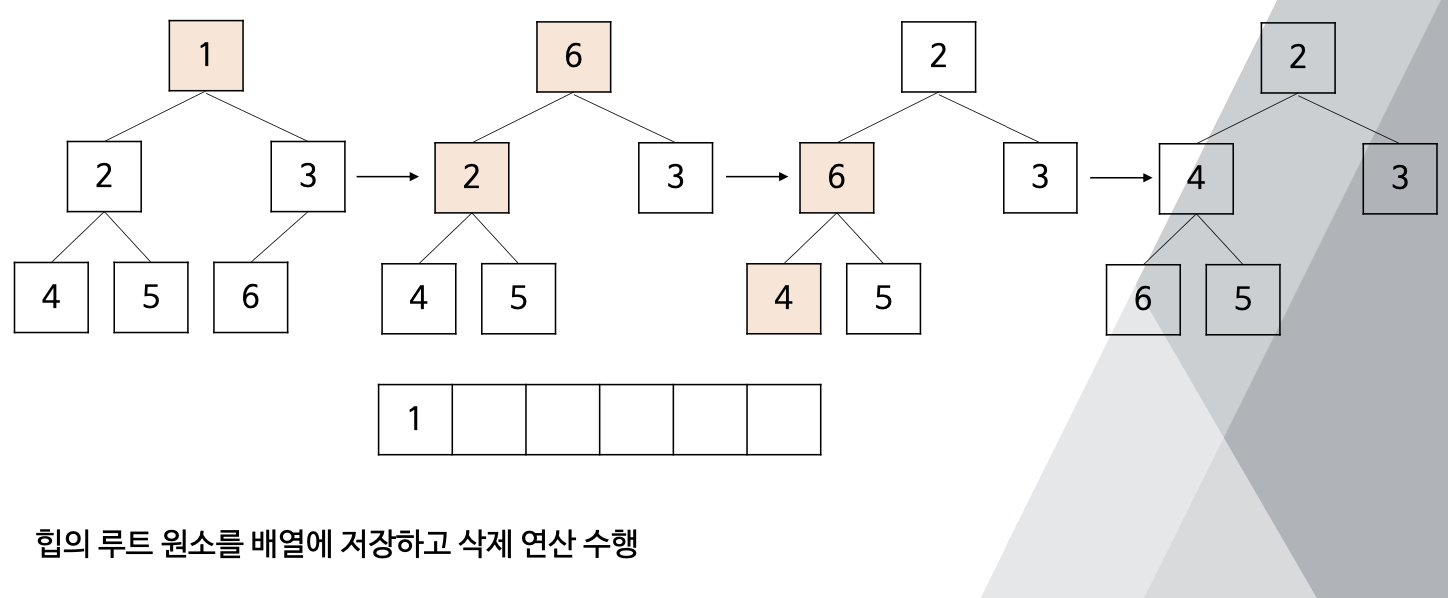
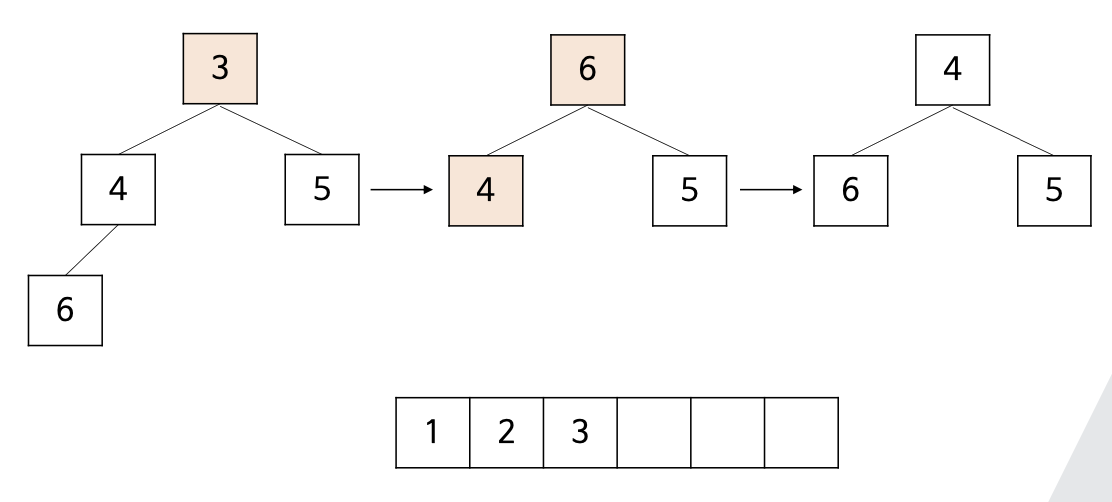
• 반복적으로 힙의 루트 원소를 배열에 저장하고 삭제 연산 수행

💡 힙정렬의 시간 복잡도?

• 힙 삭제 연산의 시간 복잡도 : O(logn)
• 정렬을 수행하기 위해 수행하는 삭제 연산의 횟수 : n
• 힙정렬의 시간 복잡도 : O(nlogn)
• 이 시간 복잡도는 힙의 생성에 소요되는 시간 복잡도는 힙의 생성에 소요되는 시간은 고려하지 않음.

💡 힙의 생성

• William's method
  • n개의 배열 원소에 대해 차례로 힙의 삽입 영ㄴ산을 수행하면 힙을 성생할 수 있음.
  • 힙의 삽입 연산의 시간 복잡도 : O(logn)
  • 힙의 생성에 필요한 시간 복잡도 : O(logn)
• 힙의 생성을 고려해도 힙정렬의 소요되는 시간 복잡도는 O(logn).

📚 2. 힙정렬을 구현하는 Heapify 알고리즘

💡 Heapify 알고리즘

• William's method 보다 효율적인 알고리즘
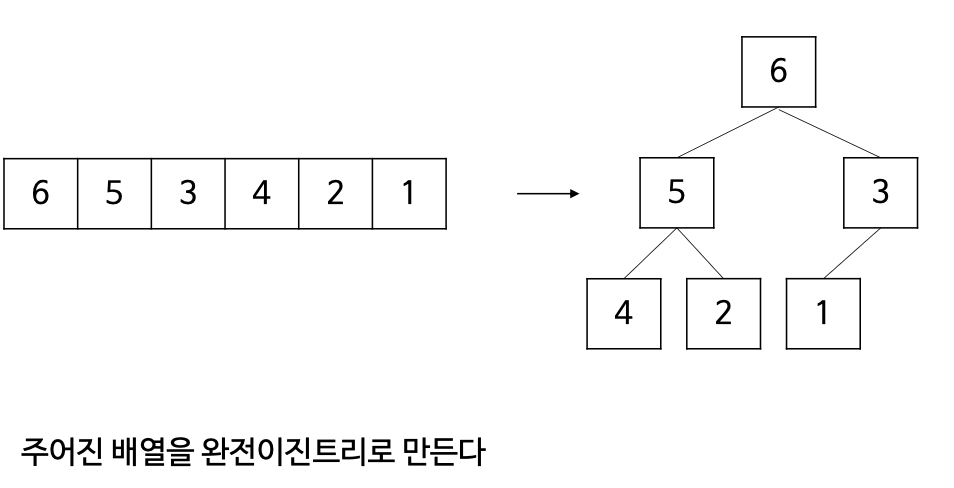
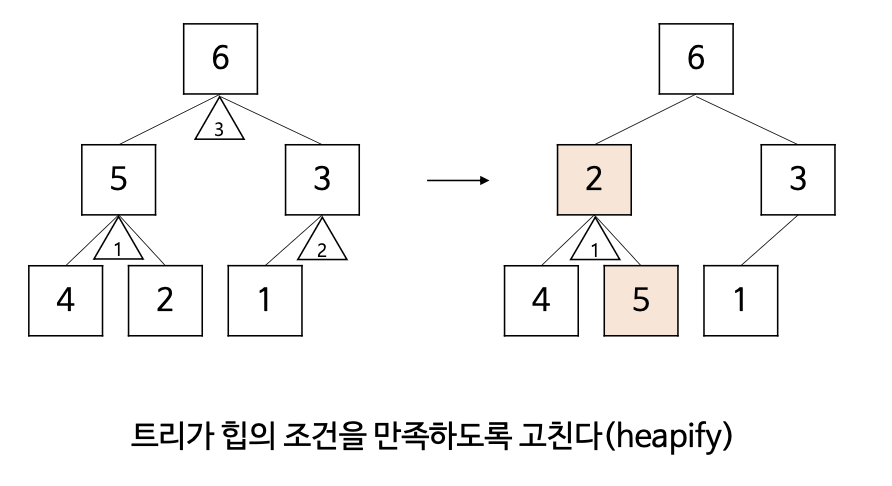
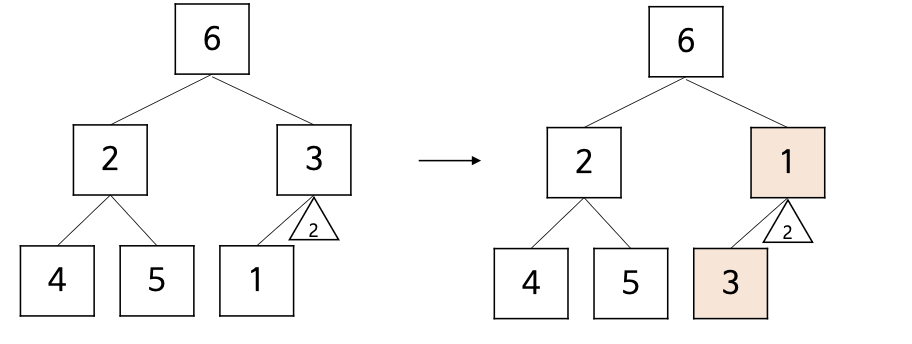
• 배열을 이진 트리로 바꾼뒤 이진트리가 힙의 조건을 만족하도록 수선.
  
  
  
  

• 각각의 서브트리가 힙정렬을 만족시키도록 가장 아래 레벨에 왼쪽에서부터 수선해 나가는 과정.

💡 Heapify 알고리즘의 시간 복잡도?

• subtree의 수 = subtree의 root 수 = leaf를 제외한 모든 노드 수 = n / 2
• trickle_down의 시간 복잡도 : O(logn)
• 최악의 경우 O(logn)이 되는 것처럼 보이지만, 아래 레벨의 subtree일수록 높이가 작아 trickle_down에 걸리는 시간이 O(logn)보다 작기에 Heapify의 시간 복잡도는 O(n)이 됨.
• 그러나 힙이 생성되는데 O(n)이 소요되더라도 힙정렬을 수행하는데 걸리는 시간은 O(logn)이므로 최악의 결과를 상정하는 bigO에 따라 결론적으로는 힙정렬은 O(logn)이 소요됨.

📚 3. 퀵정렬

💡 퀵정렬이란?

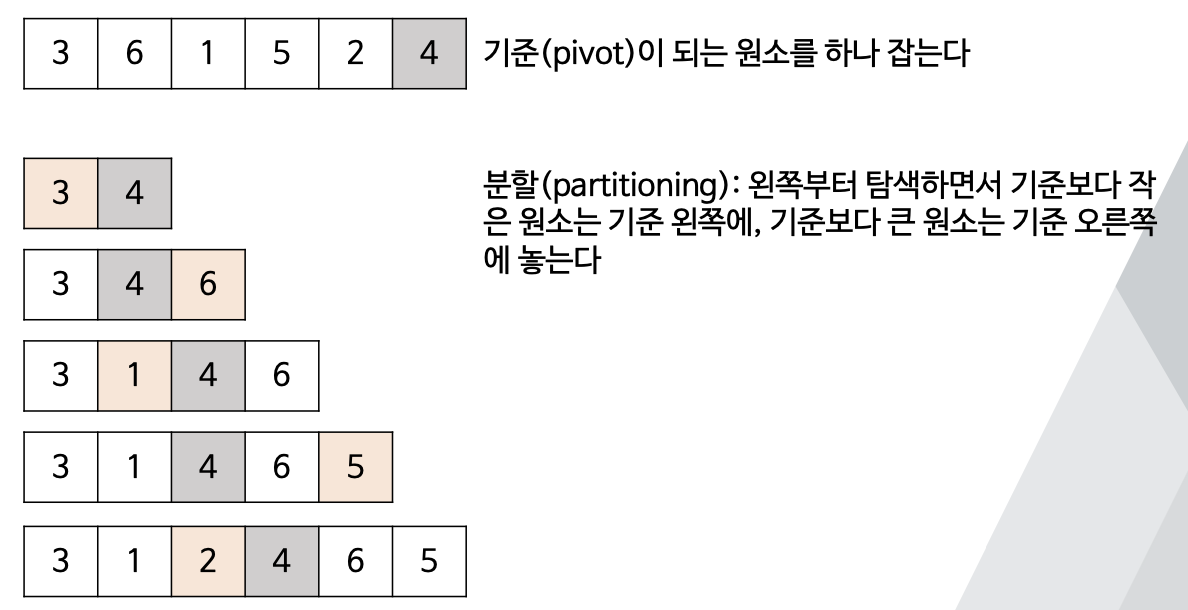
• 선택한 원소를 기준으로 배열을 두 부분으로 분할한 뒤, 분할한 배열들에 대해 재귀적으로 퀵정렬을 호출하여 정렬.
  

• 위에서 기준으로 잡은 4를 기준으로 왼쪽 배열과 오른쪽 배열로 나눈 후 다시 퀵정렬을 재귀적으로 호출함.
  
  

💡 퀵정렬의 시간 복잡도?

• 최악의 경우 : 분할시 한쪽에만 원소가 몰리는 경우가 반복되는 경우 = O(n^2)
  • 지속해서 가장 큰 원소가 정렬 기준으로 사용되는 경우
• 평균적인 경우 : 분할 시 양쪽의 원소 수가 비슷한 경우 = O(nlogn)
  • 중간 값에 원소가 정렬 기준으로 사용되는 경우
• 따라서 평균적으로 O(nlogn)으로 가장 좋은 성능을 내기 때문에 실무에서 가장 많이 사용됨.

💡 선택정렬의 구현

quicksort(a)

	if length(a) ≤ 1 then
		return a
       
	pivot ← a[0]
	left, right ← partition(a, pivot)
   
	return quicksort(left) + [pivot] + quicksort(right)

📚 4. 병합정렬

💡 병합정렬이란?

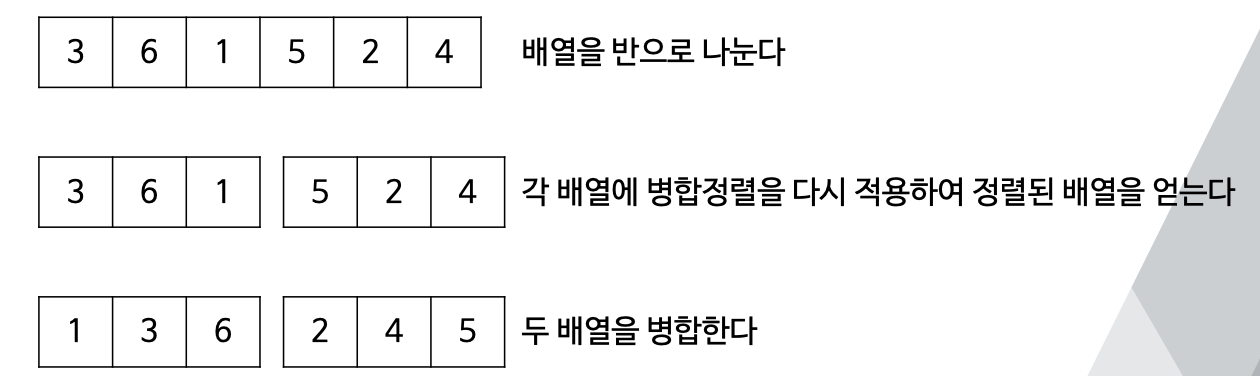
• 배열을 반으로 나누어 각 부분에 대해 병합정렬을 재귀적으로 호출 후, 나누어진 부분을 병합하여 정렬을 완성하는 방법.
  
  

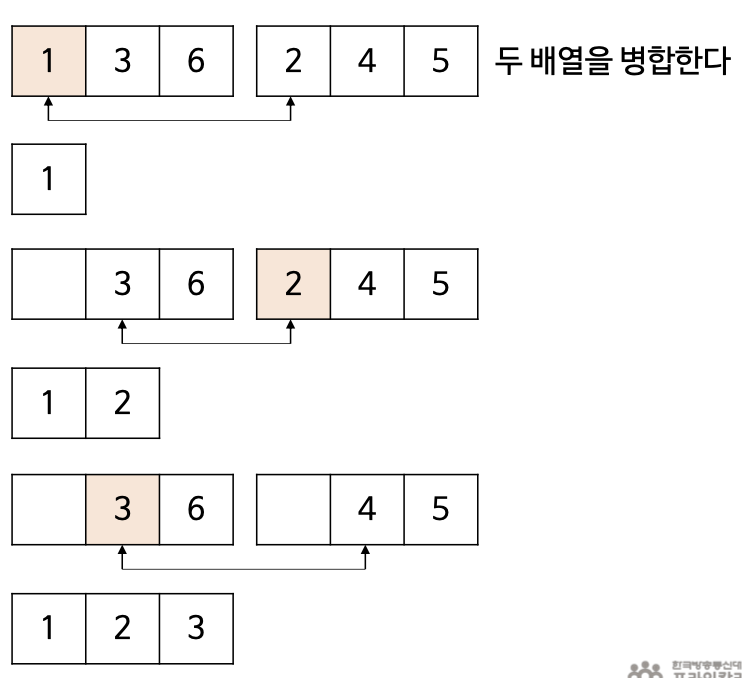
• 배열을 병합하는 방법은 각 배열에서 맨 앞에 있는 원소를 비교 후 더 작은 값을 정렬배열에 추가
• [1,3,6][2,4,5] 에서 우선 (1, 2) 를 비교 후 더 작은 1을 정렬배열에 추가 그 후 (3, 2) 비교... 이 방식으로 계속해서 정렬배열에 추가

💡 병합정렬의 시간 복잡도?

• O(nlogn)
  • 병합 시 비교연산 수 : n
  • 필요한 병합 수 : logn

💡 병합정렬의 구현

merge_sort(a)

	if length(a) ≤ 1 then
		return a
       
	mid ← int(length(a) / 2)
	left ← merge_sort(a[:mid])
	right ← merge_sort(a[mid:])
   
	return merge(left, right)