배우면서 쓰는 암호학

사실 지금까지 설명한 모든 암호 체계는 블록 암호화 체계, 즉 대칭키 암호 체계이다. 대칭키 암호 체계는 송신자와 수신자가 모두 같은 암호 키를 공유하고 있어야 사용이 가능한데, 이런 암호 키 공유 과정에서 공격이 들어온다면 이는 암호화라고 할 수 없게 된다.

이번 포스팅에서는 이런 암호 키 공유 시스템 중에서 가장 널리 쓰이고 있는 Diffie-Hellman 공유 시스템에 대해서 알아보고자 한다.

- Diffie-Hellman -

이 알고리즘을 설명하기에 앞서, 먼저 크게 3가지의 수학적 지식이 필요하다

• mod 거듭제곱 계산
• Fermat's little theorem
• Discrete Logarithm Problem

앞의 두 지식은 굳이 설명할 필요 없지만, 마지막 이산 로그 문제는 몇가지 알고 넘어가야 할 필요성이 있다.

>> 이산 로그 문제

이산 로그 문제는 쉽게 말해서, 주어진 a,b,n 정수가 존재할 때,
a^x ≡ b (mod m) 를 만족하는 x를 찾는 것을 말한다.

한 가지 예시로, a = 5, b = 52, n = 61 이라고 가정해보자. 여기서 x의 값을 구하기 위해서는 프로그래밍으로 하나하나 입력해보며 찾아낼 수 있다. 아마 어렵지 않게 만족하는 x의 값이 21이라는 것을 확인할 수 있다.

하지만, 만약 b와 n 의 수가 매우매우 커지게 되면 어떤 일이 발생할까? 아마 엄청나게 많은 경우의 수를 탐색해야 하기 때문에 매우 힘든 과정이 될 것이다.

이런 특성을 이용해서 Diffie-Hellman 알고리즘을 만들어내게 되는데, 이제 이 알고리즘이 무엇인지 알아보도록 하자.

>> Diffie-Hellman Algorithm

먼저, 거두절미하 먼저 그림을 보도록 하자.

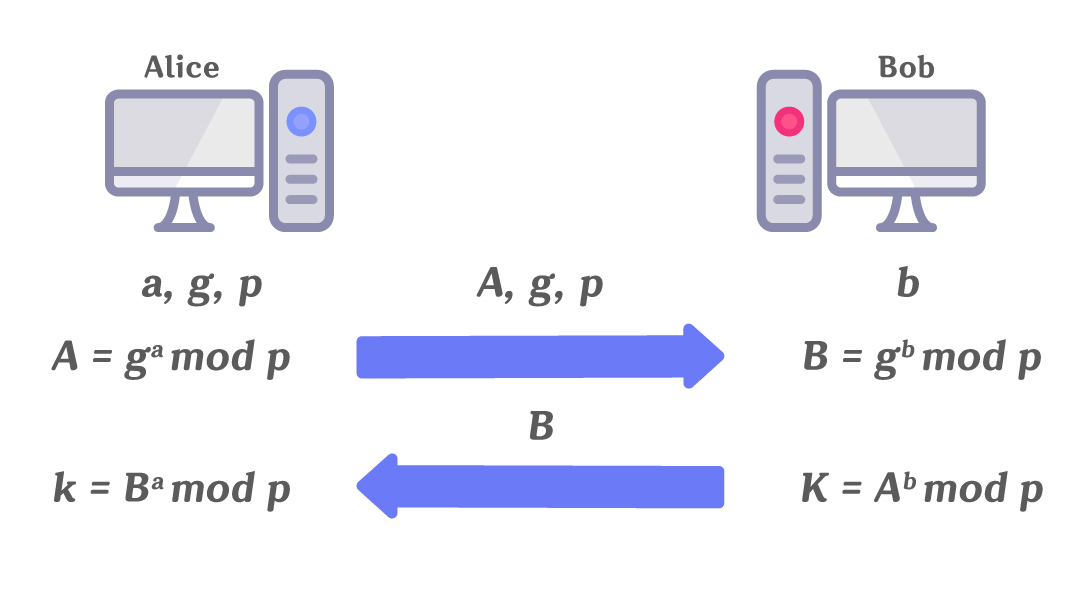
먼저, 총 5가지 단계로 이루어진다. 살펴보자.

• 송신자 Alice가 임의의 매우 큰 소수 P를 정하고, 그 p보다 작은 a와 g를 정하게 된다.

• 송신자는 수신자 Bob에게 A, g, p를 송신하게 된다. (여기서 A는 위의 그림에 나와 있는 수식이다.)

• 수신자 Bob은 얻은 P와 g를 토대로, 새로운 p 보다 작은 b 라는 정수를 정의하고, B를 송신자에게 다시 보내게 된다.

• 결국 송신자 Alice는 a,g,p,B 를 알고 있고, 수신자는 A,g,p,b를 정보로 가지게 된다.

• Alice는 B의 a제곱을 계산하고, Bob은 A의 b제곱을 계산하게 되는데, 사실상 이 두 값은 동일한 값이다.

이런 방식으로 서로 같은 값을 공유하게 된다.

여기서 공격자가 중간에서 정보를 가로채간다고 해도, 공격자가 얻을 수 있는 정보는 p, g, A, B로 제한되어 있다. 하지만 이산 로그 문제에 의해서 A, B를 이용해서 a, b 를 구할 수 없기 때문에 결국 공격자는 송신자와 수신자가 공유하는 값을 가질 수 없게 된다.

>> 취약점

하지만, 모든 보안 기법에는 취약점이 존재한다. 이 완벽해 보이는 Diffie-Hellman 알고리즘도 취약점이 있는데, 이를 알아보도록 하자.

중간자 공격

중간자 공격은 두 컴퓨터가 통신하는 동안, 중간에 끼어들어 정보를 조작하거나 가져오는 행위를 말한다. 이런 중간자 공격에도 2가지가 있는데, 직접적으로 끼어드는 능동적 공격, 그리고 간접적으로 끼어드는 수동적 공격이 있다.

그래도 수동적 공격은 도청과 같이 정보를 입력받는 행위밖에 하지 못한다. 따라서 수동적 공격을 한다고 해도 위의 Diffie-Hellman 알고리즘에 영향을 주지 못한다.

하지만, 능동적 공격은 두 컴퓨터 사이에 위치해 정보를 변조할 수도 있다.

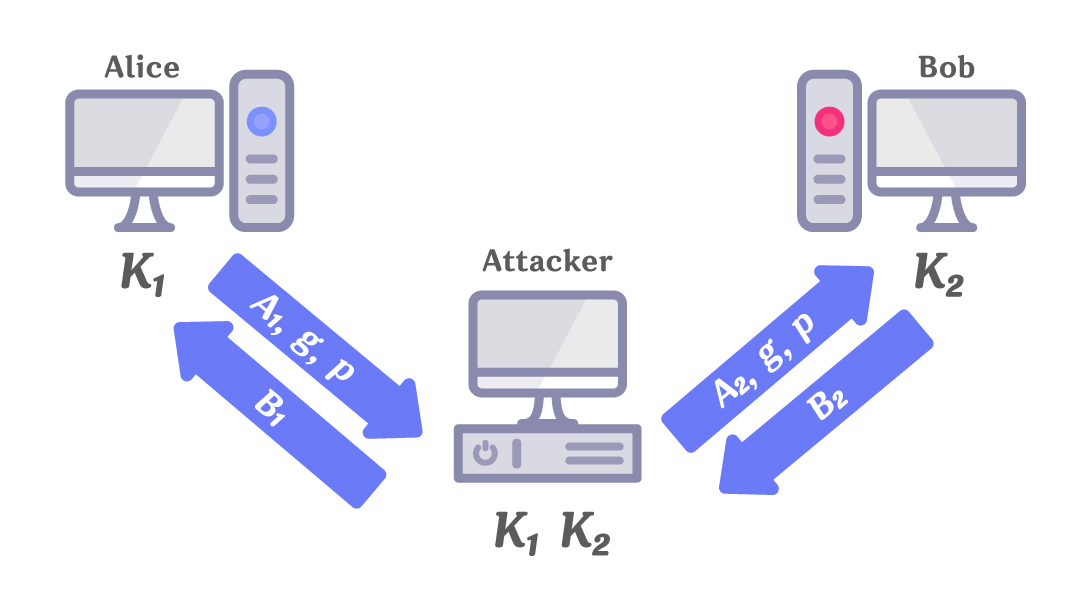
위의 그림과 같이 공격자는 A의 값을 변조해서 수신자에게 넘겨주고, B의 값도 변조해서 송신자에게 넘겨줄 수 있다.

결국 이 과정을 겪으면 중간자 공격에 취약점이 노출되어 모든 정보이 노출되게 된다. 이 중간자 공격을 막기 위해서 나중에는 신원 확인을 위한 과정이 생긴다. 이 과정은 나중에 포스팅하도록 하겠다.

---