배우면서 쓰는 암호학
이번에는 암호학의 꽃, RSA 암호에 대해서 알아보도록 하자.
지금까지 암호와 관련된 수학을 배워오면서, 도대체 어떻게 이 수학 이론이 암호 체계에 쓰이는지 몰랐는데, 이번 RSA 암호를 공부하고 나니 그 궁금증이 해결되었다.
과거부터 현재까지 엄청난 천재들이 만들어낸 암호인 RSA 암호에 대해서 알아보도록 하자.
- RSA -
RSA 알고리즘은 비대칭키 암호 시스템 을 사용하고 있다.
이 암호에 대해서 다시 한번 상기하자면, 비대칭키 암호 시스템은 공개키와 개인키 모두를 사용한다. 공개키는 불특정 다수에게 공개하는 key 이고, 개인키는 자신만 가지고 있는 private 한 키이다.
자세한 내용은 다음 포스트를 참고하자.
- Before RSA.. -
RSA 알고리즘은 오일러 정리를 전제로 정의된다.
오일러 정리란, 어떤 정수 n 에 대해서 n 과 서로소인 a 가 다음 식을 만족한다는 정리이다.

그렇다면, 이 오일러 정리는 어떤 식으로 RSA 암호 체계에 활용될까??
먼저 KEY 를 생성하는 알고리즘부터 살펴보자.
- Algorithm -
KEY 는 위에서 언급한 대로, 공개키와 개인키 총 2 종류의 키를 생성하게 된다.
먼저, 키의 생성 과정들부터 살펴보자.
1. 임의의 두 소수 p, q 정의
2. N = p * q 로 N 정의
3. φ(N) 과 서로소인 e 정의 ( 여기서 φ(N) = (p - 1) (q - 1) )
4. d≡e^−1 (mod φ(n)) 를 만족하는 d 정의 <-> d x e ≡ 1 (mod φ(n))
여기서, N 과 e 는 공개키 ( public Key ) , d 는 개인키 ( private Key ) 로 쓰인다.
이 두 종류의 Key 가, 아래의 과정으로 암호화와 복호화가 가능하게 된다.
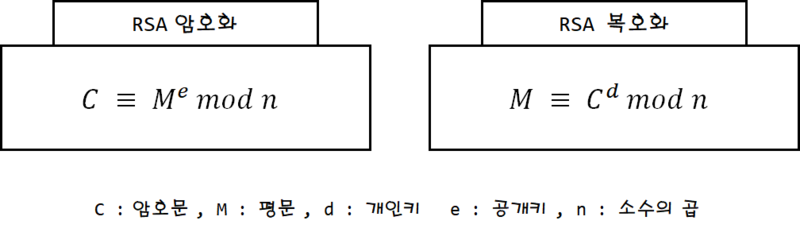
그런데, 여기서 생각할 점은, 과연,, e 랑 N 이 모두 주어졌는데, d 도 그럼 이 연산의 역연산을 통해서 구할 수 있지 않을까?? 라는 점이다.
결론부터 말하자면, 불가능하다.
이전에도 언급한 적이 있지만, N 을 소인수분해하기는 매우 어렵다. 매우 큰 소수 2개를 곱하여 만들어진 정수이기 때문에, 소인수분해하기는 매우 어렵다. 따라서 공개키 N 과 e 를 안다고 해도, d 를 알아내기에는 매우 어렵다.
- RSA Attack -
자, 그렇다면 어떻게 이 RSA 암호를 우회하여 알아낼 수 있을까??
먼저, RSA 암호는 앞서 설명했던 여러 암호와 비교해서 속도가 현저히 느리다. Big num 의 연산과정, 그리고 거듭제곱을 여러 번 하기 때문에 속도가 느려질 수밖에 없다.
자 이 점을 보완(?) 은 아니지만 해소하기 위해서 몇몇 RSA 암호에는 작은 e 를 설정하는 경우가 있다.
바로 이 점 때문에 RSA 암호에 취약점이 생긴다.
- Coppersmith Attack -
이 공격은 엄청난 수학적 개념을 요구한다. 필자도 이 공격기법에 대해서 완벽하게 이해하지 못했기 때문에 설명이 미숙할 수 있다.
이 공격은 앞서 말했던 작은 e 때문에 생기는 취약점을 전제로 한다.
먼저, Coppersmith 정리는
차수가 e인 함수 f(x)에서 찾고자 하는 근이 n^{1/e} 보다 작을 경우, 복잡도가 O (log n) 인 알고리즘을 이용하여 근을 구할 수 있다.
라는 정리이다.

- dreamhack 강의 중 일부라고 하는데, 솔직히 무슨 뜻인지는 잘 모르겠다. dreamhack에서도 굳이 비중을 둔 내용은 아니기에 '이런 공격기법도 존재하는구나~' 라고만 알아두고 넘어가도 될 것 같다.
- Hastad's Broadcast Attack -
이 공격기법도 마찬가지로, 작은 e 를 설정했을 때 발생하는 취약점을 전제로 한다.
이 공격기법은, 한 송신자가 여러 명의 수신자에게 동일한 e 값을 사용했을 때 가능한 공격기법이다.
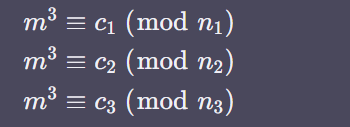
그럼 위의 사진과 같이 나타낼 수 있게 된다. 그럼 여기서 떠올릴 수 있는 하나의 정리가 있다. 바로 CRT, 즉 중국인의 나머지 정리이다. 이 정리를 모른다면 다음의 링크로 가보자.
고로, 
다음과 같은 식을 만들어낼 수 있겠다.
여기서, 우리가 주의해야 할 점은, m 은 각각의 n 보다 작다는 것이다. 따라서, 위의 식에서 mod 를 빼도 만족한다는 결론이 나온다.
따라서 다음과 같은 식이 만들어지게 된다.
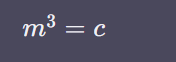
이런 결론을 이용해서, 우리는 쉽게 m 의 값이 무엇인지를 예측할 수 있게 된다.
- Common Modulus Attack -
이 공격은 공통의 n 을 사용했을 때 가능한 공격법이다.
어떤 송신자가, 같은 n, 그리고 서로소인 e1, e2 를 이용해서 c1, c2 의 암호문을 생성했다고 가정하자.
그러면, 우리는 유클리드 확장 알고리즘을 이용해서 r x e1 + s x e2 = 1 이 되도록 r 과 s 를 설정해줄 수 있다. ( 여기서 r 과 s 중 하나는 음수, 하나는 양수가 될 것이다.)
그렇다면, 우리는 c1의 역수나 c2 의 역수만 알아낸다면 다음과 같은 방법으로 평문을 다시 계산할 수 있게 된다.
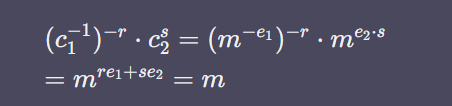
- After -
앞서 말한 공격기법들 때문에, 보통 RSA 암호 체계를 이용할 때, e 의 값을 0x10001 로 고정시켜놓는 경우가 많다.
dreamhack 에서 예제로 준 TextBook-RSA 라는 문제로 이를 감안해서, e 의 값을 65537 ( 0x10001 ) 로 고정시켜 주었다.
dreamhack 의 문제 풀이를 velog 에다 올릴 수 없는 관계로, 각자 문제들을 풀어보기를 바란다.