피마 인디언 당뇨병 예측 분류

박동현·2024년 12월 8일

1. 문제 정의 및 기획

많은 사람들이 데이터 분석을 공부할 때 피마 인디언 당뇨병 예측으로 시작한다.
나도 본격적으로 데이터 분석을 공부 해보기로 했다.

미국 애리조나주 그랜드캐년에서 사진을 찍으면 가장 잘 나오는 위치인 피마포인트는 그 지역에 살고 있는 인디언 부족 피마의 이름에서 유래한 것이다.

피마 포인트의 경관

피닉스대 연구팀은 1979년에 피마 인디언의 당뇨병 유병률이 다른 어떤 인구 집단보다 높다는 논문을 발표했다. 미국 미네소타주 로체스터와 비교하면 19배나 높을 정도였다.

아메리카 대륙의 인디언들은 조상들이 유라시아 대륙에서 베링해를 거쳐 넘어왔다. 춥고 음식이 부족한 상태에서 목적지도 확실치 않은 채 베링해를 넘어오는 것은 목숨을 건 여정이었다. 음식이 부족한 상태에서 음식을 섭취할 기회가 생기면 저장해 놓아야만 가혹한 환경 조건을 이겨낼 수 있었으므로 저장 능력을 키운 이들만 살아남을 수 있었을 것이다.

연구팀은 멕시코 피마 인디언의 생활 방식이 애리조나에서와 유사해지기 시작하면서 멕시코 피마 인디언의 비만과 당뇨병 유병률이 증가하고 있음을 발견했다. 두 집단이 제2형 당뇨병을 유발할 수 있는 유전자를 공통적으로 가지고 있지만 생활습관의 차이가 비만과 당뇨병 발병에 차이를 가져온 것이다.

인용 : https://m.dongascience.com/news.php?idx=66211

2. 데이터 수집

데이터셋은 캐글의 Pima Indians Diabetes Database를 받았다.
출처 : https://www.kaggle.com/datasets/uciml/pima-indians-diabetes-database

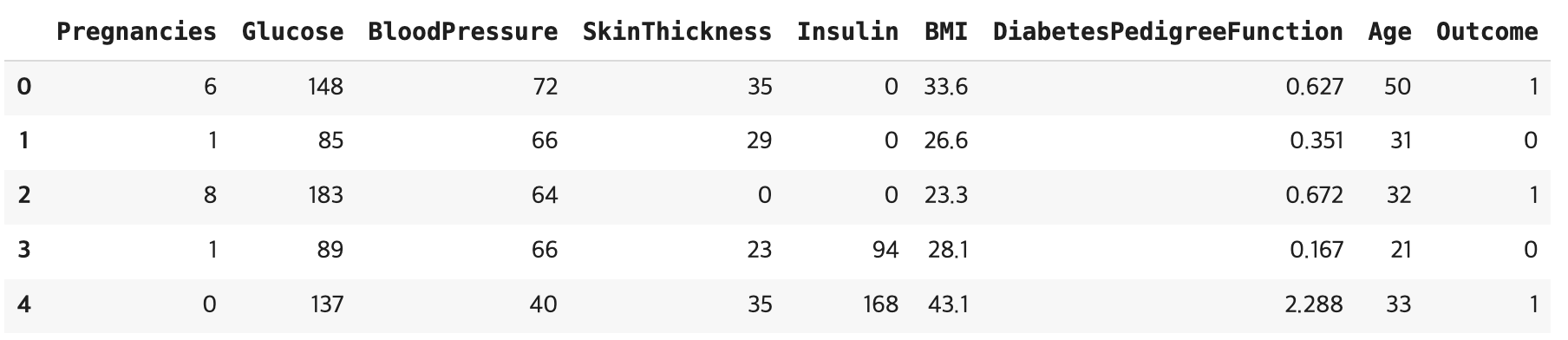
import pandas as pd
data = pd.read_csv("/content/diabetes.csv")
data.head()
데이터셋 확인

Pregnancies: 임신 횟수
Glucose: 포도당 부하 검사 수치
BloodPressure: 혈압(mm Hg)
SkinThickness: 팔 삼두근 뒤쪽의 피하지방 측정값(mm)
Insulin: 혈청 인슐린(mu U/ml)
BMI: 체질량지수(체중(kg)/키(m))^2
DiabetesPedigreeFunction: 당뇨 내력 가중치 값
Age: 나이
Outcome: 클래스 결정 값( 0 또는 1 )

3. 데이터 분석 및 인사이트 도출

data['Outcome'].value_counts()
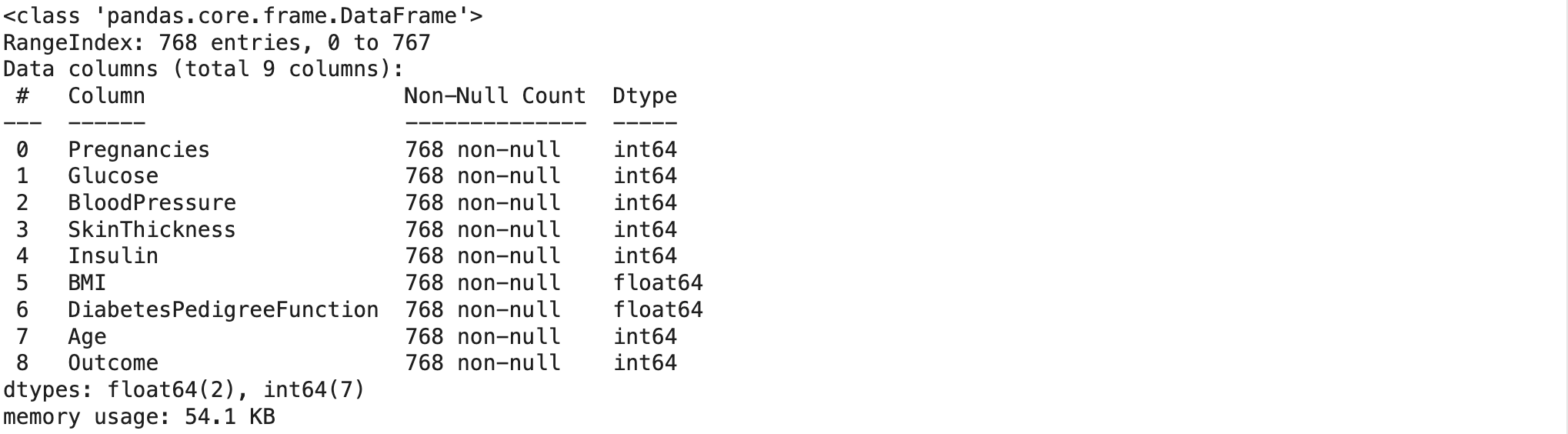
음성이 양성보다 상대적으로 많다.
data.info()
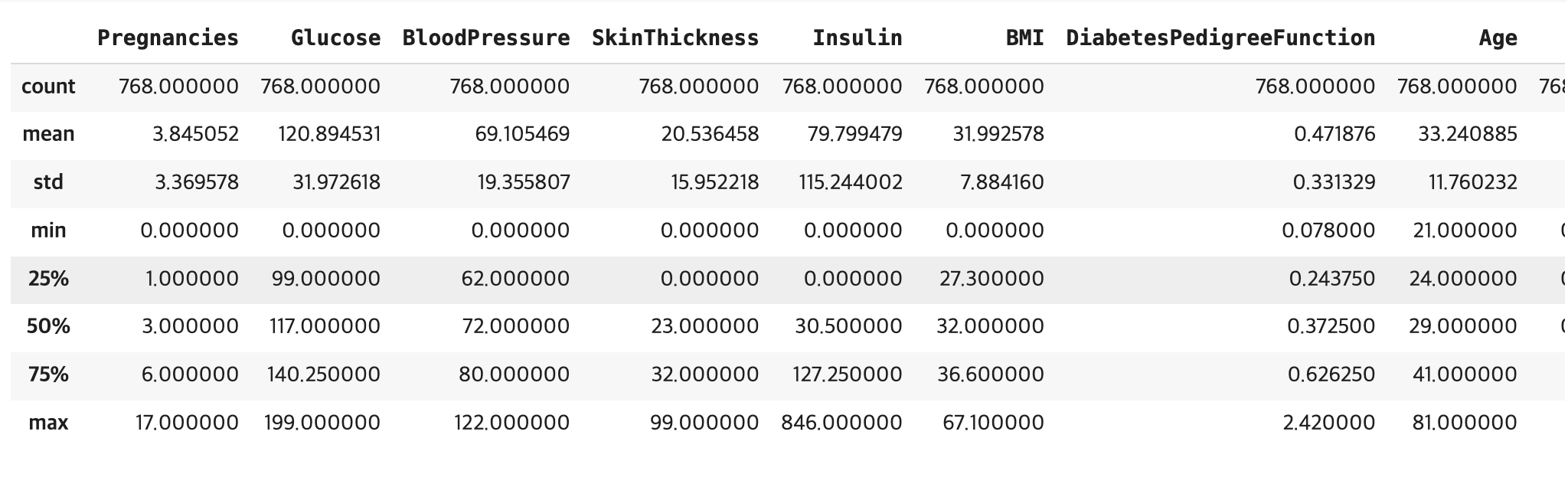
모두 768개의 값으로 결측값은 존재하지 않는다.
data.describe()
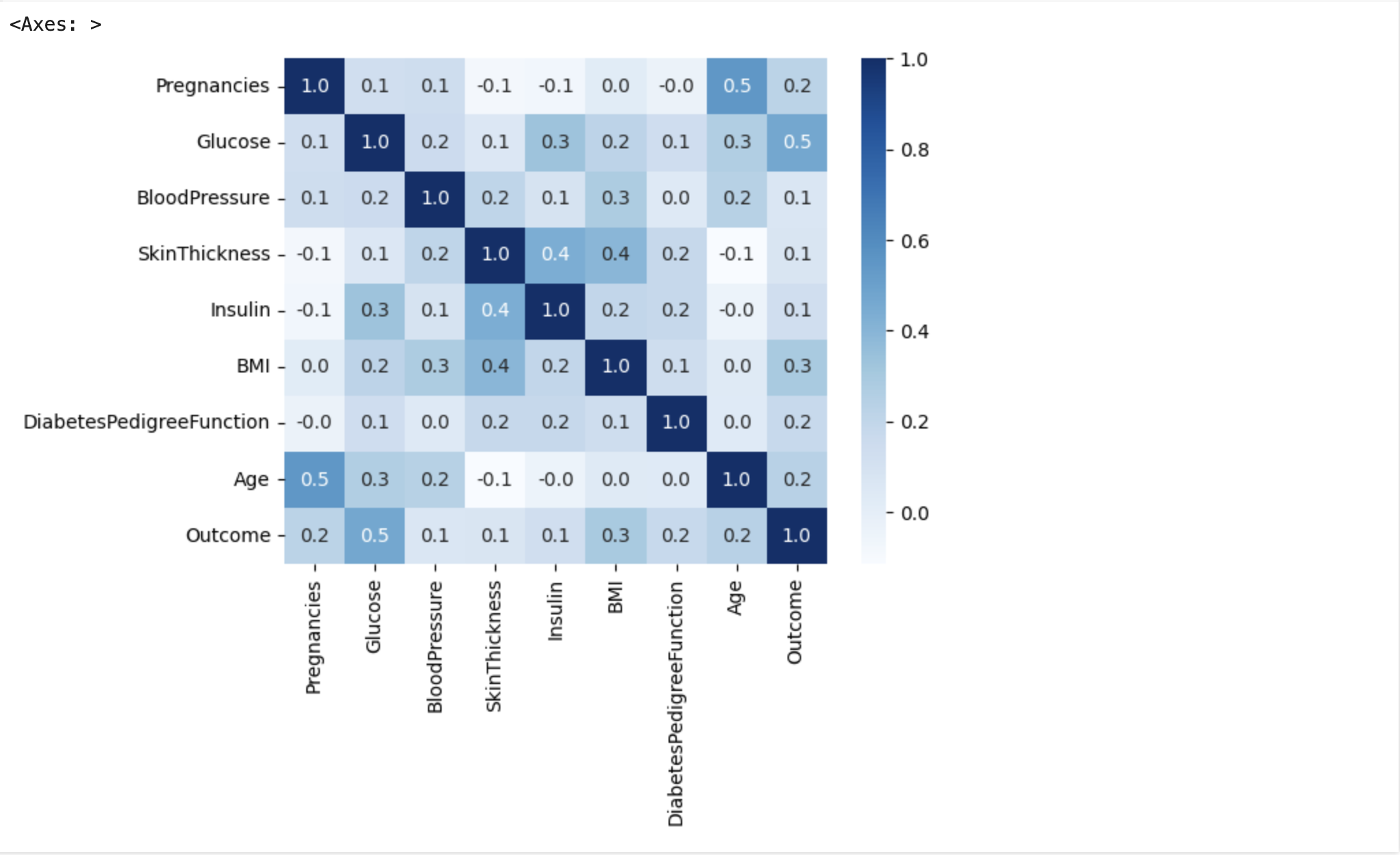
BMI 지수의 평균이 32에 육박하는데 이는 과체중에 해당하는 범위이다.
import seaborn as sns
correlation_matrix = data.corr()
sns.heatmap(correlation_matrix, annot=True, cmap='Blues', fmt='.1f')
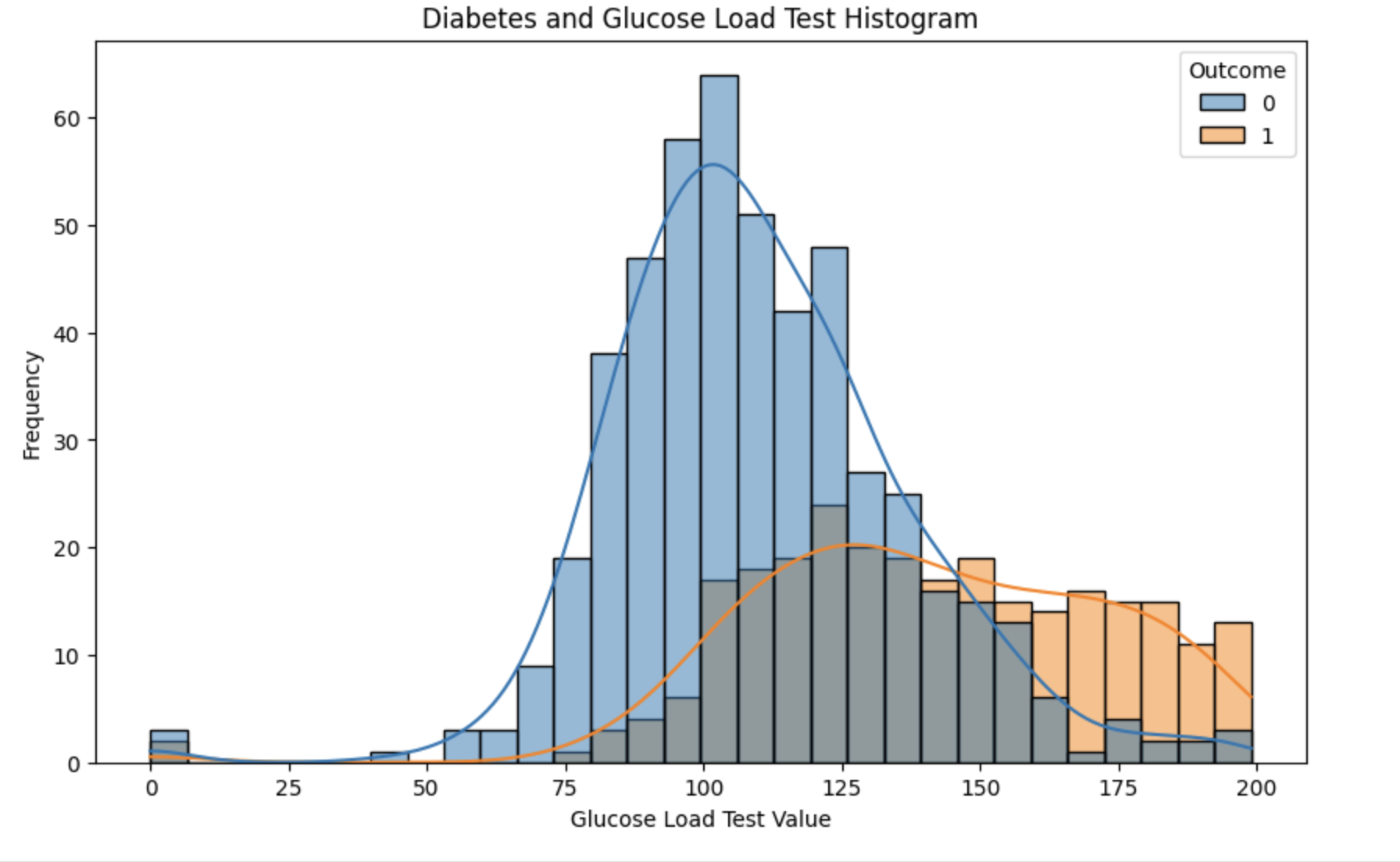
상관관계 히트맵을 그려본 결과, 당뇨병과 포도당 부하 검사 수치가 가장 큰 상관관계를 갖는 것을 알게 되었다.
import matplotlib.pyplot as plt
import seaborn as sns
plt.figure(figsize=(10, 6))
sns.histplot(data=data, x='Glucose', hue='Outcome', kde=True, bins=30)
plt.title('Diabetes and Glucose Load Test Histogram')
plt.xlabel('Glucose Load Test Value')
plt.ylabel('Frequency')
plt.show()
음성군들은 포도당 부하 검사 수치 50 ~ 130 정도의 밀집해있고, 양성군들은 130이상을 넘기고 밀집해있다.

4. 모델 학습

로지스틱 회귀를 사용하여 예측해보기로 했다.

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
x = data.iloc[:, :-1]
y = data.iloc[:, -1]
train_input , test_input, train_target, test_target = train_test_split(x, y, test_size=0.2, stratify=y)
lr = LogisticRegression(max_iter=500)
lr.fit(train_input, train_target)

5. 모델 평가 및 개선

평가함수

from sklearn.metrics import confusion_matrix, accuracy_score, precision_score, recall_score, f1_score, roc_auc_score
def get_clf_eval(test_target, pred=None, pred_proba=None):
    confusion = confusion_matrix(test_target, pred) #혼동행렬
    accuracy = accuracy_score(test_target, pred) # 정확도
    precision = precision_score(test_target, pred) # 정밀도
    recall = recall_score(test_target, pred) # 재현율
    f1 = f1_score(test_target, pred) # F1 점수
    if pred_proba is not None:
        roc_auc = roc_auc_score(test_target, pred_proba[:, 1])  # ROC AUC (예측 확률 사용)
    else:
        roc_auc = roc_auc_score(test_target, pred) 
    print("Confusion Matrix:\n", confusion)
    print("Accuracy: ", accuracy)
    print("Precision: ", precision)
    print("Recall: ", recall)
    print("F1 Score: ", f1)
    print("ROC AUC: ", roc_auc)

평가
pred = lr.predict(test_input)
get_clf_eval(test_target, pred)
성능이 크게 떨어지지는 않지만 아쉬운 감이 있다.

그래서 머신러닝의 국밥 그레디언트 부스팅을 이용해 다시 한번 학습시켜보았다.

그레디언트 부스팅
from sklearn.ensemble import GradientBoostingClassifier
gb = GradientBoostingClassifier(n_estimators=100, learning_rate=0.1, max_depth=3)
gb.fit(train_input, train_target)
pred = gb.predict(test_input)
get_clf_eval(test_target, pred)
로지스틱 회귀를 사용한 모델보다 성능이 개선된 모습을 보여준다.

제일 먼저 히스토그램 기반 그레디언트 부스팅을 사용해보았지만 데이터셋이 작은 탓인지 그레디언트 부스팅보다 성능이 낮은 모습을 보여주었다.

6. 결과 시각화 및 커뮤니케이션

로지스틱 모델과 그레디언트 부스팅 모델을 비교해보겠다.

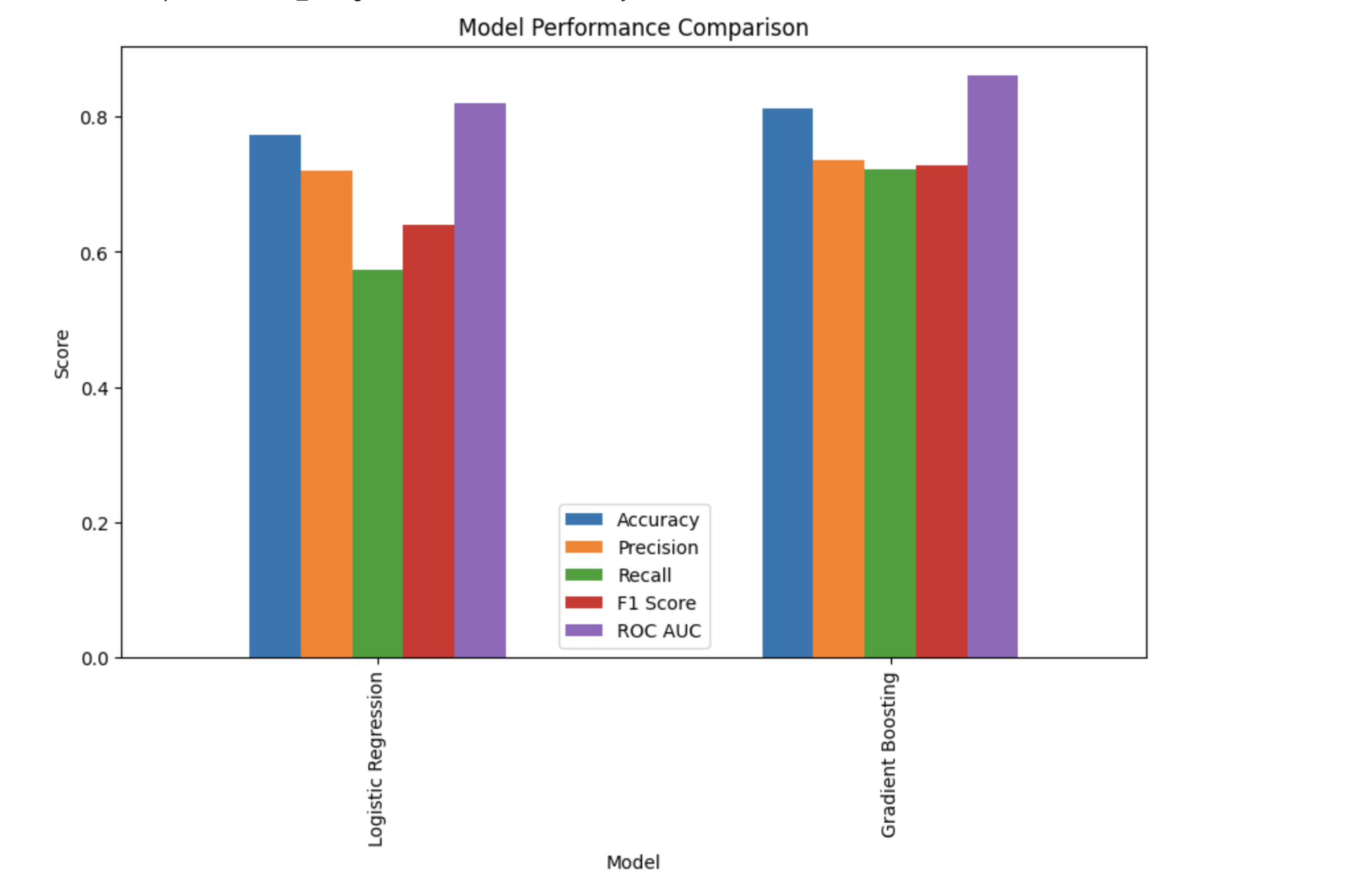
models = ['Logistic Regression', 'Gradient Boosting']
accuracy = [accuracy_score(test_target, lr.predict(test_input)), accuracy_score(test_target, gb.predict(test_input))]
precision = [precision_score(test_target, lr.predict(test_input)), precision_score(test_target, gb.predict(test_input))]
recall = [recall_score(test_target, lr.predict(test_input)), recall_score(test_target, gb.predict(test_input))]
f1 = [f1_score(test_target, lr.predict(test_input)), f1_score(test_target, gb.predict(test_input))]
roc_auc = [roc_auc_score(test_target, lr.predict_proba(test_input)[:, 1]), roc_auc_score(test_target, gb.predict_proba(test_input)[:, 1])]
metrics_df = pd.DataFrame({
    'Model': models,
    'Accuracy': accuracy,
    'Precision': precision,
    'Recall': recall,
    'F1 Score': f1,
    'ROC AUC': roc_auc
})
metrics_df.set_index('Model', inplace=True)
metrics_df.plot(kind='bar', figsize=(10, 6))
plt.title('Model Performance Comparison')
plt.ylabel('Score')
plt.show()

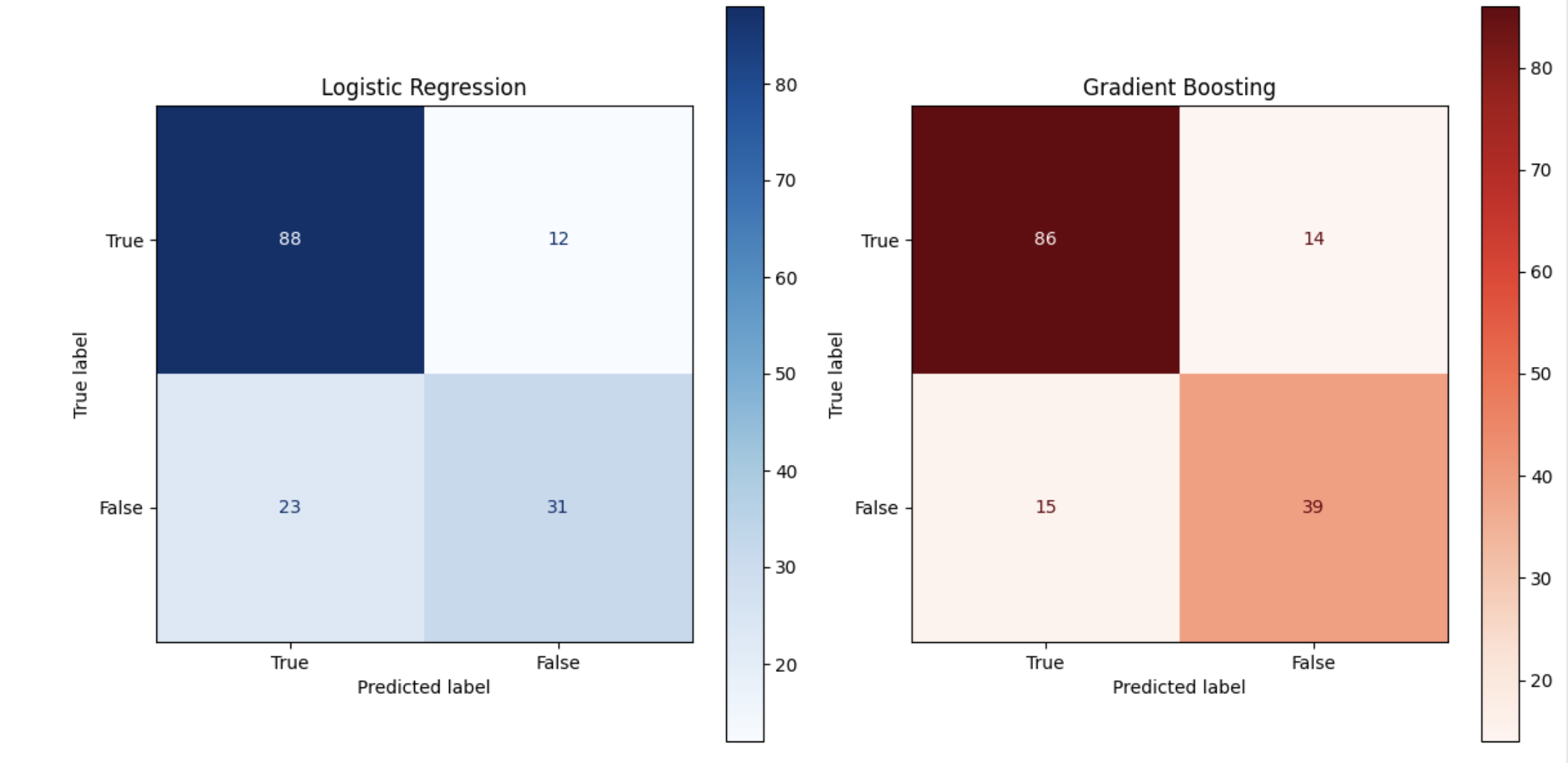
그레디언트 부스팅 모델이 전반적으로 성능이 우수하지만 특히 재현율에서 성능이 월등히 좋다는 것을 알 수 있다.

from sklearn.metrics import ConfusionMatrixDisplay
fig, axes = plt.subplots(1, 2, figsize=(12, 6))
# 로지스틱 회귀 혼동행렬 시각화한 것
cm_lr = confusion_matrix(test_target, lr.predict(test_input))
ConfusionMatrixDisplay(cm_lr, display_labels=['True', 'False']).plot(ax=axes[0], cmap='Blues')
axes[0].set_title('Logistic Regression')
# 그레디언트 부스팅 혼동행렬 시각화한 것
cm_gb = confusion_matrix(test_target, gb.predict(test_input))
ConfusionMatrixDisplay(cm_gb, display_labels=['True', 'False']).plot(ax=axes[1], cmap='Reds')
axes[1].set_title('Gradient Boosting')
plt.tight_layout()
plt.show()