[논문 리뷰]_Wasserstein GAN

코넬·2023년 12월 20일

PapersReview

목록 보기

35/35

Introduction

max_{\theta\in{R^d}}\frac{1}{m}\sum_{i=1}^mlogP_{\theta}(x^{(i)})

generative model 들은 대부분 unsupervised learning 으로, 학습 데이터 x에 대한 정답 라벨값 y 가 존재하는 것과 다르게 데이터 x의 분포 P(x)를 직접 학습합니다.

위와 같은 식을 통해 P(x) 확률 분포를 parameter $\theta$ 에 대해 표현할 수 있으며, 이를 학습시킬 수 있습니다.

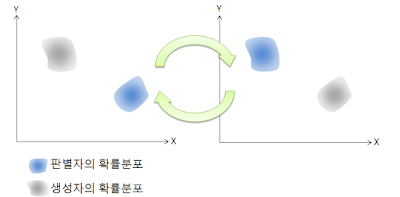
학습과정에서, P(x) 식을 직접 표현하는 것은 이미 답을 알고 있다라는 의미가 되므로 불가능하기에, GAN 에서는 x를 결정하는 latent variable z의 분포를 가정하여 입력으로 대입하고, discriminator와 generator 간의 관계를 학습시켜 generator의 분포를 P(x)에 가깝게 학습하고자 하였습니다.

GAN의 문제점

Generative adversarial network 의 문제점은 discriminator 와 generator 간의 균형을 유지하여 학습하기 힘들고 (균형을 맞추기 힘들고), 학습이 완료된 이후에도 mode dropping 이 발생한다는 점입니다.

이는 discriminator 가 teacher 의 역할을 해주지 못해 모델이 최적화 지점까지 도달하지 못했기 때문이죠 !

mode collapsing

mode collapsing 설명

GAN은 패턴을 만들어내는 문제를 Minimax Game 으로 접근한다고 했습니다. 이미 설명했듯이 Minimax Game은 최악(최대 손실)의 상황에서 손실을 최소화하는 게임입니다. 그리고 GAN에서의 최악의 상황은 판별자가 진짜 데이터의 분포를 완벽히 학습한 상태입니다. 그러나 여기서 모순이 생깁니다. 학습을 마치기 전에는 완벽한 판별자를 얻을 수 없기때문에, GAN이 해결하는 문제가 Minimax Game 이라는 가정이 애초에 성립하지 않는 것이죠.
GAN의 학습 과정에서 모델이 수렴하지 않거나 진동하는 이유 중의 하나가 바로 이것입니다. 판별자가 안정적으로 최적해로 수렴한다면 문제가 없지만, 그렇지 않을 경우 생성자도 최적의 해로 수렴하지 않는 것은 당연한 일입니다. 생성자를 지도하는 '선생님'의 역할을 하는 판별자의 능력이 떨어지면 생성자의 능력도 떨어질 수 밖에 없습니다.

GAN의 학습 과정에서 판별자와 생성자를 번갈아가며 학습시킨다고 설명했습니다. 이때문에 또 다른 문제가 발생할 수 있습니다. 특정 학습 이터레이션에서 판별자의 학습과 생성자의 학습이 서로를 상쇄할 수 있다는 말입니다. 이를 데이터 분포의 측면에서 그림으로 단순화하면 다음과 같습니다.

판별자와 생성자가 서로를 속고 속이며 제자리를 맴돈다면 양쪽 모두 전역해로 수렴할 수 없게 됩니다. 이런 상황을 일컬어 모델이 진동(oscillation)한다고 합니다.

위와 같은 문제점이 합쳐져서 나오는 현상이 mode collapsing 입니다. 여기서 mode는, 통계학에서 나오는 단어로 최빈값 (빈도가 가장 높은 값)을 뜻합니다.
데이터의 확률밀도함수에서는 색이 가장 진한 부분인 밀도가 가장 높은 부분을 뜻하죠.

multi-modal은 mode가 여러개 존재하는 경우로, MNIST 를 예로 들면 숫자 10개가 mode 에 해당됩니다. 0~3 사이의 숫자 네개가 존재한다고 하면, MNIST 데이터의 분포는 다음과 같이 나타낼 수 있습니다.

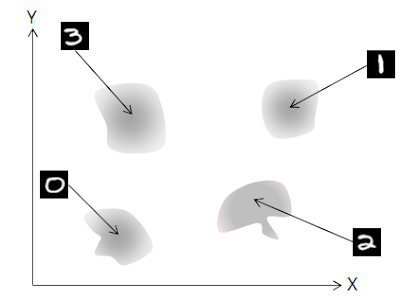
위의 그래프는 mode가 여러개인 분포입니다.
문제는 생성자가 주어진 입력을 네개의 mode 중 하나로만 치우쳐서 변환시킬 때 벌어집니다.

말그대로 mode의 충돌, mode collapsing 이 발생한 것입니다.

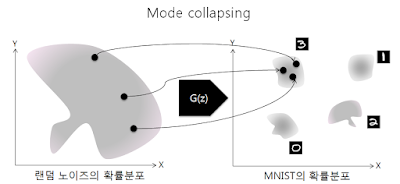
실제로 MNIST 데이터세트를 이용하여 GAN을 학습시키다 보면 같은 숫자만 계속해서 생성되는 현상을 볼 수 있는데, 이것이 바로 mode collapsing이 발생한 것입니다. 생성자 입장에서는 어떤 숫자를 만들든 판별자만 속이면 되기때문에 게임의 목적은 달성했다고 말할 수 있고, 판별자 입장에서도 잘못된 판단이라고 말할 수 없습니다.
이러한 현상은 위에서 언급했듯이 판별자가 완벽하지 못하거나, 모델이 진동할 때, 혹은 두가지 문제점이 동시에 발생하는 경우 심하게 나타납니다. 생성자가 '0'만 계속 생성하다가 판별자가 진동하면서 '1'의 분포로 이동하면, 생성자는 다시 '1'만 계속해서 생성합니다. 그리고 이러한 악순환이 다른 숫자들에 대해서 반복되는 것이죠. 결과적으로 생성자가 학습 데이터 전체의 분포를 학습하지 못하고 그 중 일부분만 배우게 되는 것입니다. 아래 그림에서 그 예를 볼 수 있습니다.

결국 생성자와 판별자 사이의 능력에 적절한 균형을 이루면서, 두 네트워크가 안정적으로 전역해로 수렴하도록 만드는 것이 GAN이 해결해야 할 숙제가 되는 것이죠.

Points of Wasserstein GAN

Wasserstein GAN 에서는 기존의 GAN 과 다르게 다음과 같은 제안을 하고 있습니다.

discriminator 의 학습 방식은 동일하나 loss를 대체할 critic을 사용합니다. (기존의 discriminator는 판별을 위해 sigmoid 를 사용하고, output값은 가짜와 진짜에 대한 예측 확률 값을 뱉어냅니다.)
반면에 cirtic 은 EM(Earth Mover) distance로부터 얻은 scalar 값을 이용합니다.
EM distance는 확률 분포 간의 거리를 측정하는 척도 중 하나로, 일반적으로 사용된 척도는 KL divergence입니다. KL divergence는 매우 엄격히 거리를 측정하는 방법이기에, continuous 하지 않은 경우가 있으며, 학습시키기 어려워 EM distance를 대신 사용합니다.

Different Distances

확률 거리 척도를 다른 방식으로 바꿔 사용하는 이유와, 그 종류에 대해 설명하고 있습니다.
더욱 자세한 방식은 다음과 같은 슬라이드를 참고하면 훨씬 더 쉽게 이해할 수 있습니다.

Example 1

랜덤 변수 Z: 이것은 구간 [0, 1]에서 균일 분포를 따르는 연속적인 랜덤 변수입니다. 수학적으로는 Z∼U[0,1]로 나타낼 수 있습니다.
분포 $P_0$ : 이 분포는 카테시안 평면 $\mathbb{R}^2$ 상에 정의되어 있습니다. 균일 분포 Z에서 각 샘플 z에 대해 점 (0,z)이 생성됩니다. 이는 x-좌표가 항상 0인(x축 위에 있는) 점이며, y-좌표는 Z에서 샘플링된 값입니다. 다시 말하면, $P_0$ 는 원점을 지나는 수직선 상에서 균일합니다.
변환 함수 $g_0(z)$ : 이 함수는 매개변수 θ와 랜덤 변수 Z에서의 값 z를 가져와서 $\mathbb{R}^2$ 상의 점을 반환합니다. 이는 점을 수평으로 매개변수 θ만큼 이동시키는 것으로 이해할 수 있습니다.
수학적으로는 $g_0(z)=(θ,z)$ 로 표현됩니다.

요약하면, 구간 [0, 1]에서 균일하게 분포된 랜덤 변수 Z, 해당 Z의 샘플을 이용하여 정의된 수직선 상의 분포 $P_0$ , 그리고 매개변수 θ에 따라 이 점을 수평으로 이동시키는 변환 함수 $g_0(z)$ 가 있다고 예를 들어봅시다. 이러한 경우에 ,

Total Variation (TV)

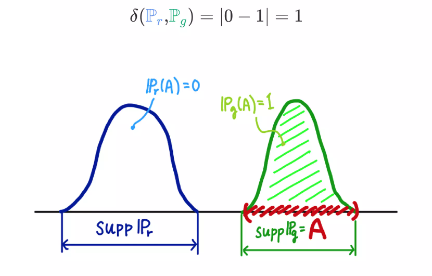
Total Variation 은 두 확률측도의 측정값이 벌어질 수 있는 값 중 가장 큰 값을 의미합니다.
( Supremum : the least upper bound 로, 상한(upper bound)에서 가장 작은 값(minimum)을 뜻합니다. )

같은 집합 A이더라도 두 확률분포가 측정하는 값은 다를 수 있는데, TV는 모든 $A \in \sum$ 에 대해 가장 큰 값을 거리로 정의합니다.

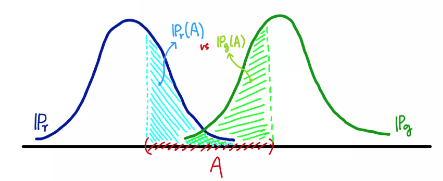
만약의 두 확률분포의 확률밀도함수가 서로 겹치지 않는다면, 확률 분포의 support의 교집합이 공집합이라면 TV는 무조건 1이 됩니다.

Kullback - Leibler Divergence & Jensen-Shannon (JS) divergence

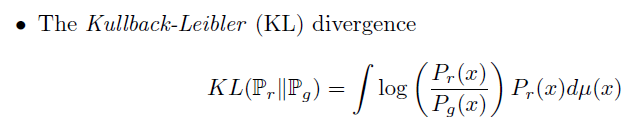
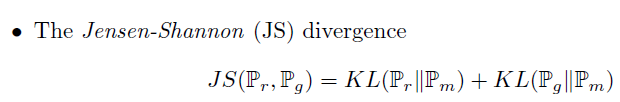
KL 은 metric 이 아닙니다. 대칭성과 삼각부등식이 깨지기 때문입니다. 하지만 KL 은 premetric 이기 때문에, 다음과 같은 특징을 지니고 있습니다.

여기서 $\mathbb{P}_r$ 과 $\mathbb{P}_g$ 는 겹치지 않습니다. 즉 $\theta \neq 0$ 인 경우,

\begin{cases}P_0(x) \neq 0 \Rightarrow P_{\theta}(x) = 0 \\ P_{\theta}(x) \neq 0 \Rightarrow P_0(x) = 0 \end{cases}

가 됩니다. 따라서 $\mathbb{P}_{\theta} > 0$ 인 곳에서 log의 값은 $\infty$ 가 됩니다.

위와 같이 계산한 log 의 값이 특정 값으로 수렴하거나 발산하는 이유는 TV나 KL 이나 JS는 두 확률분포 $\mathbb{P}_r$ 과 $\mathbb{P}_g$ 가 서로 다른 영역에서 측정된 경우, 완전히 다르다 라고 판단을 내리게끔 metric 이 계산되기 때문입니다.

즉 두 확률분포의 차이를 매우 strict하게 본다는 뜻이죠.

이러한 측정방식이 다른 model 의 경우에는 유리할 수 있지만, GAN 의 경우에는 discriminator의 학습이 잘 죽는 원인이 됩니다. 따라서 GAN의 학습에 맞게 유연하면서도 수렴에 focus 를 맞춘 다른 metric 이 필요하게 됩니다.

Earth-Mover (EM) distance or Wasserstein-1

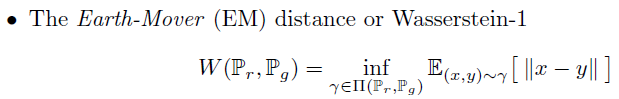
Earth-Mover를 활용한 Wasserstein distance 정의는 위와 같습니다.

여기서 $\gamma \in \prod(\mathbb{P}_r, \mathbb{Q}_g)$ 는 두 확률분포 $\mathbb{P}_r, \mathbb{Q}_g$ 의 결합확률분포(joint distribution)를 모은 집합이며, 여기서 $\gamma$ 는 그 중 하나입니다.

위 식은 모든 결합확률분포 $\prod(\mathbb{P}_r, \mathbb{Q}_g)$ 중 d(X,Y) 의 기댓값을 가장 작게 추정한 값 을 의미합니다.

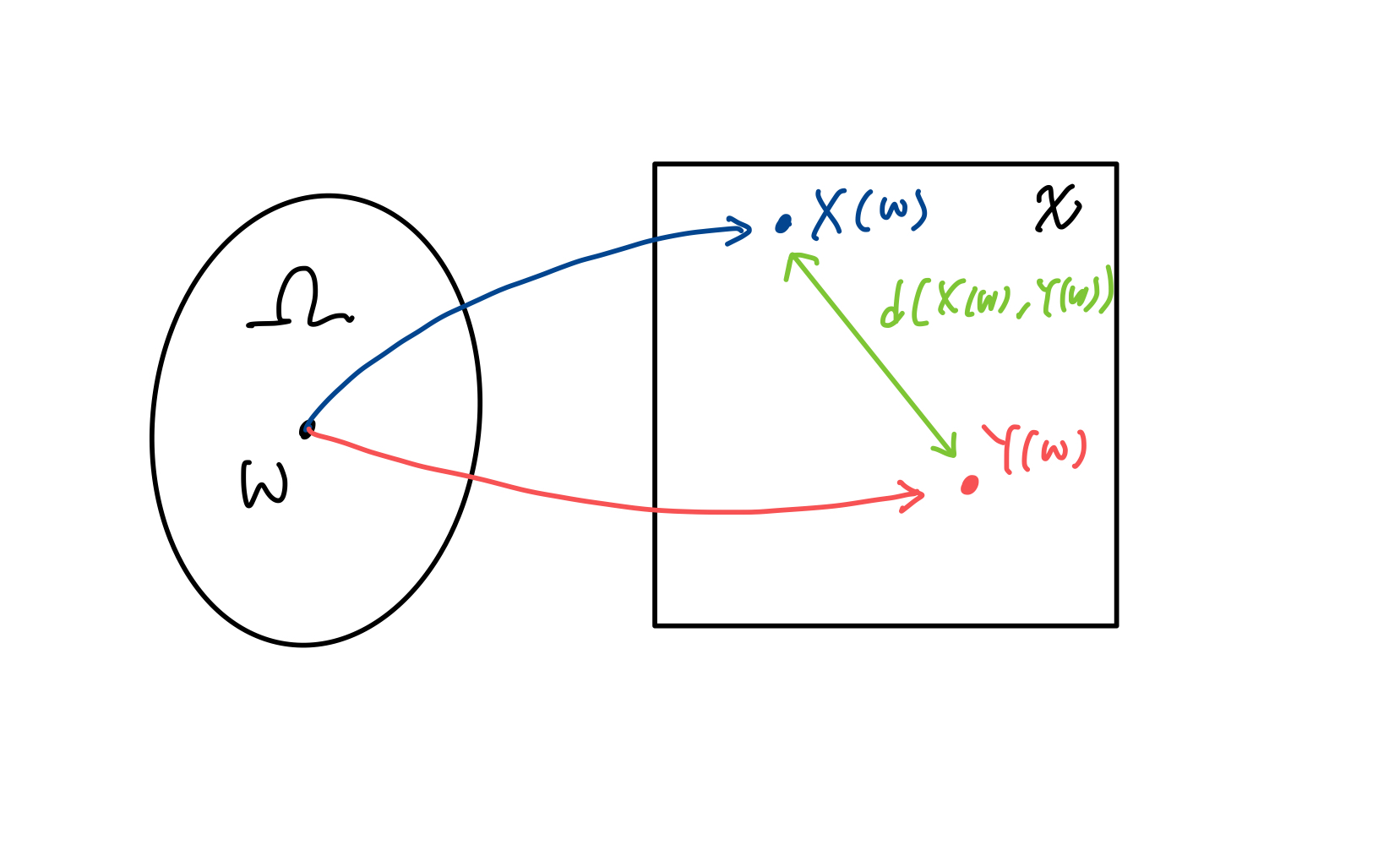
예를 들어, w 하나를 샘플링(추출) 하면 X(w)와 Y(w)를 뽑을 수 있습니다. 이 때 두 점간의 거리인 d(X(w), Y(w))를 계산할 수 있습니다.

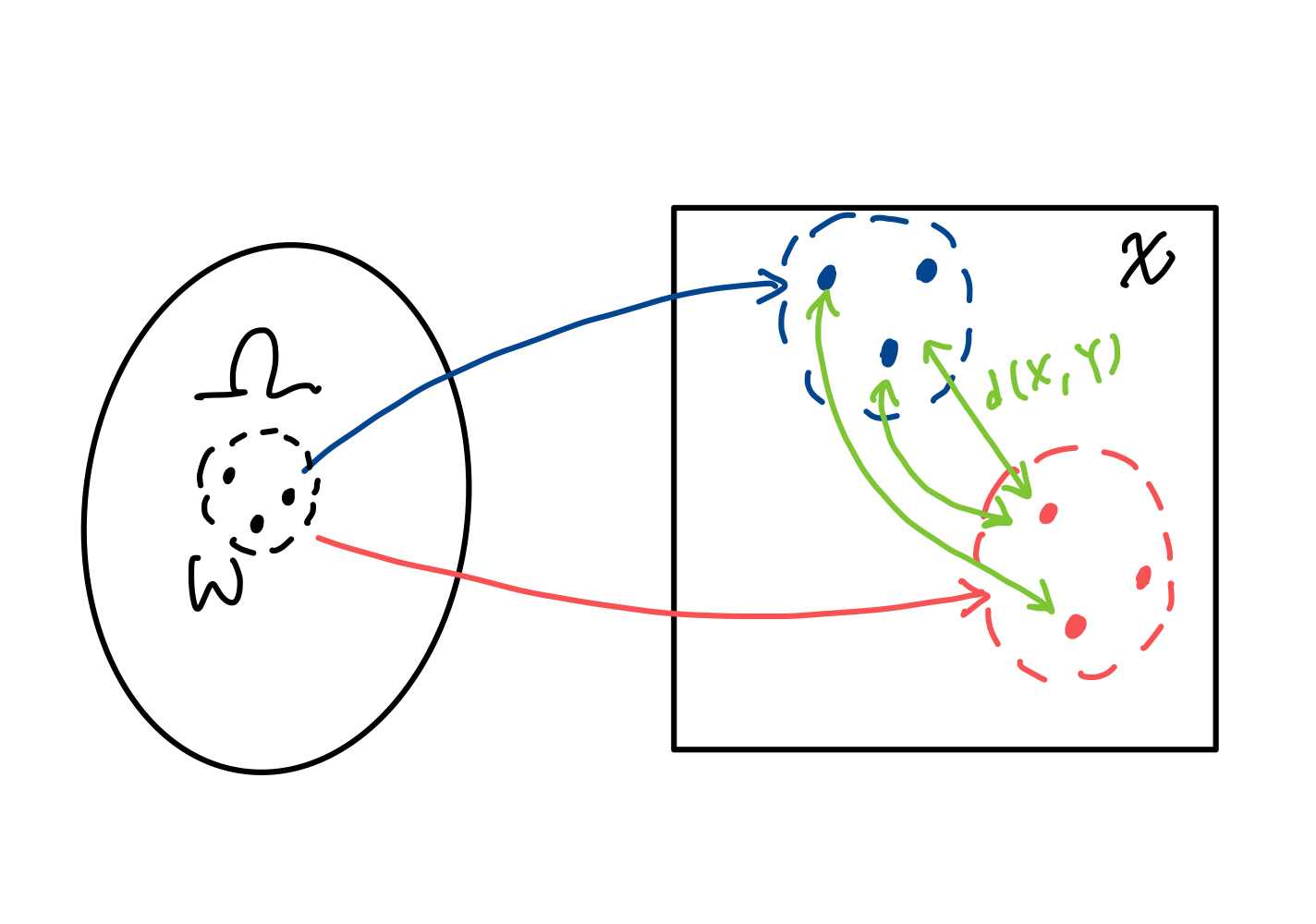
샘플링을 계속 할수록, (X,Y)의 결합확률분포 $\gamma$ 의 윤곽이 나오게 되고, 더불어 $(\mathbb{P}, \mathbb{Q})$ 는 $\gamma$ 의 주변확률분포 가 됩니다.

감마가 두 확률변수 X,Y의 연관성을 어떻게 측정하느냐에 따라, d(X,Y)의 분포가 달라지게되는데요,

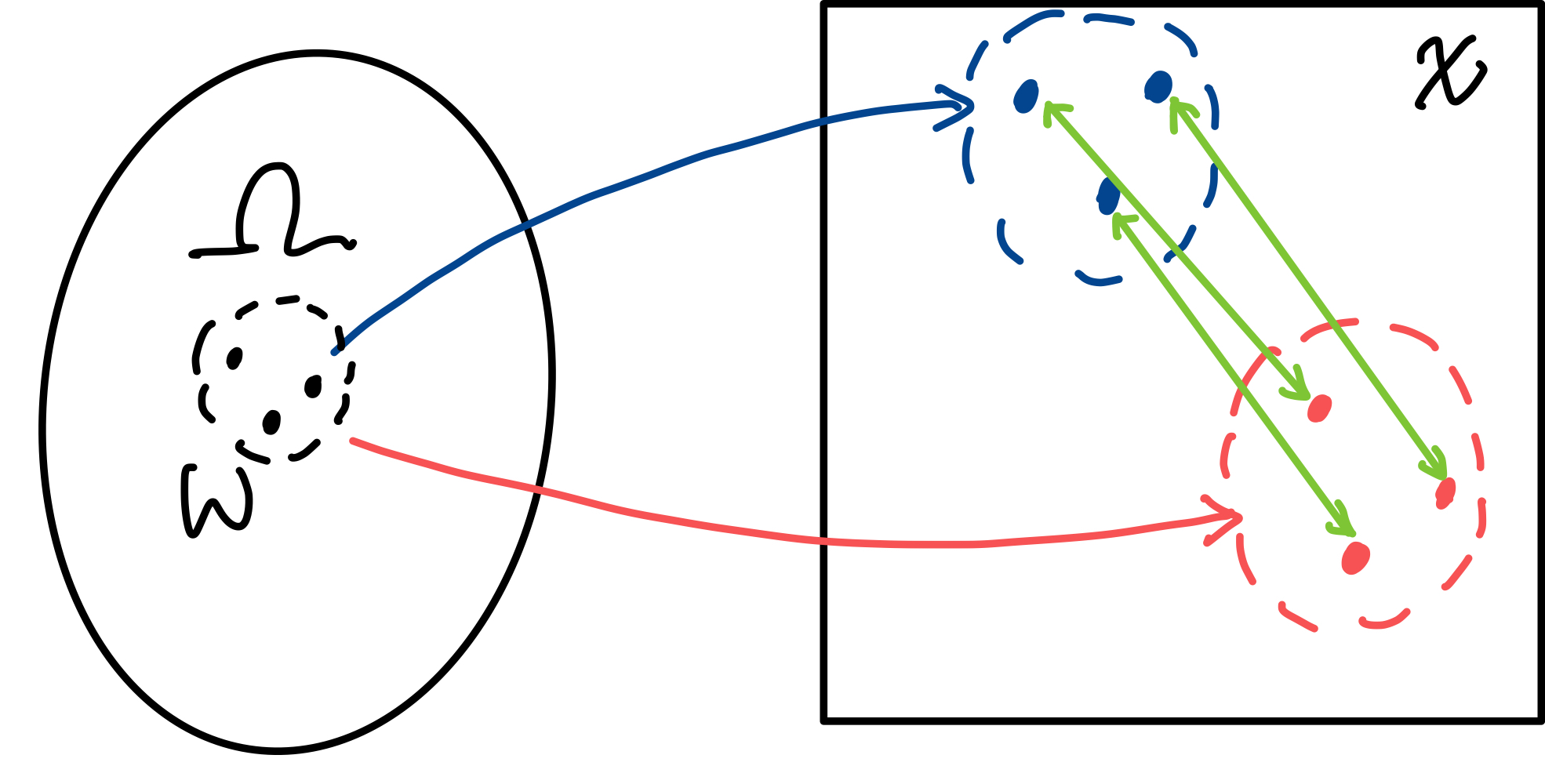
여기서 wasserstein distance는 여러가지 $\gamma$ 중에서 d(X,Y) 의 기대값이 가장 작게 나오는 확률분포를 취하게 됩니다.

이를 example 1에 대입하여 생각해보면, 두 확률변수 (X,Y)가 각각 w에 대해 2차원 공간인

X(w) = (0,Z_1(w)), Y(w) = (\theta, Z_2(w))

으로 매핑됩니다.

이 때, 두 점 사이의 거리는

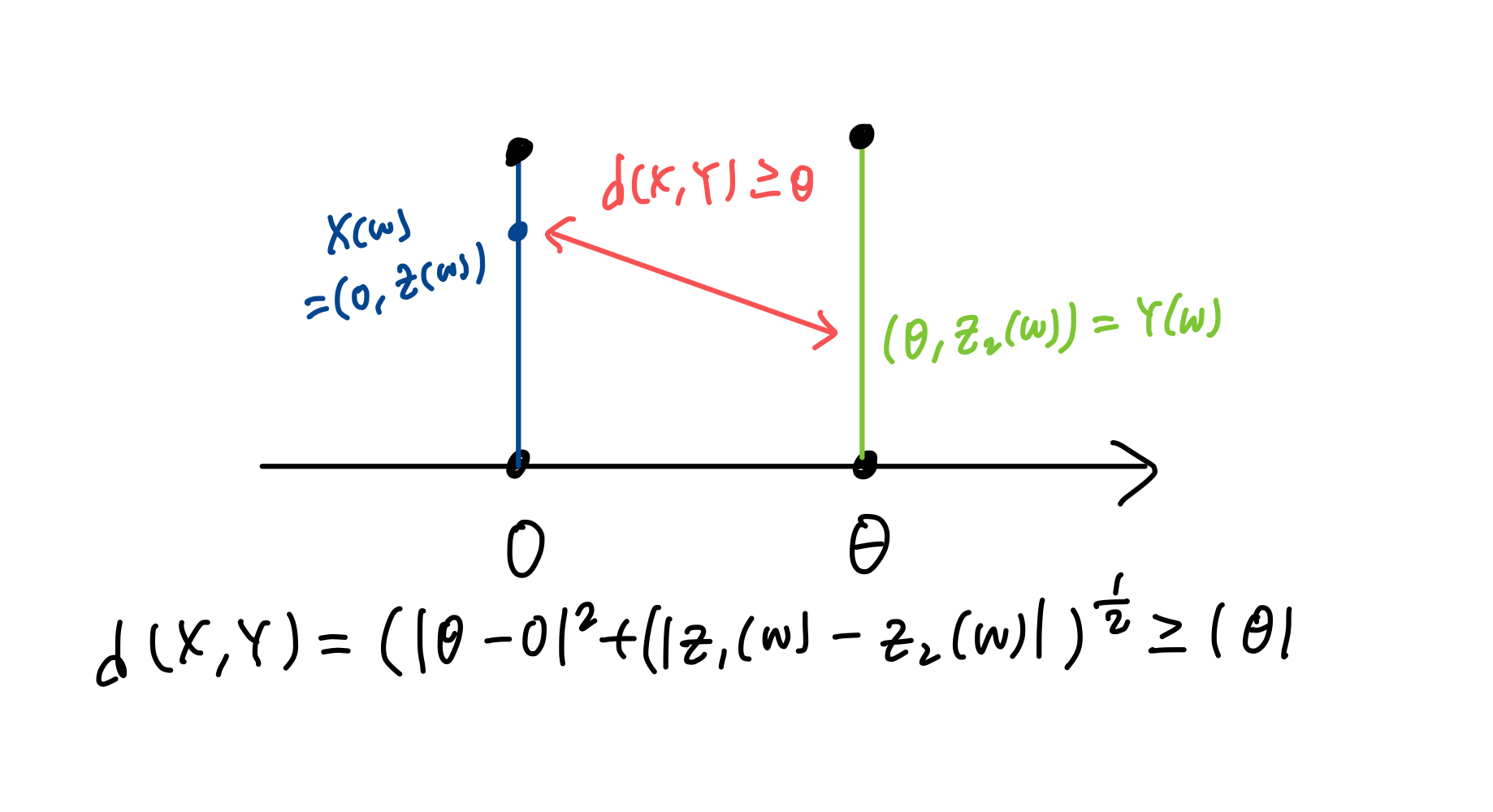
이와 같이 계산이 됩니다. 즉 d(X,Y)의 기대값은 어떤 결합확률분포 $\gamma$ 를 사용하든 항상 $|\theta|$ 보다 크거나 같게됩니다.

\mathbb{E}^{\gamma}[d(X,Y)] \ge \mathbb{E}^{\gamma}[|\theta|] = |\theta|

그렇다면 기대값이 $|\theta|$ 인 상황이 존재할까요?
그 조건은 항상 $Z_1 = Z_2$ 인 분포를 따른다면 가능하게됩니다.

이렇게 이상적인 수렴값을 얻는 방식이 wasserstein distance의 정의입니다.

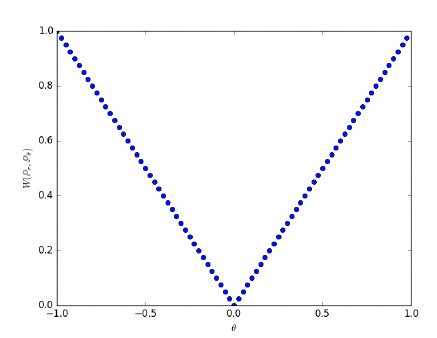
수학적 정리

TV, KL, JS 는 $(\mathbb{P}_r,\mathbb{P}_g)$ 가 서로 겹치지 않는 상황에서는 불연속이 됩니다.
EM은 TV, KL, JS보다 약한 metric으로 수렴을 판정하는데 soft한 성질을 지닙니다.
EM은 분포수렴과 동등합니다.

분포 수렴이란?
분포 수렴은 확률분포 수렴 종류 중 하나로 가장 약한 수렴입니다.
확률 분포의 개별적인 특징보다, 전체적인 모양을 중시하는 수렴으로, 중심극한정리 에서 표본평균이 정규분포로 수렴하는 종류가 분포수렴이라고 합니다.

Wasserstein distance는 Optimal transport 분야에서 매우 중요하게 다뤄지는 개념으로, transport cost minimization 문제와 관련있습니다.

즉, 두 공간을 어떻게 연결시켰을 때 가장 최적인 경로를 찾을 수 있는지 결정할 수 있는 수학 문제와 관련이 있다고합니다.

Theorem 1. EM distance를 사용하기 위한 제약조건

EM distance를 loss function으로 사용하기 위해서는 미분이 가능해야합니다.

$P_r$ 은 학습하고자 하는 목표 distribution이며, $P_θ$ 는 학습시키고 있는 현재의 distribution으로 가정합니다.

z는 latent variable의 space이며, 함수 g는 latent variable z를 x로 mapping하는 함수입니다. 이 때 $g_θ(z)$ 의 distribution이 $P_θ$ 가 됩니다.

이 때,

g가 θ에 대해 연속한다면, Pr와 Pθ의 EM distance 또한 연속합니다.
g가 Lipschitz조건을 만족한다면, Pr와 Pθ의 EM distance 또한 연속합니다.

여기서 Lipschitz조건 이란, 두 점 사이의 거리를 일정 비 이상으로 증가시키지 않는 함수를 뜻합니다.

|f(x_1) - f(x_2)| \le K|x_1-x_2|

위의 식이 K-Lipschitz 조건이며, 이 조건을 만족하기 위하여 clipping 을 진행합니다.

Wasserstein GAN

Wasserstein GAN 에서 Wasserstein Divergence 는 Earth-Mover(EM) Distance 바탕으로 측정됩니다.

따라서 계산해야 할 Loss function 도 EM distance를 계산해야하는데, 이 부분에서 inf 같은 경우, $P_r$ 과 $P_g$ 의 joint distribution을 계산해야 확인할 수 있는데, $P_r$ 이 목표 대상이기 때문에 알 수 없게됩니다.

따라서 Kantorovich-Rubinstein duality를 이용하여 식을 변환하면

여기서 $||f||_L \le 1$ 의 의미는 f 가 1-립시츠 조건을 만족한다는 의미입니다.

이를 학습시키기 위해서 parameter 가 추가된 f 로 수식을 바꾸고, Pθ 를 g(θ) 에 대한 식으로 바꾸면 다음과 같은 수식이 됩니다.

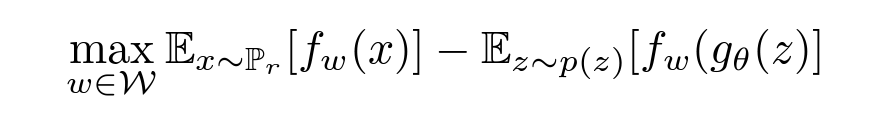
이와 같은 모습이 기존의 GAN loss 와 비슷한 모습임을 확인할 수 있습니다.

논문의 이 부분에서 $P_r$ 이 여전히 존재하는데도 알맞은 loss 인 이유를 확인할 수 있는데요, 앞부분은 잘 학습된 discriminator, 즉 critic 이 $P_r$ 의 역할을 해주고, 위와 같이 gradient 를 update 할 때에는 θ에 대해 미분하면 앞 항이 사라져 계산이 가능합니다.

f(x)는 Lipschitz 조건을 만족하는 함수이므로, discriminator 역할을 하는 함수입니다. (critic 이라고 부르죠 !)

critic의 loss function 항 자체가 EM distance(Wasserstein distance)를 의미하므로, 위 loss function을 최대화하는 함수 f를 찾는 문제가 됩니다. 여기서 w는 함수 f의 parameter, 즉 critic의 parameter이며, maximize이므로 w에 대한 gradient descent입니다.

최대화 이유?
Kantorovich-Rubinstein duality를 통해 sup으로 변형되고, 이후parameter 식으로 변형하면서 maximize로 바뀌게됩니다.

generator의 loss function역시 Theorem3에서 정의한 대로, 변형한 Wasserstein distance 식을 θ 에 대해 미분하여 앞의 식을 사라지게 하면 얻을 수 있다. generator의 경우, Theorem3에서 미분 결과에서 볼 수 있듯이 앞에 - 가 붙어있다!! 즉, θ에 대한 gradient descent이다.

Algorithms

WGAN 의 학습 알고리즘을 확인해봅시다.

먼저 n critic번 만큼 critic을 학습시키는 부분이 있는데요,

$P_r$ 과 p(z) ( $P_θ$ 역할)를 미니배치만큼 샘플링한 후에, critic의 loss function을 이용하여 parameter w (즉 함수 f)를 update합니다.

여기서 update 후 clip(w, -c, c) 라는 부분이 있는데, Lipschitz조건을 만족하도록 parameter w가 [-c, c]공간에 안쪽에 존재하도록 강제하는 과정입니다.

이를 Weight clipping 이라고 합니다.

이는 WGAN의 한계점이라고 할 수 있는데, 실험 결과 clipping parameter c 가 크면 limit(c나 -c)까지 도달하는 시간이 오래 걸리기 때문에, optimal 지점까지 학습하는 데 시간이 오래 걸렸다 라고 이야기합니다.

반면 c가 작으면, gradient vanish 문제가 발생합니다.

이미 간결하고 성능이 좋기 때문에 사용하였지만, 이후의 발전된 방법으로 Lipschitz조건을 만족시키는 것은 다른 학자들에게 맡긴다 라고 작성되어있네요 🤣

Discriminator & Critic
discriminator의 경우 일반적인 분류 neural net과 같이 이미지가 진짜인지, 가짜인지 sigmoid확률값으로 판별해 냅니다.

반면에 critic의 경우, Wasserstein GAN 식 자체를 사용하기 때문에, scalar 값이 output이 됩니다.
이는 이미지가 진짜인지 아닌지에 대한 점수를 의미하는 것으로, sigmoid와 달리 saturation현상이 없고 좋은 gradient를 만들 수 있습니다.

따라서 진짜 optimal 지점까지 쉽게 학습이 가능하고, 앞에서 언급했던

discriminator와 generator간의 balance 맞추기

mode dropping (mode collapse) 문제
두 가지를 해결 할 수 있게 되지요 !

Adam 을 사용 안하고 RMSProp 를 사용하는 이유?

실험 결과 critic을 학습 할 때 Adam과 같은 mometum 베이스 optimizer를 사용하면 학습이 unstable 한 이유 떄문인데요,

이유는, loss값이 튀고 샘플이 좋지 않은 경우(일반적으로 학습 초반) Adam이 가고자 하는 방향, 즉 이전에 기억했던 방향(Adam step)과 gradient의 방향 간의 cosine값이 음수가 됩니다.
일반적으로 nonstationary 문제(극한값이 존재하지 않음)에 대해서는 momentum계열보다 RMSProp이 성능이 더 좋다고 한다.(여기서 정의한 문제도 nonstationary problem)

Results

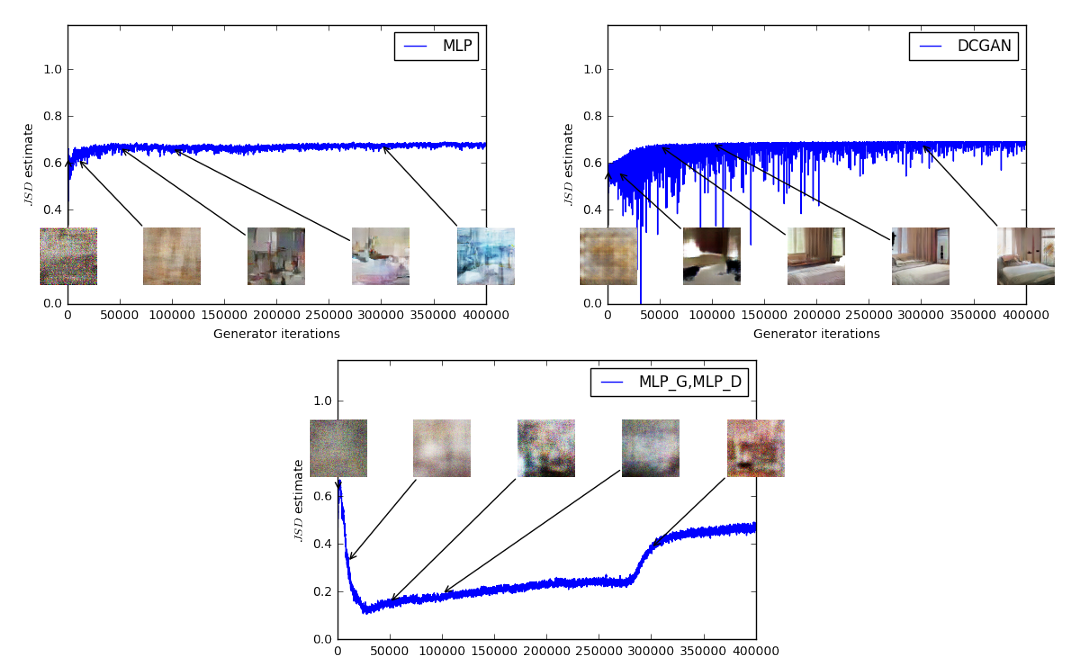
맨 위의 그래프들은 discriminator 대신에 critic을 적용한 것이고, 왼쪽은 generator로 Multi Layer Perceptron, 오른쪽은 DCGAN을 이용한 결과입니다.

sigmoid를 (기존 discriminator를) 사용하지 않아 wasserstein 거리가 점차적으로 줄어들고, sample의 결과도 훨씬 좋아진 것을 볼 수 있습니다.

아래 그림은 discriminator와 generator모두 MLP를 사용한 결과입니다. Sample 그림은 무엇인지 알아보기 어렵고, 각 sample에 대해 wasserstein distance 를 계산하여 보았을 때 상수값으로 변화하지 않는 것을 볼 수 있습니다.