AlexNet : ImageNet Classification with Deep Convolutional Neural Networks

AlexNet에서 CNN의 사용 이유

엄청난 양의 클래스를 이미지들로부터 학습시키기 위해서는 객체 탐지에서의 복잡성을 해결해야 하는데, 방대한 양의 데이터셋만으로는 부족 → 모델 자체도 방대한 양의 사전 지식을 가지고 있어야한다. 이를 해결하기 이해 등장한 모델 .

CNN의 경우, depth 와 width 를 조절하여 모델의 크기 조정이 가능하며, 이미지 본질에 대해 강한 추측이 가능하다. → 기존의 비슷한 크기의 신경망에 비해 CNN 이 더 적은 connection 과 parameter로 훈련 가능 & 더 좋은 효과를 나타낸다.

AlexNet은 5개의 conv layer 와 3개의 FC layer로 구성되어있으며, 온전해야한다.

사용한 데이터셋

ImageNet : 22,000 카테고리에 대한 1500만개의 이미지를 제공한다. 이미지넷에서 제공하는 이미지 크기가 다양한데, 알렉스넷의 경우에는 256 X 256 으로 고정된 이미지를 input으로 넣는다. 따라서 이미지 전처리 과정이 필요하다. 이미지를 downscale 해주는데, 우선적으로 이미지의 최소 부분을 256이 되도록 rescale, 256 X 256 사이즈로 중앙에서부터 crop 진행하였다.

신경망 구조

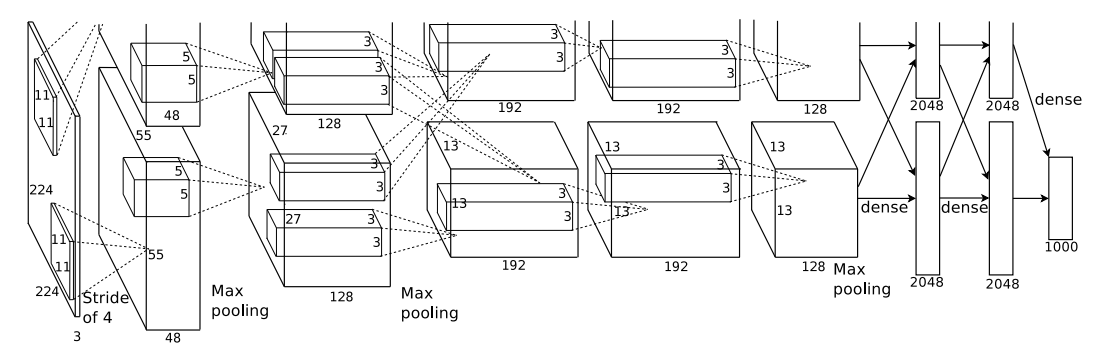
총 8개의 레이어로 구성, 5개가 conv layer이고 3개가 FC layer 이다. 마지막 FC layer 층에서는 softmax를 사용하여 1000개의 output을 출력한다.

2,4,5번째 conv layer 에는 이전 layer에서 같은 GPU 에 존재하는 kernel map에서만 input을 받아들인다.

3번째 conv layer 에서는 모든 kernel map들로부터 input 값을 받아들인다. FC layer 의 뉴런들은 이전 레이어의 모든 뉴런들과 연결되어있다.

1. Response Normalization layer(LRN) 이 첫 번째와 두 번째 layer 다음에 연결
2. Max Pooling layer 도 LRN layer 다음과 5번째 layer 에도 연결
3. Conv layer 와 FC layer 모두 ReLU 활성화함수 사용

ReLU Nonlinearity

입력 x에 대해 f를 출력하는 기본적인 방법의 경우 f(x) = tanh(x) 혹은 f(x) = (1+e^(-x))^(-1) 인데, 경사하강법을 이용한 훈련 시간에서는 f(x) = max(0,x) 보다 느리다. CNN 구조 에서의 ReLU의 경우 기본적인 방법보다는 몇배는 빠르다. 또한 에러율도 ReLU를 이용한 4개의 CNN 층만으로도 6번 epoch 만에 에러율을 줄이는 모습을 확인할 수 있다.

Local Response Normalization

ReLU를 사용하면 포화상태에 대해서 정규화 과정이 없어도 발생시키는 것을 막을 수 있으나, ReLU의 특성상 한 뉴런의 값이 엄청나게 커질 경우, 다른 뉴런에게 영향을 끼칠 수 있는데, 이 현상을 억제하고자 LRN이 나오게 되었다. 현재는 batch normalization이 더 자주 쓰인다.

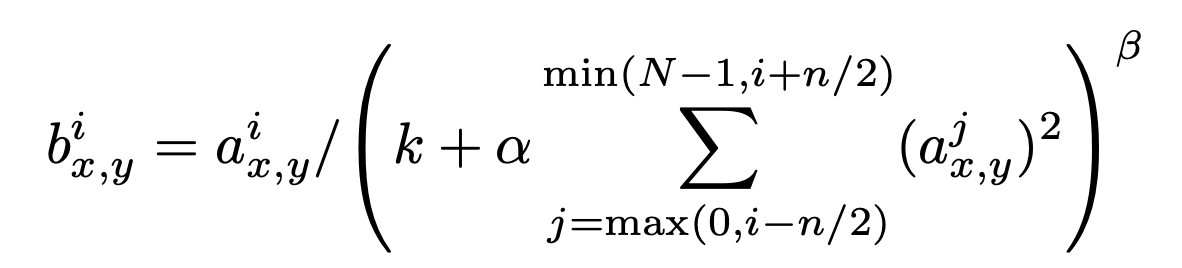
• a^i_x,y :(x,y) 에 위치한 픽셀에 i 번째 커널을 적용, ReLU를 사용했을 때 나온 활성화 값
• n : 인접하다고 고려할 뉴런의 개수
• N : layer 안에 존재하는 kernel의 총 개수

과적합을 막는 방법

Data Augmentation 진행

데이터 증강이라고 한다. GPU에서 이전 배치에 대한 학습을 진행중 일 때, CPU 에서 다음 training set 준비를 위해 진행한다. 증강을 위한 변형 과정은 이동, 좌우반전인데, 256 256 사이즈의 이미지에서 랜덤으로 224 224 크기의 patch 를 잘라내고, test에서는 224 * 224 의 patch 들을 horizontal flip 하여 10개의 patch 로 만들어낸다. 각 패치들에 대해서는 softmax 결과를 평균하여 prediction을 진행한다.

다른 변형 과정으로는 훈련 데이터의 RGB 채널의 세기 조절을 하여 데이터를 증강시키는 과정이다. 훈련 세트 RGB 값에 PCA를 수행하여

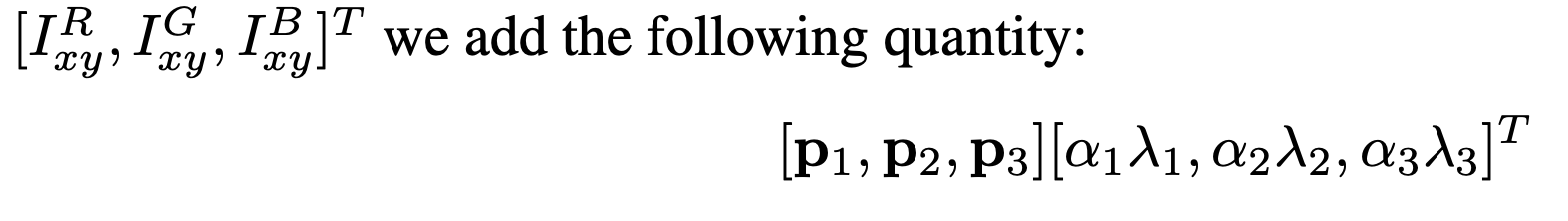
각 픽셀 값에 가우시안값에 비례하는 크기의 랜덤 변수와 이미지에서 발견된 주요 구성 요소의 배수를 더한다.

Dropout 수행하기

Dropout은 서로 연결된 연결망(layer)에서 0부터 1 사이의 확률로 뉴런을 제거(drop)하는 방법이다. 아래의 그림 1 과 같이 dropout rate가 0.5라고 가정하면, Drop-out 이전에 4개의 뉴런끼리 모두 연결되어 있는 전결합 계층(Fully Connected Layer)에서 4개의 뉴런 각각은 0.5의 확률로 제거될지 말지 랜덤하게 결정된다. 위의 예시에서는 2개가 제거된 것을 알 수 있다. 즉, 꺼지는 뉴런의 종류와 개수는 오로지 랜덤하게 dropout rate에 따라 결정된다. Dropout Rate는 하이퍼파라미터이며 일반적으로 0.5로 설정합니다.

Details of learning

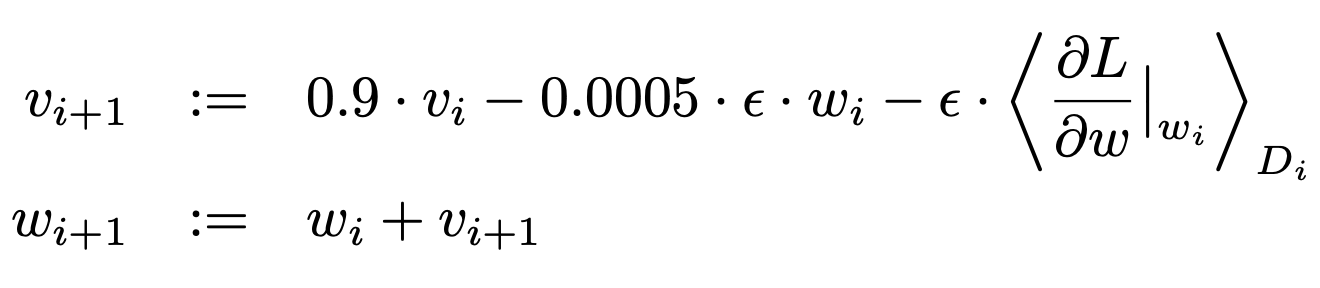
가중치 w 에 대한 업데이트는 위의 식과 같이 진행된다. (i : 반복 횟수, v : 모멘텀 변수, e: 학습률, <dl/dw>식 : i 번째 배치에서 W_i를 사용하여 구한 gradient의 평균)

최종 결과물

• 물체가 꼭 중앙에 있지 않더라도 위치에 상관없이 분류를 잘 한다.
• 픽셀 단위로 분류하는 것이 아닌, 고차원적인 원리를 통해 분류한다는 것을 확인할 수 있다.
• CNN이 방대한 데이터셋을 분류하는데 있어 비지도 학습만으로 뛰어난 성과를 보였으며, conv layer 중 한개라도 빠지면 학습 능력이 떨어지기에 깊이의 중요성을 확인할 수 있다.
• alexnet은 deep neural network의 첫 사례로, CNN을 사용하였던 점에서 의미가 깊다.
  정리하자면 다음과 같습니다.

알렉스넷의 의미

• AlexNet은 ILSVRC 대회에서 최초로 쓰인 CNN 구조이다.
• 2012년 다른 얕은 층 구조에 비해 AlexNet은 8개의 층으로 구성되어있다.
• ReLU 함수를 처음으로 Activation function으로 이용한 사례이다.
• GPU 용량 제한으로 인해 대규모 데이터셋에 문제가 있어 GPU 두 개를 사용하였다. 이를 병렬적으로 연산하여 속도와 정확도를 높였다.
• 정확도가 이전 대회 우승자에 비해 획기적으로 올랐다.